Inwendig product

Het inwendig product (ook wel inproduct of scalair product genoemd) van twee vectoren is een scalair (dus het levert een getal op). Het is een begrip uit de lineaire algebra, maar ook in andere takken van de wiskunde wordt hier veel gebruik van gemaakt. De bekendste vorm komt uit de euclidische meetkunde en is voor de vectoren $\mathbf {u}$ en $\mathbf {v}$ gedefinieerd als:

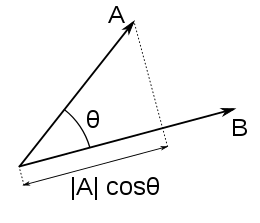
\mathbf {u} \cdot \mathbf {v} =|\mathbf {u} ||\mathbf {v} |\cos \theta

Meetkundige betekenis voor het geval van een scherpe hoek: inwendig product A.B = lengte van B × lengte van projectie van A op B

waarin $\theta$ de hoek tussen de vectoren is en $|\mathbf {u} |$ en $|\mathbf {v} |$ respectievelijk de normen van de vectoren $\mathbf {u}$ en $\mathbf {v}$ zijn.

Men noteert het inproduct ook als:

\mathbf {u} \cdot \mathbf {v} =(\mathbf {u} ,\mathbf {v} )=\langle \mathbf {u} ,\mathbf {v} \rangle =\langle \mathbf {u} |\mathbf {v} \rangle

Voor de bovenstaande definitie is het nodig de hoek tussen de beide vectoren te kennen, of meer nog dat in de gebruikte meetkunde al een begrip hoek bestaat.

Als de vectoren $\mathbf {u}$ en $\mathbf {v}$ elementen zijn van de $\mathbb {R} ^{n}$ , de $n$ -dimensionale vectorruimte over de reële getallen, en:

\mathbf {u} =(u_{1},u_{2},\ldots ,u_{n})

en

\mathbf {v} =(v_{1},v_{2},\ldots ,v_{n})

dan kan het inwendig product vastgelegd worden als:

\mathbf {u} \cdot \mathbf {v} =u_{1}v_{1}+u_{2}v_{2}+\ldots +u_{n}v_{n}=\sum _{i=1}^{n}u_{i}v_{i}

Deze vorm van het inwendig product heet het standaardinproduct; het is de gebruikelijke vorm van inwendig product in een euclidische ruimte.

Daarna kan dan de hoek tussen de beide vectoren gedefinieerd worden met behulp van dit inproduct en de norm van de vectoren.

Eigenschappen

De vectoren $\mathbf {u}$ en $\mathbf {v}$ staan loodrecht op elkaar, dan en slechts dan als hun inproduct gelijk is aan 0.
Het inwendig product van vectoren uit een reële vectorruimte is commutatief: $\mathbf {u} \cdot \mathbf {v} =\mathbf {v} \cdot \mathbf {u}$

Het begrip inwendig product is ook gegeneraliseerd. Daarbij spreekt men naar analogie van het bovenstaande van "loodrecht" of "orthogonaal" als het inproduct gelijk is aan 0. Het gegeneraliseerde inproduct is echter niet meer noodzakelijk commutatief.

Algemene definitie

Een inwendig product, ook inproduct of scalair product genoemd, op een reële vectorruimte $V$ is een positief definiete symmetrische bilineaire vorm $\langle {\cdot },{\cdot }\rangle \colon V\times V\to \mathbb {R}$ . Dat wil zeggen dat voor $x,y,z\in V$ en $\lambda \in \mathbb {R}$ aan de volgende voorwaarden moet zijn voldaan:

bilineariteit:
- $\langle x+y,z\rangle =\langle x,z\rangle +\langle y,z\rangle$
- $\langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle$
- $\langle x,\lambda y\rangle =\lambda \langle x,y\rangle =\langle \lambda x,y\rangle$
symmetrisch: $\langle x,y\rangle =\langle y,x\rangle$
positief definiet: $\langle x,x\rangle \geq 0$ voor alle $x$ en $\langle x,x\rangle =0\Leftrightarrow x=0$

Een inwendig product of inproduct op een complexe vectorruimte $V$ is een hermitische positief definiete sesquilineaire vorm $\langle {\cdot },{\cdot }\rangle \colon V\times V\to \mathbb {C}$ . Dat wil zeggen dat voor $x,y,z\in V$ en $\lambda \in \mathbb {C}$ aan de volgende voorwaarden moet zijn voldaan:

sesquilineair:
- $\langle x+y,z\rangle =\langle x,z\rangle +\langle y,z\rangle$
- $\langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle$
- $\langle x,\lambda y\rangle =\lambda \langle x,y\rangle =\langle {\bar {\lambda }}x,y\rangle$
hermitisch: $\langle x,y\rangle ={\overline {\langle y,x\rangle }}$
positief definiet: $\langle x,x\rangle >0$ voor $x\neq 0$

Hier is ${\overline {z}}$ de complex geconjugeerde van $z$ .

Een vectorruimte met inwendig product is een inwendig-productruimte.

Eindigdimensionale geval

In $\mathbb {R} ^{n}$ is de algemene vorm van een inwendig product

\langle u,v\rangle =u^{T}Av,

waarin $A$ een positief-definiete matrix is. Omdat iedere positief-definiete matrix geschreven kan worden als $A=B^{T}B$ met $B$ een inverteerbare matrix, en omgekeerd voor een willekeurige inverteerbare matrix $B$ de matrix $A=B^{T}B$ positief definiet is, geldt ook:

\langle u,v\rangle =u^{T}B^{T}Bv=(Bu)^{T}Bv

De matrix $B$ is voor een gegeven $A$ niet uniek bepaald, want de matrix $CB$ met $C$ een orthogonale matrix geeft dezelfde $A$ .

Er geldt dus ook:

\langle u,u\rangle =\|Bu\|_{2}

met de gewone norm.

Voorbeelden

De volgende bewerkingen zijn inwendige producten:

in $\mathbb {R} ^{n}$ :

\langle u,v\rangle =\sum _{k=1}^{n}w_{k}u_{k}v_{k}

waarin

w

een vector van positieve gewichtsfactoren is;

in $\mathbb {C} ^{n}$ :

u\cdot v=u^{T}{\bar {v}}=v^{H}u

waarin

H

staat voor de complex geconjugeerde van de getransponeerde van een vector (de hermitisch toegevoegde);

in een vectorruimte van reëel- of complexwaardige integreerbare functies:

f\cdot g=\int _{a}^{b}{f(t){\overline {g(t)}}\,\mathrm {d} t}

f\cdot g={\frac {1}{b-a}}\int _{a}^{b}{f(t){\overline {g(t)}}\,\mathrm {d} t}

,

waarbij

{\overline {g(t)}}

staat voor de complex geconjugeerde van

g(t)

.

Afhankelijk van de keuze van de vectorruimte van functies, is het positief definiete karakter van dit inproduct niet altijd gegarandeerd; soms moeten equivalentieklassen beschouwd worden van functies die bijna overal aan elkaar gelijk zijn - zie ook Lp-ruimte

van matrices:

A\cdot B=\mathrm {tr} (B^{H}A)

Norm

Bij een inproduct op een willekeurige reële of complexe vectorruimte hoort op natuurlijke wijze een norm

\|x\|={\sqrt {\langle x,x\rangle }}

Een genormeerde vectorruimte waarvan de norm op dergelijke wijze afkomstig is van een inproduct, heet een prehilbertruimte, omdat haar metrische vervollediging een hilbertruimte is.

Het inproduct kan steeds uit de norm worden gereconstrueerd. In een reële prehilbertruimte geldt:

2\langle x,y\rangle =\langle x,y\rangle +\langle y,x\rangle =\|x+y\|^{2}-\|x\|^{2}-\|y\|^{2}

of

2\langle x,y\rangle =\|x\|^{2}+\|y\|^{2}-\|x-y\|^{2}

en ook

4\langle x,y\rangle =\|x+y\|^{2}-\|x-y\|^{2}

In een complexe prehilbertruimte daarentegen geldt:

4\langle x,y\rangle =\|x+y\|^{2}-\|x-y\|^{2}+i\|x+iy\|^{2}-i\|x-iy\|^{2}

Eindigdimensionale geval

In $\mathbb {R} ^{n}$ bepaalt een willekeurig inwendig product een norm met de formule

\|\mathbf {u} \|={\sqrt {\langle \mathbf {u} ,\mathbf {u} \rangle }}=\|B\mathbf {u} \|_{2}

met $B$ een inverteerbare matrix (zie ook boven).

In $\mathbb {R} ^{n}$ zijn er overigens ook nog andere normen, zoals

\|\mathbf {u} \|=\|B\mathbf {u} \|_{p}

voor andere reële waarden van $p\geq 1$ .

Hoek

De ongelijkheid van Cauchy-Schwarz begrenst het inproduct van twee willekeurige vectoren door het product van hun normen:

\forall x,y\in V:|\langle x,y\rangle |\leq \|x\|\cdot \|y\|

De hoek $\alpha$ tussen $x$ en $y$ wordt gegeven door

\cos(\alpha )={\frac {\langle x,y\rangle }{\|x\|\|y\|}}

De ongelijkheid van Cauchy-Schwarz garandeert dat het reële deel van het rechterlid tussen −1 en 1 ligt.

Equivalentie van de beide definities

Afbeelding horend bij bewijs.

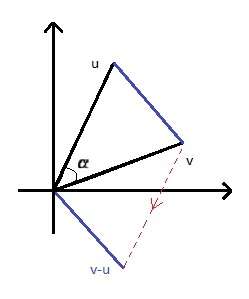
In twee dimensies laat het volgende bewijs zien dat beide definities equivalent zijn. Het bewijs kan heel gemakkelijk doorgetrokken worden naar drie dimensies. Stel gegeven twee vectoren $u=(u_{1},u_{2})$ en $v=(v_{1},v_{2})$ in het vlak. Te bewijzen:

v_{1}u_{1}+v_{2}u_{2}=\|v\|\|u\|\cos(\alpha )

Voor de lengte $L$ van het blauwe lijnstuk in de figuur geldt volgens de stelling van Pythagoras:

L^{2}=(v_{1}-u_{1})^{2}+(v_{2}-u_{2})^{2}

Anderzijds volgt uit de cosinusregel:

L^{2}=\|v\|^{2}+\|u\|^{2}-2\|v\|\|u\|\cos(\alpha )

Gelijkstellen van de beide uitdrukkingen levert:

v_{1}^{2}-2v_{1}u_{1}+u_{1}^{2}+v_{2}^{2}-2v_{2}u_{2}+u_{2}^{2}=v_{1}^{2}+v_{2}^{2}+u_{1}^{2}+u_{2}^{2}-2\|v\|\|u\|\cos(\alpha )

waaruit volgt:

v_{1}u_{1}+v_{2}u_{2}=\|v\|\|u\|\cos(\alpha )

Equivalentie van de beide definities door rotatie ten opzichte van het referentieassenstelsel

Indien we bèta als hoek tussen vector v en de horizontale as in beschouwing nemen en gebruik maken van de Hoeksom- en hoekverschil-identiteiten:

u_{1}=\|u\|\cos(\alpha +\beta )=\|u\|(\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta ))

u_{2}=\|u\|\sin(\alpha +\beta )=\|u\|(\sin(\alpha )\cos(\beta )+\sin(\beta )\cos(\alpha ))

v_{1}=\|v\|\cos(\beta )

v_{2}=\|v\|\sin(\beta )

Waaruit ook volgt dat:

v_{1}u_{1}+v_{2}u_{2}=\|v\|\cos(\beta )\|u\|(\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta ))+\|v\|\sin(\beta )\|u\|(\sin(\alpha )\cos(\beta )+\sin(\beta )\cos(\alpha ))

v_{1}u_{1}+v_{2}u_{2}=\|u\|\|v\|(\cos(\alpha )\cos(\beta )^{2}-\sin(\alpha )\sin(\beta )\cos(\beta )+\sin(\alpha )\sin(\beta )\cos(\beta )+\sin(\beta )^{2}\cos(\alpha ))

v_{1}u_{1}+v_{2}u_{2}=\|u\|\|v\|\cos(\alpha )(\cos(\beta )^{2}+\sin(\beta )^{2})

En bijgevolg equivalent is aan:

v_{1}u_{1}+v_{2}u_{2}=\|u\|\|v\|\cos(\alpha )

Merk ook op dat deze formule aan rechterzijde niet afhankelijk is van de hoek bèta ten opzichte van het orthogonale referentieassenstelsel, noch van de oorsprong van dit assenstelsel en aan linkerzijde wel van de oorsprong van het assenstelsel.

Dus ook al zouden we ons referentieassenstelsel over een willekeurige hoek (bèta) draaien, dan blijft het inwendig product even groot:

v_{1}u_{1}+v_{2}u_{2}=v_{1}'u_{1}'+v_{2}'u_{2}'

'Vrije' vectoren hebben slechts een 'grootte' (En.: 'scalar') en een 'richting' (eventel een 'zin'), en geen bepaald aangrijpingspunt (in tegenstelling tot 'gebonden' vectoren), vandaar dat we ze steeds naar de oorsprong van het orthogonaal assenstelsel kunnen verplaatsen.

Bij een verplaatsing van de oorsprong van het orthogonale assenstelsel zou deze formule immers niet gelden.

Bovendien maakt het niet uit of je de grootte van de ene vector via de hoek alpha projecteert op de andere vector of omgekeerd:

u_{v}=\|u\|\cos(\alpha )

v_{u}=\|v\|\cos(-\alpha )=\|v\|\cos(\alpha )

(Gezien:

\cos(-\alpha )=\cos(\alpha )

)

Om dan vervolgens hun groottes met elkaar te vermenigvuldigen om het inwendig product te bekomen:

\mathbf {u} \cdot \mathbf {v} =\|\mathbf {v} \|u_{v}=\|\mathbf {v} \|\|\mathbf {u} \|\cos(\alpha )=\|\mathbf {u} \|\|\mathbf {v} \|\cos(\alpha )

\mathbf {v} \cdot \mathbf {u} =\|\mathbf {u} \|v_{u}=\|\mathbf {u} \|\|\mathbf {v} \|\cos(-\alpha )=\|\mathbf {u} \|\|\mathbf {v} \|\cos(\alpha )

Wat maakt dat deze bewerking commutatief is in een reële vectorruimte:

\mathbf {u} \cdot \mathbf {v} =\mathbf {v} \cdot \mathbf {u}

Zie ook

Externe links

Minder abstracte uitleg (archief)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.