Euclidische meetkunde

De euclidische meetkunde is een wiskundig systeem dat wordt toegeschreven aan de Griekse wiskundige Euclides van Alexandrië. Zijn werk, de Elementen, is de vroegst bekende systematische bespreking van de meetkunde. De Elementen is een van de meest invloedrijke boeken uit de geschiedenis, niet alleen om de wiskundige inhoud, maar vooral vanwege de gehanteerde methode. Deze methode bestaat eruit om uitgaande van een kleine verzameling van intuïtief aansprekende axioma's, vervolgens vele andere proposities, lemma's en stellingen te bewijzen. Hoewel veel van Euclides' resultaten reeds eerder door vroegere Griekse wiskundigen waren geformuleerd, was Euclides de eerste die liet zien hoe deze proposities in elkaar grijpen in een alomvattend deductief en logisch systeem.

Een weergave van Euclides in een uitvergroting van het schilderij De School van Athene door Raphaël.

De euclidische meetkunde is de meetkunde van ruimte die niet gekromd is. Eerste voorbeeld van een ruimte die wel gekromd is, is het oppervlak van een bol. Belangrijke begrippen in de euclidische meetkunde zijn onder andere de punt, lijn, lijnstuk, kant van de lijn, cirkel met straal en middelpunt, rechte hoek en congruentie. Deze begrippen kennen we, het zijn de begrippen waar het onderwijs in de wiskunde mee begint. We hebben ook een intuïtief beeld van de euclidische meetkunde, maar voor een exacte beschrijving ervan zijn de vijf postulaten van Euclides nodig.

Als eerste axiomatisch systeem begint de Elementen met de meetkunde op een vlak en gebruikt daarbij bovengenoemde begrippen. Hier vindt men ook de eerste voorbeelden van formele bewijzen. De Elementen gaat vervolgens verder met meetkunde van de drie-dimensionale ruimte, de stereometrie. Vooral in de 19e eeuw is de euclidische meetkunde uitgebreid naar elk eindig aantal dimensies. Vooral de leerboeken van de planimetrie en de stereometrie liggen ten grondslag aan de elementaire mechanica en natuurkunde.

Veel van de Elementen bestaat uit resultaten uit wat men tegenwoordig de getaltheorie noemen. Deze resultaten worden in de Elementen echter bewezen met behulp van meetkundige methoden.

Meer dan tweeduizend jaar was het bijvoeglijk naamwoord "euclidisch" overbodig, omdat de euclidische meetkunde de enige bekende vorm van meetkunde was. Euclides' axioma's, met uitzondering van de vijfde, leken zo intuïtief duidelijk dat stellingen, die op basis van deze axioma's werden bewezen door velen in absolute zin als waar beschouwd werden. Vandaag de dag zijn er echter vele andere consistente niet-euclidische meetkundes bekend. De eersten daarvan werden in het begin van de 19e eeuw ontdekt. De niet-euclidische meetkundes hebben vier van de vijf axioma's met de euclidische meetkunde gemeen. Alleen het vijfde, het axioma van de evenwijdige lijnen, volgens welk door een punt P buiten een lijn m slechts één lijn evenwijdig met m loopt, gaat in de niet-euclidische meetkundes niet op. De gewone euclidische meetkunde is te beschouwen als overgangsgeval tussen de elliptische en de hyperbolische meetkunde en wordt om die reden soms ook wel parabolische meetkunde genoemd.

Axiomatische aanpak

De euclidische meetkunde is een axiomatisch systeem, waarin alle stellingen, "ware uitspraken", worden afgeleid uit een eindig aantal axioma's. In het begin van het eerste boek van de Elementen geeft Euclides vijf postulaten, axioma's:

  1. Elk tweetal punten kan worden verbonden door een rechte lijn.
  2. Elk recht lijnstuk kan oneindig worden verlengd tot een rechte lijn.
  3. Gegeven een recht lijnstuk, kan men een cirkel tekenen met dit lijnstuk als straal en een eindpunt van dit lijnstuk als het middelpunt van de cirkel.
  4. Alle rechte hoeken zijn gelijk (in de zin van congruent).
  5. Parallellenpostulaat. Als twee lijnen een derde lijn op zodanige wijze snijden dat de som van de binnenste hoeken aan een kant kleiner is dan twee rechte hoeken, dan moeten deze twee lijnen elkaar onvermijdelijk aan die kant kruisen onder voorwaarde dat deze lijnen oneindig worden verlengd.
Een bewijs uit de Elementen van Euclides dat, gegeven een lijnstuk, er een gelijkzijdige driehoek bestaat waar het gegeven lijnstuk als een van zijdes van de gelijkzijdige driehoek voorkomt. Het bewijs is constructief: een gelijkzijdige driehoek ΑΒΓ wordt gemaakt door cirkels Δ en E te tekenen met respectievelijke middelpunten Α en Β, en door vervolgens een snijpunt van de cirkels als derde hoekpunt van de driehoek te nemen.

Deze axioma's maken gebruik van de volgende concepten: punt, lijn, lijnstuk, kant van de lijn, cirkel met straal en middelpunt, rechte hoek, congruentie, binnenste- en buitenste hoeken, som, eindig en oneindig. De volgende werkwoorden komen voor in de postulaten: verbinden, verlengen, tekenen en kruisen. Van de cirkel die in postulaat 3 wordt beschreven, wordt stilzwijgend aangenomen dat hij uniek is. Postulaat 3 en 5 gaan alleen op voor de vlakke meetkunde; in drie dimensies definieert postulaat 3 een bol. Postulaat 5 leidt tot dezelfde meetkunde als de volgende formulering, die bekendstaat als het axioma van Playfair; ook dit axioma gaat alleen op in het vlak.

"Door een punt, dat niet op een gegeven rechte lijn ligt, kan slechts één en niet meer dan één lijn worden getrokken die de gegeven lijn nooit zal kruisen."

Postulaten 1, 2, 3 en 5 verzekeren het bestaan en de uniciteit van bepaalde meetkundige figuren. Deze verzekeringen zijn van constructieve aard: dat wil zeggen dat ons niet alleen wordt verteld dat bepaalde dingen bestaan, maar dat er ook methoden worden gegeven om deze meetkundige figuren te construeren met een passer en een ongemarkeerde liniaal. In deze zin is de euclidische meetkunde concreter dan vele moderne axiomatische systemen zoals de verzamelingenleer, waar het bestaan van wiskundige objecten vaak wordt verzekerd, zonder uitleg hoe deze objecten kunnen worden geconstrueerd. Soms kunnen de objecten binnen de theorie zelfs niet geconstrueerd worden. Strikt genomen is de constructie van bijvoorbeeld een lijn op papier eerder een wiskundig model van de in het formele systeem gedefinieerde lijn; dit in plaats van een representatie van zo'n lijn. Een euclidische rechte lijn heeft bijvoorbeeld geen breedte en strekt zich naar beide kanten oneindig uit. Elke getekende lijn heeft echter een breedte en is altijd van eindige lengte.

De Elementen gaan uit van vijf "gemeenschappelijke begrippen":

  1. Dingen die gelijk zijn aan hetzelfde ding, zijn gelijk aan elkaar.
  2. Als gelijken worden opgeteld bij gelijken, dan zijn gehelen aan elkaar gelijk.
  3. Als gelijken worden afgetrokken van gelijken, dan zijn resten aan elkaar gelijk.
  4. Dingen die met elkaar samenvallen, zijn aan elkaar gelijk.
  5. Het geheel is groter dan het deel.

Euclides beriep zich ook op andere eigenschappen met betrekking tot groottes.

1 is het enige deel van de onderliggende logica dat expliciet door Euclides is verwoord. 2 en 3 zijn "rekenkundige" beginselen; merk op dat de betekenis van "optellen" en "aftrekken" binnen deze zuiver meetkundige context als gegeven worden beschouwd. 1 tot 4 definiëren in operationele zin het begrip gelijkheid, dat ook kan worden beschouwd als een onderdeel van de onderliggende logica of als een equivalentierelatie, dat, zoals het begrip "samenvallen" een zorgvuldige voorafgaande definitie vereist. 5 is een beginsel van de mereologie. Begrippen als "geheel", "deel" en "rest" vragen om een nauwkeurige definitie. In de 19e eeuw realiseerde men zich dat Euclides' tien axioma's en gemeenschappelijke begrippen niet volstaan om alle bewijzen die in de Elementen voorkomen ook daadwerkelijk te bewijzen. Euclides ging er bijvoorbeeld impliciet van uit dat elke lijn uit ten minste twee punten bestaat. Deze veronderstelling kan niet worden bewezen uit de andere axioma's, en dient daarom als een apart axioma te worden opgenomen.

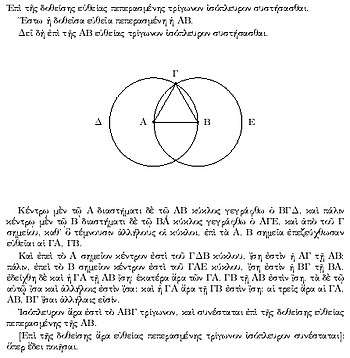
Het allereerste meetkundig bewijs in de Elementen, dat in de figuur rechts van deze tekst wordt getoond, is dat een lijnstuk deel uitmaakt van een gelijkzijdige driehoek; Euclides construeert deze driehoek op de gebruikelijke wijze, door het tekenen van cirkel rondom beide eindpunten (van het lijnstuk) en neemt het snijpunt als het derde hoekpunt. Zijn axioma's garanderen echter niet dat de cirkels elkaar daadwerkelijk snijden, dit omdat zij in overeenstemming zijn met discrete, in plaats van de continue ruimte. Te beginnen met Moritz Pasch in 1882, zijn er veel verbeterde axiomatische systemen voor de meetkunde voorgesteld, waarvan de bekendste de axiomasystemen van David Hilbert, George Birkhoff en Alfred Tarski zijn.

Om eerlijk te zijn ten opzichte van Euclides moet opgemerkt worden dat de eerste formele logica die in staat was zijn meetkunde te ondersteunen die van de Frege uit 1879 was (Begriffsschrift), een tot de jaren vijftig van de twintigste eeuw weinig gelezen werk. Men ziet nu in dat de euclidische meetkunde moet worden ingebed in de eerste-orde logica met identiteit, een formeel systeem dat eerst in 1928 werd opgezet door David Hilbert en Wilhelm Ackermann (Beginselen van de theoretische Logica). De formele mereologie begon pas in 1916, met het werk van Lesniewski en Whitehead. Tarski en zijn studenten hebben tussen 1959 en zijn dood in 1983 belangrijk werk verricht op het gebied van de grondbeginselen van de elementaire meetkunde.

Het parallellenpostulaat

Ook voor de Oud-Griekse wiskundigen leek het parallellenpostulaat al minder vanzelfsprekend dan de andere vier. Experimentele verificatie was uitgesloten alleen al daarom omdat het niet haalbaar is te controleren of twee lijnen zich op een oneindig ver weg gelegen punt al of niet kruisen.[1] Ook Euclides zelf lijkt het vijfde postulaat als kwalitatief verschillend van de anderen te hebben beschouwd, wat blijkt uit de organisatie van de Elementen: de eerste 28 stellingen die hij presenteert, kan hij bewijzen zonder gebruik te maken van het parallellenpostulaat. Door de eeuwen heen hebben veel meetkundigen geprobeerd om het het vijfde postulaat te bewijzen uit de eerste vier postulaten. Zo rond 1763 waren er ten minste 28 verschillende bewijzen gepubliceerd, die alle onjuist bleken.[2] Wij weten nu dat het onmogelijk is om het parallellenpostulaat te bewijzen uitgaande van de andere vier postulaten: dit is in de 19de eeuw aangetoond door de constructie van de alternatieve (niet-euclidische) meetkundige systemen, waar de andere axioma's nog steeds waar zijn, maar waar het parallellenpostulaat wordt vervangen door een daarmee tegenstrijdig axioma. Een onderscheidend aspect van deze systemen is dat de som van de drie hoeken van een driehoek niet gelijk is aan 180°: in de hyperbolische meetkunde is de som van de drie hoeken altijd minder dan 180° en kan deze som zelfs tot nul naderen, terwijl in de elliptische meetkunde de som groter is dan 180°. Als het parallellenpostulaat zonder vervanging uit de lijst van axioma's wordt verwijderd, is het resultaat een meer algemene meetkunde die ook wel absolute meetkunde wordt genoemd.

Analytische meetkunde
Standbeeld van Euclides in het natuurhistorisch museum van de universiteit van Oxford.

De ontwikkeling van de analytische meetkunde verschafte een alternatief om de meetkunde te formaliseren. In deze benadering wordt een punt weergegeven door zijn cartesische x en y coördinaten, wordt een lijn weergeven door haar vergelijking en zo verder. In de 20e eeuw paste dit binnen David Hilberts programma om de gehele wiskunde te reduceren tot rekenkunde om vervolgens de consistentie van de rekenkunde te bewijzen door gebruik te maken van een finitistische redenering. In Euclides' oorspronkelijke benadering volgt de stelling van Pythagoras uit de axioma's van Euclides. In de cartesiaanse benadering gaat men uit van axioma's van de algebra, en is de vergelijking die de stelling van Pythagoras uitdrukt een definitie van een van de termen in de euclidische axioma's, die nu als stellingen worden beschouwd. De vergelijking

die de afstand tussen twee punten en definieert, staat dan bekend als de euclidische metriek. Andere metrieken definiëren niet-euclidische meetkundes.

Zie ook

Voetnoten
  1. Voor de bewering dat dit de historische reden is dat ook de antieken het parallellenpostulaat als minder vanzelfsprekend beschouwden als de andere vier, zie Nagel en Newman 1958, blz. 9.
  2. Hofstadter 1979, blz. 91.

Referenties
  • (en) Boyer, Carl B., A History of Mathematics (Een geschiedenis van de wiskunde), Second Edition. John Wiley & Sons, Inc. (1991). ISBN 0471543977.
  • (en) Heath, Thomas L., The Thirteen Books of Euclid's Elements (De dertien boeken van Euclides' Elementen) (3 vols.), 2nd ed. [Facsimile. Originele publicatie: Cambridge University Press, 1925]. Dover Publications, New York (1956). [[Speciaal:Booksources/0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3)|ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3)]]. Heaths gezaghebbende vertaling van Euclides' Elementen plus zijn uitgebreid historisch onderzoek en uitvoerige commentaren door de gehele tekst.
  • (en) Hofstadter, Douglas R., Gödel, Escher, Bach: An Eternal Golden Braid. Basic Books, New York (1979).
  • (en) Nagel, E. en Newman, J.R., Gödel's Proof (Gödels bewijs), New York University Press, 1958
  • (en) Alfred Tarski, (1951) A Decision Method for Elementary Algebra and Geometry (Een beslissingsmethode voor elementaire algebra en meetkunde). Univ. of California Press.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.