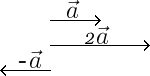Vector (wiskunde)
Een vector (Latijn: drager) is in de wiskunde een element van een vectorruimte, en daarmee een weinig specifiek begrip. Vectorruimten zijn generalisaties van onze gewone driedimensionale ruimte, waarin punten voorgesteld worden door hun drie coördinaten en . Zulke punten, opgevat als pijlen van de oorsprong tot het punt , waren de eerste die vector genoemd werden, een term ingevoerd door William Rowan Hamilton in 1837. Zo'n pijl stelt in de meetkunde en de natuurkunde een grootheid voor die zowel grootte als richting heeft, zoals verplaatsing, snelheid, versnelling, kracht, en dergelijke. Alleen de nulvector heeft geen richting.
Voorstelling van een vector
Om vectoren te onderscheiden van scalaire grootheden, noteert men vectoren meestal als letter met een pijltje erboven, zoals , soms ook als een vetgedrukte letter, bijvoorbeeld . Dit is echter slechts een kwestie van notatie en heeft op zichzelf geen enkele betekenis. In deze notatieconventie wordt de lengte van de vector ( of ) dan aangegeven door een gewone . Men tekent een vector als een pijl, beginnend in z'n aangrijpingspunt.
In de verschillende toepassingen wordt onder meer onderscheid gemaakt tussen vrije vectoren, glijdende vectoren, gebonden vectoren en plaatsvectoren.
Vrije vectoren
Een vrije vector wordt bepaald door een richting en een lengte. Een vrije vector kan overal op het vlak of in de ruimte getekend worden: het blijft dezelfde vector. Omgekeerd: alle vrije vectoren met dezelfde richting en lengte zijn een voorstelling van één en dezelfde vector.
Glijdende vectoren
Een glijdende vector heeft een vaste richting en lengte, maar kan enkel vrij over zijn drager of dragende rechte schuiven of glijden, dus in de richting van de vector en in tegengestelde richting. Een glijdende vector kan overal op de rechte getekend worden: het blijft dezelfde vector. Bijvoorbeeld in het geval van een koppel maakt het glijden van de twee krachten over hun dragers niet uit voor het koppelmoment, terwijl zijdelings verschuiven wel uit zou maken.
Gebonden vector
Een gebonden vector heeft een vast aangrijpingspunt en een vaste richting en lengte. Het aangrijpingspunt is het punt waar vanuit de vector "vertrekt". Iedere functiewaarde van een vectorveld kan worden voorgesteld als een gebonden vector.
Plaatsvector
Een plaatsvector is een gebonden vector met de oorsprong als aangrijpingspunt. Wanneer met plaatsvectoren wordt gerekend, worden de notaties voor een punt en de bijhorende plaatsvector vaak door elkaar gebruikt:
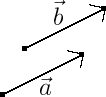
De vector kan worden geschreven als . Als de vector op de tekening een gebonden vector is, is het aangrijpingspunt van . De afbeelding stelt een vector in een tweedimensionale ruimte voor. Men kan ook vectoren in ruimtes met andere dimensies beschouwen. Merk op dat men een vrije vector op verschillende manieren kan tekenen. Wanneer men op eenzelfde afbeelding verschillende malen dezelfde vector tekent, heeft men verschillende, evenwijdige pijltjes van gelijke lengte die in dezelfde richting wijzen. Twee vrije vectoren zijn gelijk als ze dezelfde grootte en richting hebben. Voor gebonden vectoren komt hier nog de eis bij dat ze hetzelfde aangrijpingspunt moeten hebben. Hierdoor ligt de grafische voorstelling van een gebonden vector volledig vast: men kan niet op één afbeelding twee keer (op een verschillende plaats) dezelfde gebonden vector tekenen. De vectoren en op de volgende afbeelding zijn gelijk als het gaat om vrije vectoren, maar verschillend als het gaat om gebonden vectoren, aangezien ze een verschillend aangrijpingspunt hebben.
Vectoren in de gewone driedimensionale ruimte
Een vector in de gewone driedimensionale ruimte (de driedimensionale euclidische ruimte, de klassieke natuurkundige ruimte) kan, na een keuze van een basis, gerepresenteerd worden door componenten. Laat de vectoren , en een basis van de ruimte vormen. Dan kan (per definitie van basis) elke vector geschreven worden als een lineaire combinatie van , en . Dit wil zeggen dat er getallen , en zijn zodat .[1] De vectoren , en heten de componenten van de vector . De getallen , en noemt men de coördinaten of kentallen van ten opzichte van de basis . De volgorde van , en is belangrijk. Indien het duidelijk is over welke basis het gaat, vermeldt men vaak de basis niet.
Twee vectoren zijn gelijk dan en slechts dan als ze dezelfde componenten hebben. Men schrijft wel (met de van hiervoor), als rij:
of als kolom:
Men kan verschillende bewerkingen uitvoeren met vectoren.
In de reële driedimensionale coördinatenruimte is de standaardbasis met de basisvectoren Meetkundig worden ze weergegeven door onderling loodrechte vectoren van eenheidslengte. Men kan hierin lengtes en hoeken definiëren (zie onder) die overeenkomen met de meetkundige begrippen, met als resultaat een driedimensionale euclidische ruimte. Omgekeerd kan men uitgaand van een driedimensionale euclidische ruimte, met gegeven begrippen "lengte" en "loodrecht", drie onderling loodrechte vectoren , en van eenheidslengte als basisvectoren kiezen, zodat een vector beschreven kan worden met zijn drie coördinaten.
In beide gevallen is het resultaat een cartesisch coördinatenstelsel met de basisvectoren waarin een vector wordt geschreven als . In de onderstaande deelparagrafen wordt hiervan gebruikgemaakt.
De richting van noemt men de x-as, van de y-as en van de z-as. Men noemt de standaardbasis ook wel Soms wordt ook de notatie gebruikt: wijst volgens de x-as, volgens de y-as en volgens de z-as; alle drie hebben ze de lengte 1.
Gelijkheid
Van twee vectoren zegt men dat deze gelijk zijn als ze dezelfde grootte en richting hebben.[2]
Equivalent is: van twee vectoren zegt men dat deze gelijk zijn als ze dezelfde coördinaten hebben. Twee vectoren
en
zijn dus gelijk dan en slechts dan als
- .
Optellen van vectoren, parallellogramregel
Het optellen van vectoren kan men doen aan de hand van een tekening in een vlak waar beide inliggen, de zogenoemde parallellogramregel:
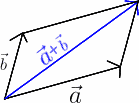
Om te construeren, tekent men en zo, dat de pijltjes die deze vectoren voorstellen in hetzelfde punt vertrekken. Daarna maakt men een parallellogram, zoals op de tekening. Wanneer men dan een pijltje tekent dat begint in hetzelfde punt waar en beginnen, en dat gaat naar de overliggende hoek van het parallellogram, bekomt men een voorstelling van .

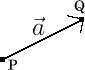
Er bestaat ook een andere manier om te construeren (kop-staartmethode): als het pijltje dat voorstelt, gaat van P naar Q, teken je zo dat het pijltje dat voorstelt, begint in Q. Als dan het pijltje dat voorstelt, stopt in R, is het pijltje van P naar R een voorstelling van de vector . De volgende afbeelding illustreert dit:
Deze tekening illustreert meteen ook de gelijkheid van Chasles-Möbius:
Deze manier is ook toepasbaar bij meerdere vectoren.
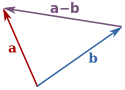
Verschil van vectoren
Het verschil van de vectoren en is gedefinieerd als , waarin de tegengestelde vector van is, dat wil zeggen de vector met dezelfde grootte als , maar met tegengestelde richting (zie het voorbeeld van de scalaire vermenigvuldiging).
Vermenigvuldiging van een vector met een scalair
Scalaire vermenigvuldiging mag niet verward worden met het scalaire product (zie verder).
Om het verschil tussen getallen en vectoren aan te duiden, noemt men een getal ook wel een "scalair": de kentallen van een vector zijn scalairen. Wanneer men een vector vermenigvuldigt met een scalair , krijgt men een nieuwe vector . De grootte van is en de richting is gelijk aan die van als , en wordt omgekeerd als . De volgende afbeelding illustreert de begrippen:
Hierbij is gelijk aan . Als ten opzichte van een bepaalde basis, zal, ten opzichte van diezelfde basis, .
Norm van een vector
De lengte, grootte of norm van de vector wordt aangeduid door of, minder gebruikelijk, met . De norm van een vector dient niet te worden verward met de absolute waarde (een scalaire "norm").
Deze correspondeert met het gewone afstandsbegrip, de euclidische afstand, het afstandsbegrip bepaald door het inproduct van vectoren (zie onder). De norm van de vector kan worden berekend met:
wat een gevolg is van de stelling van Pythagoras aangezien de basisvectoren orthogonale eenheidsvectoren zijn.
Inwendig product
Het inwendig product (ook wel inproduct, scalair product of dot product genoemd) van twee vectoren en zegt iets over de hoek tussen de vectoren. Er geldt namelijk:
- ,
waarin de hoek tussen en is. Soms wordt deze formule als definitie genomen en moet het begrip hoek al bekend zijn. Ook wordt als definitie wel gehanteerd:
- ,
waarin en .
De hoek tussen de vectoren en is dan:
- .
Als minstens een van beide vectoren de nulvector is, is het inwendig product nul en de hoek onbepaald.
Kruisproduct
Voor twee vectoren en in de gewone drie-dimensionale euclidische vectorruimte bestaat ook het kruisproduct (ook wel vectorproduct, uitproduct, uitwendig product of vectorieel product genoemd)
- .
Het kruisproduct is een vector loodrecht op beide vectoren met een grootte gelijk aan de oppervlakte van het parallellogram gevormd door de beide vectoren, en de richting volgens de kurkentrekkerregel (ook rechterhandregel genoemd).
Uitgedrukt in de coördinaten van en luidt het kruisproduct:
- .
Merk op dat het kruisproduct niet commutatief is, maar anticommutatief:
- .
Eenheidsvector

Een eenheidsvector is een vector met een norm gelijk aan 1. Eenheidsvectoren worden vooral gebruikt om een richting aan te geven. Een vector met willekeurige norm ongelijk aan 0 kan worden gedeeld door zijn norm om zo een eenheidsvector te creëren. Dit proces staat bekend als het normaliseren van een vector. Een eenheidsvector wordt wel aangeduid met een dakje, zoals in of ook door .
Om een vector te normaliseren deelt men de vector door zijn lengte :
Nulvector
De nulvector is de vector met lengte nul. In de driedimensionale euclidische ruimte is het de vector met alle coördinaten gelijk aan 0, dus de vector (0,0,0). De nulvector wordt algemeen aangeduid met , met 0, of ook gewoon met 0. In tegenstelling tot enige andere vector, heeft de nulvector geen richting en kan niet worden genormaliseerd (dat wil zeggen dat er geen eenheidsvector is, die een veelvoud is van de nulvector). De som van de nulvector en enige vector is zelf, dat wil zeggen dat .
Vectoren in de natuurkunde
In de natuurkunde wordt onderscheid gemaakt tussen "scalaire grootheden" en "vectoriële grootheden". Het verschil is dat een scalaire grootheid geen richting heeft, en een vectoriële grootheid wel. Voorbeelden van scalaire grootheden uit de natuurkunde zijn: massa, volume, temperatuur, traagheidsmoment, elektrische potentiaal, zwaartekrachtspotentiaal.
Voorbeelden van vectoriële grootheden zijn:
- translatievector, verplaatsingsvector
- snelheid
- versnelling
- kracht
- impuls
- stoot
- impulsmoment
- krachtmoment
In de natuurkunde bestaan ook vectorvelden. Dit zijn velden in de ruimte, waar de grootte en richting van de vector in een punt een functie zijn van de positie . Voorbeelden zijn:
- windveld: dit vectorveld geeft in elke locatie de windrichting en -sterkte aan.
- plaatsvector
- zwaartekrachtveld
- magneetveld
- elektrisch veld
- elektrische stroomdichtheid
Bij de meeste vectoren in de natuurkunde is de grootte (norm, zie boven) geen dimensieloos getal, maar een grootheid uit te drukken als een getal met een eenheid. In het geval van een windveld kan dit bijvoorbeeld 20 km/u zijn.
Vectorruimten in het algemeen
In de context van de lineaire algebra is een vector een element van een vectorruimte.
Boven is het geval van de driedimensionale euclidische ruimte behandeld. De tweedimensionale euclidische ruimte gaat analoog, behalve dat er geen kruisproduct is.
Bij een vectorruimte over een eindig lichaam (Ned) / eindig veld (Be) of over het lichaam (Nederlandse term; in België: veld) van de complexe getallen hebben vectoren geen grootte en richting. Het is ook moeilijk om van deze vectoren een tekening te maken.
Zie ook
Bronnen, noten en/of referenties
|
| Zie de categorie Vector mathematics van Wikimedia Commons voor mediabestanden over dit onderwerp. |