Evenwijdig

Figuur 1. Afstand tussen twee evenwijdige lijnen

Evenwijdige lijnen zijn, in het euclidische vlak (tweedimensionaal), rechte lijnen die geen gemeenschappelijk punt – geen snijpunt – hebben.

Als in het platte vlak twee evenwijdige lijnen worden getekend (zie figuur 1), dan wordt daarmee dat vlak in drie stukken verdeeld: twee stukken die erg veel op elkaar lijken en een strook tussen die lijnen. Als nu op die strook een rechthoek(je) ${\displaystyle PP'Q'Q}$ wordt geplaatst met ${\displaystyle P,\,Q}$ op ${\displaystyle l}$ en ${\displaystyle P',\,Q'}$ op ${\displaystyle m}$, dan past die rechthoek precies tussen de lijnen, en wel op alle plaatsen, mits ${\displaystyle P,\,Q}$ op de lijn ${\displaystyle l}$ en ${\displaystyle P',\,Q'}$ op de lijn ${\displaystyle m}$ blijven liggen. Dat is ook het geval als de lijnen oneindig lang zijn. Daaruit blijkt dat de lijnen onmogelijk een snijpunt kunnen hebben. De breedte van de strook – dat is de lengte van het lijnstukje ${\displaystyle PP'(=QQ')}$ – is de afstand tussen de lijnen ${\displaystyle l,\,m}$.

De breedte van de strook tussen de lijnen ${\displaystyle l}$ en ${\displaystyle m}$ verandert niet, de strook is overal even breed.

Als eerst het rechthoekje wordt neergelegd met een korter lijnstuk ${\displaystyle PP'}$ en vervolgens worden de lijnen getekend, dan wordt de strook natuurlijk steeds smaller. Als bij herhaling daarvan ${\displaystyle P}$ uiteindelijk op ${\displaystyle m}$ komt te liggen, ligt tegelijk ook ${\displaystyle Q}$ op ${\displaystyle m}$.

Voor de ligging van twee lijnen in een plat vlak zijn er dan, zo bekeken, drie mogelijkheden. Ze hebben:

• twee punten gemeenschappelijk – ze vallen samen;
• een punt gemeen – ze snijden elkaar;
• geen punten gemeen – ze zijn evenwijdig.

In de euclidische meetkunde luidt een van de axioma's: door twee verschillende punten gaat precies één rechte lijn. Hebben twee rechte lijnen twee punten gemeen, dan hebben ze dus alle punten gemeen.

Bij meetkundig onderzoek moet redelijk vaak van twee lijnen worden aangetoond dat ze evenwijdig zijn of juist niet. Om zo'n bewijs zo eenvoudig mogelijk te laten verlopen is het handig bij dat bewijs bovenstaande definitie voor evenwijdigheid te gebruiken.

Figuur 2. Kruisende lijnen

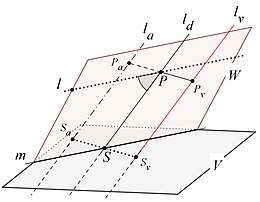
In de euclidische ruimte (driedimensionaal) liggen twee evenwijdige lijnen in eenzelfde vlak. Is dat niet het geval, dan zijn die lijnen kruisend.

Als in de ruimte twee lijnen ${\displaystyle l,\,m}$ in hetzelfde vlak liggen (zie in figuur 2 het vlak ${\displaystyle W}$, dat evenals ${\displaystyle V}$ ook oneindig groot is), dan is de ligging van die lijnen identiek aan de beschreven situatie in de vlakke meetkunde: er is ook zo'n strook in vlak ${\displaystyle W}$, tussen de gestippelde lijn ${\displaystyle l}$ en de lijn ${\displaystyle m}$. Er zijn in dat geval weer drie mogelijkheden: samenvallen (2), snijden (1), evenwijdig (0) – tussen haakjes staat het aantal gemeenschappelijke punten van die lijnen. En dat aantal is gelijk aan het aantal gemeenschappelijke punten van ${\displaystyle l}$ met het vlak ${\displaystyle V}$, immers ${\displaystyle m}$ ligt in ${\displaystyle V}$.

Er is echter nog een mogelijkheid. Met ${\displaystyle P}$ op de lijn ${\displaystyle l}$ wordt ${\displaystyle l}$ vanuit de evenwijdige positie in het vlak ${\displaystyle W}$ gedraaid om ${\displaystyle P}$. Dan ligt het snijpunt ${\displaystyle S}$ van de lijnen in ${\displaystyle V}$ (namelijk steeds op ${\displaystyle m}$). Maar als vervolgens (dus daarna) het punt ${\displaystyle P}$ verplaatst wordt naar een positie voor ${\displaystyle W}$ of achter ${\displaystyle W}$ (${\displaystyle P_{v}}$ en ${\displaystyle P_{a}}$ in de figuur), waarbij de lijn ${\displaystyle l}$ onveranderd in de bereikte positie meegaat (het vlak ${\displaystyle W}$ blijft op z'n plaats), dan snijden ${\displaystyle l_{v}}$ of ${\displaystyle l_{a}}$ de lijn ${\displaystyle m}$ al niet meer bij een kleine verplaatsing van ${\displaystyle P}$, en zo'n verplaatste lijn ligt dan ook niet meer met ${\displaystyle m}$ in eenzelfde vlak. Evenwel, de verplaatste lijn ${\displaystyle l}$ snijdt nog steeds het vlak ${\displaystyle V}$. In deze situatie kruisen de verplaatste lijn ${\displaystyle l}$ en ${\displaystyle m}$ elkaar; zie de punten ${\displaystyle S_{v}}$ en ${\displaystyle S_{a}}$ in het vlak ${\displaystyle V}$.

Per definitie geldt ook:

(a) een lijn is evenwijdig met een vlak als die lijn en dat vlak geen punt gemeen hebben;

(b) twee vlakken zijn evenwijdig als ze geen punt gemeen hebben.

Om min of meer gelijkluidende definities te krijgen bij het snijden van lijnen en vlakken (en ook omdat het handig en verstandig is bij bewijzen) is ook bij ${\displaystyle V//W}$ gekozen voor dan hebben ${\displaystyle V,\,W}$ geen punt gemeen (geen gemeenschappelijke punten). Als ze niet evenwijdig zijn, hebben ze dus 1, 2, 3, ... punten gemeenschappelijk. De wiskunde (stereometrie) maakt het ook in dit geval makkelijk via enkele axioma's namelijk:

(a) als ${\displaystyle V,\,W}$ drie niet op dezelfde lijn gelegen punten gemeen hebben, dan vallen ${\displaystyle V}$ en ${\displaystyle W}$ samen;

Hiermee is ook het aantal van 4, 5, ... niet collineaire gemeenschappelijke punten afgehandeld.

(b) als ${\displaystyle V,\,W}$ twee gemeenschappelijke punten hebben, dan hebben ze de lijn door die twee punten gemeenschappelijk (ze snijden elkaar en de lijn is de snijlijn van beide vlakken);

(c) als ${\displaystyle V,\,W}$ precies één gemeenschappelijk punt hebben, dan hebben ze ook een tweede punt gemeenschappelijk (en zie dan weer geval b; ze snijden elkaar).

${\displaystyle l//m}$ betekent: de lijnen ${\displaystyle l,m}$ zijn evenwijdig of: de lijn ${\displaystyle l}$ is evenwijdig met de lijn ${\displaystyle m}$. Het teken ${\displaystyle //}$ heeft dezelfde betekenis bij lijn ${\displaystyle //}$ vlak en vlak ${\displaystyle //}$ vlak.

Tweedimensionaal

• twee lijnen die loodrecht staan op dezelfde rechte lijn, zijn evenwijdig (stelling);
• de lijn door de middens van twee zijden van een driehoek is evenwijdig met de (drager van de)[1] derde zijde van die driehoek (stelling);
• de (dragers van de) zijden van een parallellogram zijn twee aan twee evenwijdig (definitie); en daarmee ook, twee aan twee, de zijden van een rechthoek en een vierkant;
• een regelmatige zeshoek heeft drie paar evenwijdige zijden (stelling);
• (buiten de wiskunde) de notenbalk op muziekpapier.

Driedimensionaal

• twee lijnen die loodrecht staan op hetzelfde vlak, zijn evenwijdig (stelling);
• de (dragers van de) ribben van een prisma zijn evenwijdig (definitie) en daarmee ook de ribben van de lichamen blok en balk;
• de beschrijvenden van een cilindervlak zijn evenwijdig (definitie);
• bij een rechte cirkelcilinder zijn de doorsneden van het cilindervlak met een vlak loodrecht op de as evenwijdige cirkels (stelling);
• de zijvlakken van een kubus zijn twee aan twee evenwijdig.
• (buiten de wiskunde): buiten- en binnenmuur van een gebouw, glasplaten bij dubbelglas; schappen in een boekenkast.

Figuur 4. Lengte van het loodrechte verbindingslijnstuk

Figuur 5. Lijn evenwijdig met een vlak

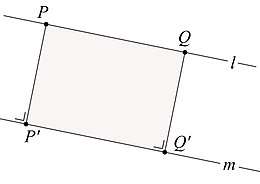
• De lengte van het loodrechte verbindingslijnstuk van een punt van lijn met een punt van een daarmee evenwijdige lijn is voor alle punten van die lijn gelijk (informeel: twee evenwijdige lijnen hebben overal dezelfde afstand).

In figuur 4 zijn de lijnen ${\displaystyle l,\,m}$ evenwijdig. ${\displaystyle P}$ is een punt van ${\displaystyle l}$ en ${\displaystyle Q}$ is een willekeurig ander punt van ${\displaystyle l}$; ${\displaystyle P',\,Q'}$ zijn de loodrechte projecties van ${\displaystyle P,\,Q}$ op ${\displaystyle m}$. ${\displaystyle PP',\,QQ'}$ zijn de onderlinge loodrechte verbindingslijnstukken. Nu is vierhoek ${\displaystyle PP'Q'Q}$ een rechthoek, zodat ${\displaystyle PP'=QQ'}$. Hetgeen moest worden aangetoond.

Deze eigenschap biedt de mogelijkheid om ook samenvallende lijnen evenwijdig te noemen, hun afstand is overal gelijk aan nul.

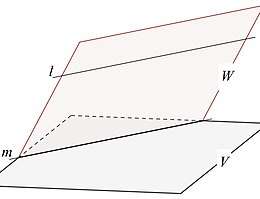
• Een lijn ${\displaystyle l}$ die evenwijdig is met een vlak ${\displaystyle V}$, is evenwijdig met een lijn ${\displaystyle m}$ in ${\displaystyle V}$.

In figuur 5 is ${\displaystyle W}$ een vlak door ${\displaystyle l}$ dat ${\displaystyle V}$ snijdt. De snijlijn van ${\displaystyle V}$ en ${\displaystyle W}$ is ${\displaystyle m}$. Omdat ${\displaystyle l//V}$ is, heeft ${\displaystyle l}$ geen punt gemeen met ${\displaystyle V}$. ${\displaystyle l}$ heeft dus ook geen punt gemeen met ${\displaystyle m}$ (hier wordt dus de definitie gebruikt), maar ${\displaystyle l}$ ligt wel met ${\displaystyle m}$ in hetzelfde vlak ${\displaystyle W}$. Dus ${\displaystyle l//m}$.

Hebben de evenwijdige lijnen ${\displaystyle l,\,m}$ in een standaard ${\displaystyle xOy}$-assenstelsel de vergelijkingen

${\displaystyle l:\ \ y=rx+a\ \ \ \ \ \ m:\ \ y=rx+b}$

dan kan de lengte ${\displaystyle d}$ (${\displaystyle ={\text{afstand}}(l,\,m)}$) van een loodrecht verbindingslijnstuk, worden berekend. De coördinaten van de eindpunten ${\displaystyle P,\,P'}$ van zo'n lijnstuk zijn de oplossingen van de stelsels vergelijkingen:

${\displaystyle \left\{{\begin{array}{*{35}{l}}y=rx+a\\y=-{\tfrac {1}{r}}x\\\end{array}}\right.\ \ \ \ \ \ \left\{{\begin{array}{*{35}{l}}y=rx+b\\y=-{\tfrac {1}{r}}x\\\end{array}}\right.}$

De tweede vergelijking van elk stelsel is de vergelijking van de door het punt ${\displaystyle O}$ gaande drager van het loodlijnstuk.

De oplossingen zijn:

${\displaystyle P=\left({\frac {-ra}{r^{2}+1}},{\frac {a}{r^{2}+1}}\right)\ \ \ \ \ \ P'=\left({\frac {-rb}{r^{2}+1}},{\frac {b}{r^{2}+1}}\right)}$

Bijgevolg:

${\displaystyle d={\frac {|a-b|}{\sqrt {r^{2}+1}}}}$

In de vergelijkingen van de lijnen ${\displaystyle l,\,m}$ hierboven is het getal ${\displaystyle r}$ – de vermenigvuldigingsfactor van ${\displaystyle x}$ – de richtingscoëfficiënt: ${\displaystyle r}$ bepaalt de richting van de lijnen. De lijnen hebben dus dezelfde richting, of anders gezegd: ${\displaystyle l//m}$. Als ${\displaystyle a=b}$ is, vallen de lijnen samen, immers uit de formule voor ${\displaystyle d}$ volgt dan ${\displaystyle d=0}$. Hiermee wordt duidelijk dat samenvallende rechte lijnen kunnen worden beschouwd als zijnde evenwijdig.

• Evenwijdigheid als hierboven bedoeld, is afhankelijk van het zogenoemde parallellenpostulaat van Euclides, het 5e axioma in diens Elementen. Dit axioma luidt, in de vorm zoals het geïntroduceerd is door John Playfair (1748-1819):
  • Door een punt gelegen buiten een rechte lijn gaat precies één rechte lijn die met die rechte lijn evenwijdig is.

• Evenwijdigheid is alleen een zinvol begrip in de euclidische meetkunde. In niet-euclidische meetkundes gelden ingewikkelder afspraken met betrekking tot de snijpunten van twee lijnen.

• Bij bepaalde meetkundige (ook euclidische) configuraties is het soms handig af te spreken dat twee evenwijdige lijnen elkaar in het oneindige snijden, een oneigenlijk snijpunt hebben. Dit is gebaseerd op het verschijnsel dat de hoek tussen twee elkaar snijdende lijnen steeds kleiner wordt naarmate die lijnen de evenwijdige positie naderen. Daarbij komt het hoekpunt steeds verder weg te liggen. Via de limiet, bij evenwijdigheid, komt het punt dan in het oneindige te liggen.

• In het lijnperspectief lijken evenwijdige lijnen elkaar ook te snijden in het verdwijnpunt.

Figuur 7. Huygenscirkels

Figuur 8. Twee parallelkrommen van ${\displaystyle K:\,y=3\sin({\tfrac {1}{2}}x)}$

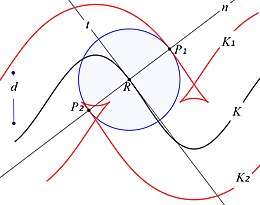
Ook bij krommen (kromme lijnen) kan evenwijdigheid aan de orde komen. Daarbij is evenwel het ontbreken van snijpunten niet voldoende (een parabool en een geheel daarbinnen gelegen cirkel zullen zeker niet evenwijdig genoemd worden). Daarom is het gebruikelijk ook de afstand ${\displaystyle d}$ van een punt ${\displaystyle P}$ tot een kromme ${\displaystyle K}$ erbij te betrekken; in formule:[2]

${\displaystyle d={\text{afstand}}(P,K)={\text{minimum}}\{\left|XP\right|\ {\text{waarbij}}\ \forall X:X\in K\}}$

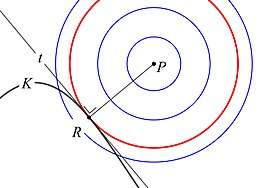
Het vinden van de waarde van ${\displaystyle d}$ is in de praktijk soms een probleem. Er kan evenwel gebruik gemaakt worden van huygenscirkels,[3] dit zijn concentrische cirkels met ${\displaystyle P}$ als middelpunt. ${\displaystyle d}$ is dan de lengte van de straal van de kleinste huygenscirkel die precies één punt ${\displaystyle R\,(=X)}$ met ${\displaystyle K}$ gemeen heeft; zie figuur 7.

In het algemeen zal ${\displaystyle R}$ het gemeenschappelijk raakpunt zijn van die huygenscirkel en ${\displaystyle K}$. Het lijnstuk ${\displaystyle RP}$ staat dan in ${\displaystyle R}$ loodrecht op de raaklijn ${\displaystyle t}$ in ${\displaystyle R}$ aan de cirkel.

Daarbij past de volgende (wat informele) definitie, die ook te gebruiken is bij de constructie van ${\displaystyle K'}$:

• De krommen ${\displaystyle K}$ en ${\displaystyle K'}$ zijn evenwijdig indien de punten ${\displaystyle P}$ van ${\displaystyle K'}$ verkregen kunnen worden door op de normaal ${\displaystyle n}$[4] van ${\displaystyle K}$ in de punten ${\displaystyle R}$ van ${\displaystyle K}$ een lijnstuk ${\displaystyle RP}$ met ${\displaystyle |RP|=d}$ steeds aan dezelfde kant van ${\displaystyle K}$ af te zetten. ${\displaystyle K}$ en ${\displaystyle K'}$ zijn in dit geval parallelkrommen.

Het resultaat van een bewerking op een kromme ${\displaystyle K}$ volgens deze definitie is een kromme ${\displaystyle K'}$ die in het algemeen niet van hetzelfde type is als ${\displaystyle K}$ (${\displaystyle K'}$ is van een hogere graad dan ${\displaystyle K}$). Alleen de rechte lijn en de cirkel geven parallelkrommen die gelijkvormig zijn met het origineel. Zelfs bij kleine waarden van ${\displaystyle d}$ kunnen gladde krommen een parallelkromme hebben met singulariteiten (zie figuur 8).

De kromme ${\displaystyle K'}$ wordt ook wel de iso-afstandslijn van ${\displaystyle K}$ genoemd; zie Externe Link, Math4all.

Als de kromme ${\displaystyle K}$ in ${\displaystyle \mathbb {R} ^{2}}$ is vastgelegd met de vectorvergelijking

${\displaystyle {\vec {x}}(t)=(\,x(t),\,y(t)\,)}$

dan is de kromme ${\displaystyle K'}$ een parallelkromme van ${\displaystyle K}$ als ${\displaystyle K'}$ de volgende vectorvergelijking heeft:

${\displaystyle {{\vec {x}}_{d}}(t)={\vec {x}}(t)+d\cdot {\vec {n}}(t)}$

Daarin is ${\displaystyle d\neq 0}$ en ${\displaystyle {\vec {n}}}$ de normaalvector van ${\displaystyle {\vec {x}}}$ met lengte ${\displaystyle 1}$.

Als een van de weinige talen heeft het Nederlands voor het bedoelde begrip met evenwijdig een eigen term. De term is bedacht door Simon Stevin (1548-1620). Andere talen hebben meestal een woord dat overeenkomt met of is afgeleid van parallel (< Gr. παράλληλος (par-allè-los), dat naast elkaar betekent). Uit zuiver wiskundig oogpunt is de term parallel te verkiezen, omdat evenwijdig (even wijd van elkaar) een eigenschap van parallelle lijnen uitdrukt die niet in de definitie vermeld wordt,[5] het is een bewijsbare eigenschap van die lijnen.

In de aardrijkskunde worden de denkbeeldige breedtecirkels op de aarde ook parallelcirkels of parallellen genoemd. Elke breedtecirkel is dan evenwijdig met de evenaar, een van de wiskunde afwijkend afstandsbegrip.

Het woord parallel wordt ook in de elektrotechniek en elektronica gebruikt. Bij een parallelschakeling van twee of meer componenten zijn die zo in een schakeling aangebracht dat de spanning op alle componenten gelijk is. Parallelgeschakelde componenten hoeven in een schakeling niet evenwijdig geplaatst te zijn, als maar aan de bovenstaande voorwaarde wordt voldaan.

Figuur 9. (a) Offset-curve en (b) iso-afstandslijn van een vierkant

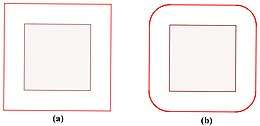
In CAD-programma's kunnen concentrische cirkels, evenwijdige lijnen, bogen en oppervlakken worden getekend met speciale opdrachten.[6] Alleen rechte lijnen en cirkels geven figuren die voldoen aan de genoemde definitie van evenwijdig, zie figuur 9.

In de taalkunde is parallellisme een stijlfiguur.

In de psychotherapie is een parallelproces een interactiepatroon tussen groepen van mensen.[7]

In het dagelijks taalgebruik komt het woord parallel ook voor in andere betekenissen dan evenwijdig. Zoals:

• gelijkend op: parallellen trekken is het benoemen van gelijkenissen of verwantschappen tussen twee dingen;
• gelijktijdig: parallelprocessor, parallelmarkt, parallelklas of -groep;
• er naast gelegen of er naast: parallelweg, parallelrijbaan, parallelrijstrook, parallelimport.

• Antiparallel
• F- en Z-hoeken
• Loodrecht (meetkunde)
• Conflictlijn
• Territoriale wateren

• Math4all: Iso afstandslijnen (afstanden en grenzen)
• Eric W. Weisstein: (en) Parallel Curves. Via: MathWorld--A Wolfram Web Resource