Householder-transformatie

Householder-transformatie in het vlak: de vector ${\displaystyle x}$ wordt getransformeerd naar ${\displaystyle Hx}$ door spiegeling aan het hypervlak (hier een lijn) dat de hoek tussen ${\displaystyle x}$ en ${\displaystyle Hx}$ in tweeën deelt

Een van de technieken om de QR-decompositie van een matrix te berekenen gebruikt Householder-transformaties om nullen te verkrijgen in de benedendriehoek van de matrix (analoog aan wat bij Gauss-eliminatie gebeurt).

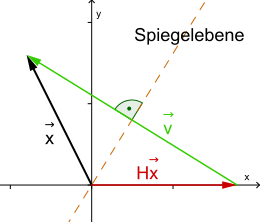
Om de vector ${\displaystyle x}$ met een spiegeling ${\displaystyle H}$ zo te spiegelen dat de gespiegelde ${\displaystyle Hx}$op de x-as ligt, moet gespiegeld worden aan een hypervlak dat de hoek tussen ${\displaystyle x}$ en ${\displaystyle e_{1}=(1,0,\ldots ,0)}$ in twee gelijke delen verdeelt. De genormeerde normaalvector van dat hypervlak is:

${\displaystyle u={\frac {x-\|x\|e_{1}}{\|x-\|x\|e_{1}\|}}}$.

De gespiegelde vector is dan

${\displaystyle Hx=(\|x\|,0,\ldots ,0)}$.

Het beeld onder een Householder-transformatie van een vector kan men snel berekenen: men moet ${\displaystyle 2uu^{T}x}$ aftrekken van ${\displaystyle x}$. Dit vereist de berekening van een inwendig product en het verschil van een vector met een veelvoud van een andere vector.

In de QR-decompositie wordt een matrix ${\displaystyle A}$ herleid tot een bovendriehoeksmatrix ${\displaystyle R}$ door opeenvolgende Householder-transformaties ${\displaystyle H_{1},H_{2},...H_{p}}$, met normaalvectoren ${\displaystyle u_{1},u_{2},...}$ die orthogonaal zijn ten opzichte van elkaar, zodanig dat in de kolommen van ${\displaystyle A}$ de elementen onder de diagonaal nul worden. Dan is

${\displaystyle R=H_{p}\cdots H_{2}H_{1}A}$

De orthogonale matrix ${\displaystyle Q}$ wordt bepaald door ${\displaystyle R=Q^{T}A}$; dat wil zeggen:

${\displaystyle Q^{T}=H_{p}\cdots H_{1}}$

De QR-decompositie kan men ook langs andere wegen bekomen, bijvoorbeeld via Givens-rotaties.