Erlang distribution

Erlang
	Probability density function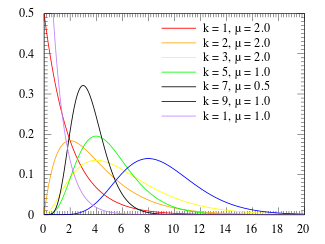
	Cumulative distribution function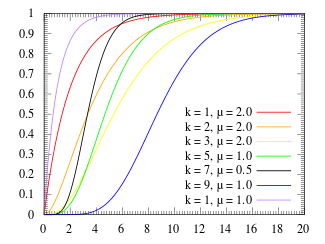
Parameters	shape ; rate ; alt.: scale
Support
PDF
CDF
Mean
Median	No simple closed form
Mode
Variance
Skewness
Ex. kurtosis
Entropy
MGF	for
CF

The Erlang distribution is a two-parameter family of continuous probability distributions with support $x\in [0,\infty )$ . The two parameters are:

a positive integer $k,$ the "shape", and
a positive real number $\lambda ,$ the "rate". The "scale", $\mu ,$ the reciprocal of the rate, is sometimes used instead.

The Erlang distribution with shape parameter $k=1$ simplifies to the exponential distribution. It is a special case of the gamma distribution. It is the distribution of a sum of $k$ independent exponential variables with mean $1/\lambda$ each.

The Erlang distribution was developed by A. K. Erlang to examine the number of telephone calls which might be made at the same time to the operators of the switching stations. This work on telephone traffic engineering has been expanded to consider waiting times in queueing systems in general. The distribution is now used in the fields of stochastic processes and of biomathematics.

Characterization

Probability density function

The probability density function of the Erlang distribution is

f(x;k,\lambda )={\lambda ^{k}x^{{k-1}}e^{{-\lambda x}} \over (k-1)!}\quad {\mbox{for }}x,\lambda \geq 0,

The parameter k is called the shape parameter, and the parameter $\lambda$ is called the rate parameter.

An alternative, but equivalent, parametrization uses the scale parameter $\mu$ , which is the reciprocal of the rate parameter (i.e., $\mu =1/\lambda$ ):

f(x;k,\mu )={\frac {x^{{k-1}}e^{{-{\frac {x}{\mu }}}}}{\mu ^{k}(k-1)!}}\quad {\mbox{for }}x,\mu \geq 0.

When the scale parameter $\mu$ equals 2, the distribution simplifies to the chi-squared distribution with 2k degrees of freedom. It can therefore be regarded as a generalized chi-squared distribution for even numbers of degrees of freedom.

Because of the factorial function in the denominator, the Erlang distribution is only defined when the parameter k is a positive integer. In fact, this distribution is sometimes called the Erlang-k distribution (e.g., an Erlang-2 distribution is an Erlang distribution with $k=2$ ). The gamma distribution generalizes the Erlang distribution by allowing k to be any positive real number, using the gamma function instead of the factorial function.

Cumulative distribution function (CDF)

The cumulative distribution function of the Erlang distribution is

F(x;k,\lambda )={\frac {\gamma (k,\lambda x)}{(k-1)!}},

where $\gamma$ is the lower incomplete gamma function. The CDF may also be expressed as

F(x;k,\lambda )=1-\sum _{{n=0}}^{{k-1}}{\frac {1}{n!}}e^{{-\lambda x}}(\lambda x)^{n}.

Median

An asymptotic expansion is known for the median of an Erlang distribution,^[1] for which coefficients can be computed and bounds are known.^[2]^[3] An approximation is ${\frac {k}{\lambda }}\left(1-{\dfrac {1}{3k+0.2}}\right),$ i.e. below the mean ${\frac {k}{\lambda }}.$ ^[4]

Generating Erlang-distributed random variates

Erlang-distributed random variates can be generated from uniformly distributed random numbers ( $U\in (0,1]$ ) using the following formula:^[5]

E(k,\lambda )\approx -{\frac {1}\lambda }\ln \prod _{{i=1}}^{k}U_{{i}}

Occurrence

Waiting times

Events that occur independently with some average rate are modeled with a Poisson process. The waiting times between k occurrences of the event are Erlang distributed. (The related question of the number of events in a given amount of time is described by the Poisson distribution.)

The Erlang distribution, which measures the time between incoming calls, can be used in conjunction with the expected duration of incoming calls to produce information about the traffic load measured in erlangs. This can be used to determine the probability of packet loss or delay, according to various assumptions made about whether blocked calls are aborted (Erlang B formula) or queued until served (Erlang C formula). The Erlang-B and C formulae are still in everyday use for traffic modeling for applications such as the design of call centers.

It has also been used in business economics for describing interpurchase times.^[6]

Stochastic processes

The Erlang distribution is the distribution of the sum of k independent and identically distributed random variables each having an exponential distribution. The long-run rate at which events occur is the reciprocal of the expectation of $X$ , that is $\lambda /k$ . The (age specific event) rate of the Erlang distribution is, for $k>1$ , monotonic in $x$ , increasing from zero at $x=0$ , to $\lambda$ as $x$ tends to infinity.^[7]

Related distributions

If $X\sim \operatorname {Erlang} (k,\lambda )$ then $a\cdot X\sim \operatorname {Erlang} \left(k,{\frac {\lambda }{a}}\right)$ with $a\in {\mathbb {R}}$
If $X\sim \operatorname {Erlang} (k_{1},\lambda )$ and $Y\sim \operatorname {Erlang} (k_{2},\lambda )$ then $X+Y\sim \operatorname {Erlang} (k_{1}+k_{2},\lambda )$
If $X_{i}\sim \operatorname {Exponential} (\lambda ),$ then $\sum _{i=1}^{k}{X_{i}}\sim \operatorname {Erlang} (k,\lambda )$
If k is an integer and $X\sim \operatorname {Gamma} (k,\lambda ),$ then $X\sim \operatorname {Erlang} (k,\lambda )$
If $U\sim \operatorname {Exponential} (\lambda )$ and $V\sim \operatorname {Erlang} (n,\lambda )$ then ${\frac {U}{V}}+1\sim \operatorname {Pareto} (1,n)$
The Erlang distribution is a special case of the Pearson type III distribution
The chi-squared distribution is a special case of the Erlang distribution. Indeed, if $X\sim \operatorname {Erlang} (k,\lambda )$ , then $2\lambda X\sim \chi _{2k}^{2}$ .
The Erlang distribution is related to the Poisson distribution by the Poisson process: If $S_{n}=\sum _{i=1}^{n}X_{i}$ such that $X_{i}\sim \operatorname {Exponential} (\lambda ),$ then $S_{n}\sim \operatorname {Erlang} (n,\lambda )$ and $\operatorname {Pr} (N(x)\leq n)=\operatorname {Pr} (S_{n}\geq x)=1-F_{X}(x;n,\lambda )=\sum _{k=0}^{n-1}{\frac {1}{k!}}e^{-\lambda x}(\lambda x)^{k}.$ Taking the differences over $n$ gives the Poisson distribution.

Notes

↑ Choi, K. P. (1994). "On the medians of gamma distributions and an equation of Ramanujan". Proceedings of the American Mathematical Society. 121: 245–251. doi:10.1090/S0002-9939-1994-1195477-8. JSTOR 2160389.
↑ Adell, J. A.; Jodrá, P. (2007). "On a Ramanujan equation connected with the median of the gamma distribution". Transactions of the American Mathematical Society. 360 (7): 3631. doi:10.1090/S0002-9947-07-04411-X.
↑ Jodrá, P. (2012). "Computing the Asymptotic Expansion of the Median of the Erlang Distribution". Mathematical Modelling and Analysis. 17 (2): 281–292. doi:10.3846/13926292.2012.664571.
↑ Banneheka BMSG, Ekanayake GEMUPD (2009) "A new point estimator for the median of gamma distribution". Viyodaya J Science, 14:95-103
↑ Resa. "Statistical Distributions - Erlang Distribution - Random Number Generator". www.xycoon.com. Retrieved 4 April 2018.
↑ C. Chatfield and G.J. Goodhardt: “A Consumer Purchasing Model with Erlang Interpurchase Times”; Journal of the American Statistical Association, Dec. 1973, Vol.68, pp.828-835
↑ Cox, D.R. (1967) Renewal Theory, p20, Methuen.

References

Ian Angus "An Introduction to Erlang B and Erlang C", Telemanagement #187 (PDF Document - Has terms and formulae plus short biography)

External links

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Choi, K. P. (1994). "On the medians of gamma distributions and an equation of Ramanujan". Proceedings of the American Mathematical Society. 121: 245–251. doi:10.1090/S0002-9939-1994-1195477-8. JSTOR 2160389.

[2] Adell, J. A.; Jodrá, P. (2007). "On a Ramanujan equation connected with the median of the gamma distribution". Transactions of the American Mathematical Society. 360 (7): 3631. doi:10.1090/S0002-9947-07-04411-X.

[3] Jodrá, P. (2012). "Computing the Asymptotic Expansion of the Median of the Erlang Distribution". Mathematical Modelling and Analysis. 17 (2): 281–292. doi:10.3846/13926292.2012.664571.

[Banneheka2009-4] Banneheka BMSG, Ekanayake GEMUPD (2009) "A new point estimator for the median of gamma distribution". Viyodaya J Science, 14:95-103

[5] Resa. "Statistical Distributions - Erlang Distribution - Random Number Generator". www.xycoon.com. Retrieved 4 April 2018.

[6] C. Chatfield and G.J. Goodhardt: “A Consumer Purchasing Model with Erlang Interpurchase Times”; Journal of the American Statistical Association, Dec. 1973, Vol.68, pp.828-835

[7] Cox, D.R. (1967) Renewal Theory, p20, Methuen.

Probability distributions
List
Discrete univariate with finite support	Benford Bernoulli beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot
Discrete univariate with infinite support	beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta
Continuous univariate supported on a bounded interval	arcsine ARGUS Balding–Nichols Bates beta beta rectangular Irwin–Hall Kumaraswamy logit-normal noncentral beta raised cosine reciprocal triangular U-quadratic uniform Wigner semicircle
Continuous univariate supported on a semi-infinite interval	Benini Benktander 1st kind Benktander 2nd kind beta prime Burr chi-squared chi Dagum Davis exponential-logarithmic Erlang exponential F folded normal Flory–Schulz Fréchet gamma gamma/Gompertz generalized inverse Gaussian Gompertz half-logistic half-normal Hotelling's T-squared hyper-Erlang hyperexponential hypoexponential inverse chi-squared scaled inverse chi-squared inverse Gaussian inverse gamma Kolmogorov Lévy log-Cauchy log-Laplace log-logistic log-normal Lomax matrix-exponential Maxwell–Boltzmann Maxwell–Jüttner Mittag-Leffler Nakagami noncentral chi-squared Pareto phase-type poly-Weibull Rayleigh relativistic Breit–Wigner Rice shifted Gompertz truncated normal type-2 Gumbel Weibull Discrete Weibull Wilks's lambda
Continuous univariate supported on the whole real line	Cauchy exponential power Fisher's z Gaussian q generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson's S_U Landau Laplace asymmetric Laplace logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel Tracy–Widom variance-gamma Voigt
Continuous univariate with support whose type varies	generalized extreme value generalized Pareto Marchenko–Pastur q-exponential q-Gaussian q-Weibull shifted log-logistic Tukey lambda
Mixed continuous-discrete univariate	rectified Gaussian
Multivariate (joint)	Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet generalized Dirichlet multivariate Laplace multivariate normal multivariate stable multivariate t normal-inverse-gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart
Directional	Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped asymmetric Laplace wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham
Degenerate and singular	Degenerate Dirac delta function Singular Cantor
Families	Circular compound Poisson elliptical exponential natural exponential location–scale maximum entropy mixture Pearson Tweedie wrapped