Bewerkingsvolgorde
Bewerkingsvolgorde slaat op het stelsel van gewoonteregels met betrekking tot de interpretatie van wiskundige of logische expressies met meerdere bewerkingen, voor wat betreft de volgorde van uitvoering van de bewerkingen (de sterkte van de binding). Ook programmeertalen hebben zulke regels.
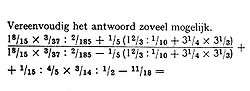
Voor het afwijken van de standaardvolgorde, en soms ook wel ten overvloede, voor de duidelijkheid, worden haakjes gebruikt.
Rekenen
Moderne volgorde
De moderne volgorde, die in de Nederlandse wiskundeschoolboeken beschreven en geoefend wordt, is:
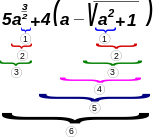
- haakjes; met het voorop staan van haakjes wordt bedoeld dat bijvoorbeeld met binaire operaties en en operanden en , niet eerst wordt bepaald - dwars door het haakje heen, maar met .
- machtsverheffen en worteltrekken
- vermenigvuldigen en delen
- optellen en aftrekken
Bewerkingen die in de lijst op gelijke hoogte staan, zoals optellen en aftrekken, zijn gelijkwaardig. Gelijkwaardige bewerkingen worden van links naar rechts uitgevoerd, behalve dat betekent [1], en dat voor de lineaire notatie a^b^c beide interpretaties voorkomen.
Een ezelsbruggetje voor deze volgorde exclusief aanwijzingen voor gelijkwaardigheid, is: Hoe moeten wij van de onvoldoendes afkomen?. En een ezelsbruggetje inclusief aanwijzingen voor de gelijkwaardigheid is: Hé, Mw. v/d Aorta!.
Oudere volgorde
De plaats van de w in het oude, achterhaalde ezelsbruggetje Meneer van Dalen wacht op antwoord laat zien dat enkele toonaangevende 19e-eeuwse leerboeken een andere opvatting verkondigden over de gangbare volgorde. Het eerste bekende Nederlandse leerboek dat die volgorde expliciet beschreef, en samenvatte in een ranglijst, was Beginselen der stelkunst, voor de kadetten van alle wapenen van Badon Ghijben en Strootman, van de Koninklijke Militaire Academie (1838)[2]:
- De schrijvers lieten de haakjes, die ze wel degelijk gebruikten, buiten de lijst omdat haakjes geen bewerking zijn.
- Delen was dus ondergeschikt aan vermenigvuldigen. 12 : 4 × 3 was 1, terwijl dat nu 9 is.
- Worteltrekken stond opmerkelijk laag. √ 4 × 3 was √(12), terwijl het nu 6 is.
Een bekend leerboek voor het lager onderwijs dat deze ranglijst geheel overnam was het Leerboek der Rekenkunde van Jan Versluys uit 1875.[3] Dat Versluys de ranglijst van Badon Ghijben overnam betekent niet dat er in het 19e-eeuwse onderwijs overeenstemming bestond over die volgorde; met name over de betekenis van waren de meningen verdeeld.[4] Beide leerboeken behandelden de ranglijst ook niet als leerstof maar als bijzaak, in een appendix, zonder oefensommetjes. Later werden lastige onderbehaakte oefensommetjes op scholen soms een doel op zich, en werd het ezelsbruggetje Meneer van Dalen wacht op antwoord bedacht. In de tweede helft van de 20e eeuw kozen veel schoolboeken voor de moderne bewerkingsvolgorde die internationaal regel was, mede door de invloed van de programmeertalen van de jaren 60-70 (Fortran, Algol, Pascal en C). Het oude ezelsbruggetje werd afgezworen, hoewel het nog enigszins bruikbaar zou blijven: de veranderde plaats van worteltrekken maakte in de praktijk weinig uit omdat de wortels in bijna alle boeken voorzien werden van een bovenstreep of haakjes.[5] De veranderde gelijkwaardigheid van vermenigvuldigen en delen maakte niet uit voor het ezelsbruggetje omdat dit van oudsher geen aanwijzingen voor gelijkwaardigheid bevatte, ook niet voor de oude gelijkwaardigheid van optellen en aftrekken.
Een enkele wiskundeschoolboekenserie handhaafde bovenstreeploze wortels en de oude bewerkingsvolgorde MVDWOA tot aan het eind van de 20e eeuw (Sigma, laatste druk verschenen in de jaren 90).[6]
Nog ouder

Nog oudere algebraboeken laten zien dat de volgorde die Badon Ghijben optekende, bij zijn voorgangers inderdaad gangbaar was. Daarin komen de volgende, van de moderne volgorde afwijkende, gevallen voor (terloops in voorbeelden, zonder dat het als voorrangsregel geformuleerd werd):
- voorrang van vermenigvuldigen boven worteltrekken, zoals in , en
- voorrang van vermenigvuldigen boven delen, zoals in en .
Geval (1) is zichtbaar in alle oude algebraboeken[7][8][9][10][11][12][13] omdat de wortel van een product geschreven werd zonder bovenstreep; de bovenstreep werd slechts gebruikt voor de wortel van een veelterm, zoals in . Die gewoonte was afkomstig van Descartes[7]; de ondergeschiktheid van worteltrekken aan vermenigvuldigen in 'Meneer van Dalen wacht op antwoord' is dus te danken aan hem. De beperking op het gebruik van de bovenstreep was handig in de begintijd van de boekdrukkunst omdat de bovenstreep van de wortel problematisch zetwerk was: "het lyntje daarboven te stellen is niet alleen oorzaak dat de regels van ongelyke afstand worden, maar ook datze veeltyds scheef komen te staan, dat geen goede gestalte aan een boek geeft".[12] Geval (2) is iets zeldzamer omdat een expressie als in een minderheid van de oude algebraboeken voorkomt[12][13].
Minteken als unaire operatie
Het minteken als unaire operatie heeft een lagere prioriteit dan machtsverheffen, zodat −3² = −9 en . Er zijn echter enkele afwijkende applicaties en programmeertalen, met name Microsoft Excel en de programmeertaal bc, waarin het een hogere prioriteit heeft dan machtsverheffen, zodat daar −3² = 9.
Uitzondering op de regel
Vakgebieden met ingewikkelde formules en berekeningen, zoals natuurkunde, kunnen een traditie hebben van kleine uitzonderingen op de standaard bewerkingsvolgorde ten behoeve van de leesbaarheid. De uitzondering kan vastgelegd zijn in de stijlgids van belangrijke vaktijdschriften. Zo schrijft het natuurkundige tijdschrift Physical Review voor dat delen een lagere prioriteit heeft dan vermenigvuldigen indien de deling met een schuine breukstreep wordt geschreven.[14] Bijvoorbeeld in h/4π en e−t/RC.
6/2(1+2)=?

In 2011 ontstond er op internet een lawine van aandacht (internetmeme) voor het bewerkingsvolgordevraagstuk 6/2(1+2)=?.[15] Het werd als meerkeuzevraag op Facebook door miljoenen mensen beantwoord. De meningen bleken zeer verdeeld: de antwoorden 1 en 9 waren ongeveer even populair. De verklaring van deskundigen is dat notatie van breuken zoals , met een schuine breukstreep, inderdaad niet universeel eenduidig zijn. Deze notatie wordt daarom afgeraden.[16]
Wiskunde met logica
Volgorde:
- negatie ()
- conjunctie ()
- disjunctie ()
- implicatie (, , ) en equivalentie (, , )
De conventie is dat de implicatie rechts-associatief is, dat wil zeggen dat bij meerdere achter elkaar de laatste de hoogste prioriteit/binding heeft. De propositie betekent dus . Deze zijn overigens equivalent met .
Als er kwantoren in een uitdrukking voorkomen gaat het nog steeds om het ontleden van een geneste structuur, maar is er weliswaar een soort "bewerkingsvolgorde" van binnen naar buiten, maar wel met inachtneming van de domeinen van de kwantoren erbuiten, want die bepalen de waarden van de vrije variabelen in de binnenstructuur.
Voorbeeld met kwantoren:
Definitie: Het getal heet limiet van de rij getallen , als
- .
De kwantoren vormen unaire operatoren die zoals gebruikelijk vóór de operand staan. Als de operand zoals hier zelf alleen een kwantoruitdrukking is kunnen zonder dubbelzinnigheid haakjes weggelaten worden, en staat de binnenste kwantor achteraan. Dit is analoog aan onder meer de sommatienotatie.
Zie ook
Bronnen, noten en/of referenties
|