Hyperbool (meetkunde)

Hyperbool in het rood waarin ${\displaystyle c}$ (zie 'Vergelijkingen') gelijk is aan 8. De waarde voor ${\displaystyle a}$ is gelijk aan 2, het afstandsverschil is ${\displaystyle d=\operatorname {abs} (d_{2}-d_{1})=4.}$

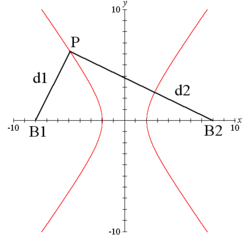
Men kan een hyperbool ook beschrijven als alle punten waarvoor het verschil van de afstanden ${\displaystyle d_{1}}$ en ${\displaystyle d_{2}}$ tot twee gekozen punten, de brandpunten, een constante waarde ${\displaystyle d}$ heeft. Een hyperbool bestaat daarom uit twee takken.

Een hyperbool heeft twee assen: de lijn door de twee brandpunten van de hyperbool heet de hoofdas en de lijn loodrecht daarop midden tussen de brandpunten (en midden tussen de takken van de hyperbool) heet de nevenas.

De assenrechthoek van een hyperbool is de rechthoek waarvan twee zijden raken aan de toppen van de takken van de hyperbool, en de hoekpunten op de asymptoten liggen. De diagonalen liggen op de asymptoten. De lengte van de diagonalen is gelijk aan de afstand tussen de brandpunten van de hyperbool.[2]

Als twee cirkels gegeven zijn met gelijke straal, kleiner dan de afstand van de middelpunten, dan vormen de beide conflictlijnen van de ene cirkel met het middelpunt van de andere cirkel een hyperbool. De middelpunten van de cirkels zijn de brandpunten; de cirkels worden richtcirkels genoemd. De conflictlijn bestaat uit alle punten waarvan de afstand tot de richtcirkel gelijk is aan de afstand tot het middelpunt van de andere richtcirkel.

Een hyperbool is de meetkundige plaats van de punten in het platte vlak waarbij de verhouding van de afstand tot een willekeurig punt, brandpunt geheten, tot de afstand tot een willekeurige rechte, richtlijn geheten, constant is. Deze constante verhouding heet de excentriciteit ${\displaystyle \varepsilon }$ van de hyperbool. Voor een hyperbool is ${\displaystyle \varepsilon >1}$. Met elk brandpunt correspondeert een richtlijn. De twee combinaties van een brandpunt en de bijbehorende (dichtbijzijnde) richtlijn leveren elk de complete hyperbool op.

Voor ${\displaystyle \varepsilon =1}$ wordt de figuur een parabool en voor ${\displaystyle 0<\varepsilon <1}$ een ellips.

De richtlijnen staan loodrecht op de hoofdas, op een afstand van ${\displaystyle {\frac {a}{\varepsilon }}}$ van de nevenas. De afstand van de hyperbool tot de dichtstbijzijnde richtlijn is ${\displaystyle a-{\frac {a}{\varepsilon }}}$, dit is voor ${\displaystyle \varepsilon \approx 1}$ ongeveer gelijk aan ${\displaystyle a\varepsilon -a}$. De afstand van het betreffende brandpunt tot de hyperbool is dan ook ongeveer hieraan gelijk. Als ${\displaystyle \varepsilon }$ van boven naar 1 nadert en ${\displaystyle a\varepsilon -a}$ gelijk gehouden wordt, en ${\displaystyle a}$ dus naar oneindig nadert, nadert de betreffende hyperbooltak in de buurt van het betreffende brandpunt en de betreffende richtlijn tot een parabool, met als as de hoofdas van de hyperbool. De nevenas en de andere tak verdwijnen, gezien vanuit de betreffende omgeving, naar het oneindige, de parabool heeft maar één as en één tak. De hoek tussen de asymptoten (met het hoekpunt ook steeds verder weg) gaat naar nul.

De punten ${\displaystyle (x,y)}$ op een hyperbool met het centrum in de oorsprong en waarvan de brandpunten in ${\displaystyle B_{1}=(-c,0)}$ en ${\displaystyle B_{2}=(c,0)}$ liggen, voldoen aan:

${\displaystyle \left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1}$;

daarin is:

${\displaystyle a^{2}+b^{2}=c^{2}}$

Verderop wordt een afleiding van deze vergelijking gegeven.

De hyperbool snijdt de x-as in de punten ${\displaystyle (-a,0)}$ en ${\displaystyle (a,0)}$, en voor de afstanden ${\displaystyle d_{1}}$ en ${\displaystyle d_{2}}$ van een punt op de hyperbool tot de brandpunten geldt:

${\displaystyle |d_{2}-d_{1}|=2a}$

Anders dan bij een ellips kan ${\displaystyle b}$ groter zijn dan ${\displaystyle a}$.

Een hyperbool wordt, bij geschikte keuze van het assenstelsel, beschreven door de volgende parametervergelijking:

${\displaystyle x=\pm \;a\cosh t}$

${\displaystyle y=b\sinh t}$,

waarbij gebruikgemaakt wordt van de hyperbolische functies (let op de naam!).

Er zijn meer definities in poolcoördinaten mogelijk:

${\displaystyle {\begin{array}{lrl}r^{2}=&a&\sec 2t\\r^{2}=&-a&\sec 2t\\r^{2}=&a&\csc 2t\\r^{2}=&-a&\csc 2t\\\end{array}}}$

Een hyperbool met

• hoofdas ${\displaystyle 2a}$,
• nevenas ${\displaystyle 2b}$,
• middelpunt in de oorsprong ${\displaystyle O}$ van een cartesisch coördinatenstelsel ${\displaystyle Oxy}$,
• brandpunten op de ${\displaystyle x}$-as,

voldoet aan de vergelijking:

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$

Dit is de middelpuntsvergelijking van de hyperbool.

Waar eerst ${\displaystyle d_{1}}$ en ${\displaystyle d_{2}}$ werden gebruikt, worden hier ${\displaystyle r_{1}}$ en ${\displaystyle r_{2}}$ gebruikt.

symbool	omschrijving
${\displaystyle \varepsilon }$	een willekeurige hyperbool in het platte vlak
${\displaystyle F_{1}}$, ${\displaystyle F_{2}}$	de brandpunten van ${\displaystyle \varepsilon }$
${\displaystyle Oxy}$	• een orthogonaal assenstelsel • met als oorsprong ${\displaystyle O}$ het midden van het lijnstuk ${\displaystyle F_{1}F_{2}}$ • de ${\displaystyle x}$-as wijst van ${\displaystyle F_{1}}$ naar ${\displaystyle F_{2}}$
${\displaystyle 2c}$	brandpuntsafstand van ${\displaystyle \varepsilon }$, per definitie de afstand tussen ${\displaystyle F_{1}}$ en ${\displaystyle F_{2}}$
${\displaystyle P}$	een willekeurig punt van ${\displaystyle \varepsilon }$
${\displaystyle x}$	de ${\displaystyle x}$-coördinaat van ${\displaystyle P}$
${\displaystyle y}$	de ${\displaystyle y}$-coördinaat van ${\displaystyle P}$
${\displaystyle r_{1}}$	de lengte van de voerstraal van ${\displaystyle P}$ vanuit ${\displaystyle F_{1}}$
${\displaystyle r_{2}}$	de lengte van de voerstraal van ${\displaystyle P}$ vanuit ${\displaystyle F_{2}}$
${\displaystyle 2a}$	de lengte van de hoofdas van ${\displaystyle \varepsilon }$
${\displaystyle 2b}$	de lengte van de nevenas van ${\displaystyle \varepsilon }$

stap	maak gebruik van	er geldt dan
${\displaystyle _{s.1}}$	definitie hyperbool	${\displaystyle _{r_{1}}}$${\displaystyle _{-}}$${\displaystyle _{r_{2}=}}$${\displaystyle _{^{\pm }}}$${\displaystyle _{2a}}$
${\displaystyle _{s.2}}$	stelling van Pythagoras	${\displaystyle _{r_{1}^{2}=(x+c)^{2}+y^{2}}}$
${\displaystyle _{s.3}}$	stelling van Pythagoras	${\displaystyle _{r_{2}^{2}=(x-c)^{2}+y^{2}}}$
${\displaystyle _{s.4}}$	${\displaystyle _{s.2-s.3}}$	${\displaystyle _{r_{1}^{2}-r_{2}^{2}=((x+c)^{2}+y^{2}))-((x-c)^{2}+y^{2}))}}$
${\displaystyle _{s.5}}$	${\displaystyle _{s.4}}$ • merkwaardig product	${\displaystyle _{(r_{1}+r_{2})(r_{1}-r_{2})=4cx}}$
${\displaystyle _{s.6}}$	${\displaystyle _{s.1}}$ ${\displaystyle _{s.5}}$	${\displaystyle _{^{\pm }}}$${\displaystyle _{2a(r_{1}}}$${\displaystyle _{+}}$${\displaystyle _{r_{2})=4cx}}$
${\displaystyle _{s.7}}$	${\displaystyle _{s.6}}$	${\displaystyle _{r_{1}}}$${\displaystyle _{+}}$${\displaystyle _{r_{2}=}}$${\displaystyle _{^{\pm }}}$${\displaystyle _{2cx/a}}$
${\displaystyle _{s.8}}$	${\displaystyle _{(s.1+s.7)/2}}$	${\displaystyle _{r_{1}=}}$${\displaystyle _{^{\pm }}}$(${\displaystyle _{a+cx/a}}$)
${\displaystyle _{s.9}}$	${\displaystyle _{-}}$${\displaystyle _{(s.1-s.7)/2}}$	${\displaystyle _{r_{2}=}}$${\displaystyle _{^{\mp }}}$(${\displaystyle _{a-cx/a}}$)

s.8 en s.9 gelden samen.

stap	maak gebruik van	er geldt dan
${\displaystyle _{s.10}}$	${\displaystyle _{(s.8)^{2}+(s.9)^{2}}}$	${\displaystyle _{r_{1}^{2}+r_{2}^{2}=(a+cx/a)^{2}+(a-cx/a)^{2}}}$
${\displaystyle _{s.11}}$	${\displaystyle _{s.10}}$ • merkwaardig product	${\displaystyle _{r_{1}^{2}+r_{2}^{2}=2(a^{2}+(cx/a)^{2})}}$
${\displaystyle _{s.12}}$	${\displaystyle _{s.2+s.3}}$	${\displaystyle _{r_{1}^{2}+r_{2}^{2}=(x+c)^{2}+(x-c)^{2}+2y^{2}}}$
${\displaystyle _{s.13}}$	${\displaystyle _{(s.11=s.12)/2}}$ • merkwaardig product	${\displaystyle _{a^{2}+(cx/a)^{2}=x^{2}+c^{2}+y^{2}}}$
${\displaystyle _{s.14}}$	${\displaystyle _{s.13}}$	${\displaystyle _{a^{2}=(1-(c/a)^{2})x^{2}+c^{2}+y^{2}}}$
${\displaystyle _{s.15}}$	${\displaystyle _{s.14}}$	${\displaystyle _{a^{2}-c^{2}=(1/a^{2})(a^{2}-c^{2})x^{2}+y^{2}}}$
${\displaystyle _{s.16}}$	betrekking tussen brandpuntsafstand, hoofdas en nevenas	${\displaystyle _{c^{2}=a^{2}}}$ ${\displaystyle _{+}}$ ${\displaystyle _{b^{2}}}$
${\displaystyle _{s.17}}$	${\displaystyle _{s.15}}$ ${\displaystyle _{s.16}}$	${\displaystyle _{b^{2}=(b^{2}/a^{2})x^{2}}}$${\displaystyle _{-}}$${\displaystyle _{y^{2}}}$
${\displaystyle _{s.18}}$	${\displaystyle _{(s.17)/b^{2}}}$	${\displaystyle _{x^{2}/a^{2}}}$${\displaystyle _{-}}$${\displaystyle _{y^{2}/b^{2}=1}}$

Nu is aangetoond dat als een punt ${\displaystyle P}$ op de hyperbool ligt, de coördinaten ${\displaystyle (x,y)}$ van ${\displaystyle P}$ voldoen aan de vergelijking ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$.

Omgekeerd kan men aantonen dat als de coördinaten ${\displaystyle (x,y)}$ van een willekeurig punt ${\displaystyle P}$ voldoen aan die vergelijking, ${\displaystyle P}$ op die hyperbool ligt.

Dus is ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$ de vergelijking van een hyperbool.