Tralie (wiskunde)
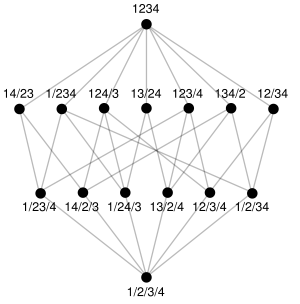
In de wiskunde is een tralie een partieel geordende verzameling waarin elke eindige deelverzameling zowel een supremum als een infimum heeft. De naam is afkomstig van de voorstelling van een tralie in een Hasse-diagram, waarin de in de ordening vergelijkbare elementen door een lijn zijn verbonden en het kleinere element lager geplaatst is dan het grotere. De zo ontstane figuur doet in sommige gevallen aan een traliewerk denken.
Definitie
Een tralie is een partieel geordende verzameling , waarin voor elk tweetal elementen en de verzameling zowel een supremum (= kleinste bovengrens) als een infimum (= grootste ondergrens) heeft.
Uit de definitie volgt direct dat elke eindige (niet-lege) deelverzameling ook een supremum en een infimum heeft.
Een tralie met zowel een grootste als een kleinste element, gewoonlijk aangeduid met respectievelijk 1 en 0, heet begrensd.
Door aan een partieel geordende verzameling een grootste en een kleinste element toe te voegen ontstaat een begrensde tralie.
Dualiteit
Door omkering van de ordening ontstaat uit een tralie een andere tralie, waarin als het ware de begrippen groter en kleiner omgewisseld zijn. Is een tralie, dan is ook er een.
Ordening
De ordening en de begrippen supremum en infimum zijn erg met elkaar verbonden. In feite leggen supremum en infimum de ordening vast. Als namelijk en beide tralies zijn, is , dat wil zeggen beide tralies hebben dezelfde partiële ordening. De ordening wordt immers bepaald door:
of equivalent door
Dus:
- .
Algebraïsche structuur
Doordat in een tralie bij elk tweetal elementen en de elementen en bestaan, zijn ("en") en ("of") binaire bewerkingen. Een tralie kan daarom ook opgevat worden als een algebraïsche structuur met deze beide bewerkingen.
Definitie
Een algebraïsche structuur , gevormd door een verzameling met daarop gedefinieerd twee binaire bewerkingen, ("of") en ("en") heet een tralie als voldaan is aan:
Van deze eigenschappen zijn associativiteit en commutativiteit tamelijk gewoon voor binaire bewerkingen. Het bijzondere schuilt hier in de eigenschap absorptie; deze bepaalt het karakter van de bewerkingen.
Idempotentie
Uit de absorptie-eigenschap volgt dat:
Immers, stel en , dan
en
- .
Dualiteit
Ook hier is sprake van dualiteit. Als een tralie is, is ook er een.
Voorbeeld
De machtsverzameling van een verzameling , dus de verzameling van alle deelverzamelingen van , is een tralie. In de zin van de eerste definitie is de ordening bepaald door het begrip deelverzameling, dus:
Supremum en infimum zijn vanzelfsprekend vereniging en doorsnede:
en
- .
De tralie is begrensd, met en .
Equivalentie van beide definities
Het is gemakkelijk te verifiëren dat de bewerkingen in een tralie volgens de eerste definitie voldoen aan de verlangde eisen in de tweede definitie. Omgekeerd kan een partiële ordening gedefinieerd worden in een tralie volgens de tweede definitie, door:
- als .
Dan is ook:
- dan en slechts dan als ,
want
- , dus
en
- , dus .
Het is niet moeilijk in te zien dat de zo bepaalde relatie inderdaad een partiële ordening op is. Verder is nu bij elk tweetal elementen en van het element het verlangde supremum en het verlangde infimum, immers vanwege de absorptie-eigenschappen is:
- , dus
- , dus .
en
- , dus
- , dus .
Dus is een majorant van en een minorant. Het zijn ook respectievelijk de kleinste en de grootste, want stel:
en
- ,
dan:
- .
En analoog, stel:
en
- ,
dan:
- .
We zien dus dat een tralie in de eerste zin ook een tralie in de tweede zin is en omgekeerd. Bovendien hebben we gezien dat als de bewerkingen in de algebraïsche tralie overeenkomen met die in de ordeningstralie, de door de bewerkingen geïnduceerde partiële ordening dezelfde is als de oorspronkelijke. Daarmee zijn de twee begrippen tralie geheel uitwisselbaar en kan al naargelang de toepassing de daartoe meest geschikte vorm gekozen worden.
Geschiedenis
Op het einde van de negentiende eeuw introduceerden Charles Sanders Peirce en Ernst Schröder het traliebegrip bij hun onderzoek naar de axiomatisering van Booleaanse algebras. Richard Dedekind kwam onafhankelijk van hen tot de ontdekking van hetzelfde begrip via zijn onderzoek naar idealen van algebraïsche getallen. Hun ideeën, evenmin als the vroege resultaten van Edward Huntington, trokken weinig aandacht. De algemene ontwikkeling van de tralietheorie begon met het werk van Garrett Birkhoff in het midden van de jaren 1930.[1]
Toepassingen
In de formeleconceptanalyse maakt men gebruikt van tralies voor het analyseren van gegevens die voorliggen als een binaire relatie: "object heeft eigenschap ".
Volledige tralie
Een tralie heet volledig, als iedere deelverzameling (ook de lege en eventueel oneindige) een supremum en een infimum heeft.
Het is voldoende voor elke deelverzameling het bestaan van het supremum te eisen, want
- .
Iedere volledige tralie is begrend, en iedere eindige niet-lege tralie is volledig en dus ook begrensd.
Bronnen, noten en/of referenties
|