Dichtste bolstapeling

In de meetkunde en kristallografie is de dichtste bolstapeling of dichtste stapeling van bollen, ook wel dichtste pakking genoemd, een zodanige configuratie, regelmatig of onregelmatig, van een oneindige verzameling van identieke bollen, dat geen andere configuratie meer ruimte van een oneindige driedimensionale ruimte inneemt.

Stapeling van bollen.
Dichtste stapeling van bollen opgebouwd uit ABAC-lagen.

Vullingsfactor

Onder de vullingsfactor of uitgebreider ruimtelijke vullingsfactor van een bolstapeling verstaat men de limietwaarde van verhouding van het volume van de bollen in een eindig deel van de ruimte en het volume van dat deel zelf. Men spreekt ook van gemiddelde dichtheid van de configuratie.

Carl Friedrich Gauss bewees dat de hoogste gemiddelde dichtheid of de hoogste vullingsfactor die door een regelmatige roosterschikking kan worden bereikt, gelijk is aan

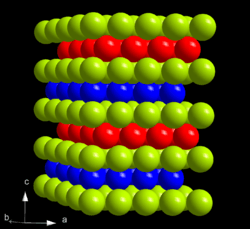
Deze zelfde pakkingsdichtheid kan ook worden bereikt door afwisselende stapelingen van dezelfde dichtst-gestapelde vlakken van bollen, waaronder structuren die aperiodiek in de stapelrichting zijn.

Het vermoeden van Kepler stelt dat ook de hoogste dichtheid is, die voor enige (regelmatige óf onregelmatige) roosterschikking van bollen kan worden bereikt. Dit vermoeden wordt nu algemeen beschouwd als in 1998 te zijn bewezen door Thomas Hales.[1][2][3]

Regelmatige stapelingen

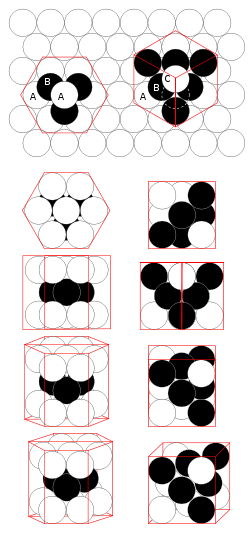
De bovengenoende bovengrens van de dichtheid wordt bereikt in twee regelmatige, iets verschillende stapelingen van drie opeenvolgende lagen: de hexagonale dichtste stapeling (hexagonal close-packed, hcp) en de kubisch vlakgecentreerde stapeling (face-centered cubic, fcc).

Als we ervan uitgaan dat de eerste laag, zoals aangegeven in de figuur rechts, op positie A ligt en de volgende laag op positie B, dan kan de volgende laag op twee verschillende posities op de tweede laag aangebracht worden: op positie A of op positie C. In het eerste geval kan de reeks voortgezet worden als een sequentie ABABA... In het andere geval volgt een sequentie ABCABCA...

  • De AB-stapeling bepaalt een rooster met een hexagonale symmetrie.
  • De ABC-stapeling bepaalt een rooster met kubische symmetrie.

Kristallografie

In de kristallografie worden dichtste bolstapelingen gevonden in de kristalstructuur van edelgassen en metalen. In veel gevallen komen zowel de kubische als de hexagonale structuur van hetzelfde element voor omdat het verschil in vrije energie tussen de verschillende metastabiele, allotrope kristalstructuren over het algemeen klein is.

Er komen echter ook reeksen voor met langere sequenties, zoals een opeenvolging van de reeks ABAC bij lanthaan, cerium en praseodymium. In kleine kristallen van kobalt worden random stapelingen aangetroffen.[4]

Zie ook

Referentie
  1. Thomas Hales, arXiv,eprint=math/9811071, An overview of the Kepler conjecture, 1998, v2
  2. Mathematics: Does the proof stack up?.
  3. Sally Pobojewski, Hales solves oldest problem in discrete geometry
  4. C. Kittel, Introduction to Solid State Physics. Wiley & Sons (1953-1976). ISBN 0-471-49024-5.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.