Partitie (getaltheorie)

In de getaltheorie is een partitie van een positief natuurlijk getal een manier om dat getal te schrijven als een som van positieve natuurlijke getallen. Het aantal partities van $n$ wordt gegeven door de partitiefunctie $p(n).$

Ferrersdiagram met de partities van de getallen 1 tot 8

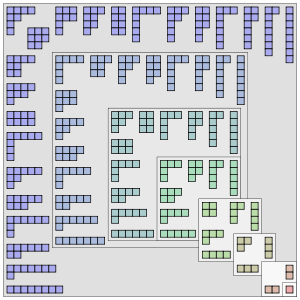
Een Ferrersdiagram is de grafische voorstelling van een partitie van een getal.

Voorbeelden

Partities van het getal 4

$\quad$ 4
$\quad$ 3 + 1
$\quad$ 2 + 2
$\quad$ 2 + 1 + 1
$\quad$ 1 + 1 + 1 + 1

Groepentheorie

Het is in de groepentheorie gegeven dat iedere conjugatieklasse in de symmetrische groep door het cykeltype van de elementen binnen die conjugatieklasse is bepaald. Het aantal conjugatieklassen in de symmetrische groep $S(n)$ is dus gelijk aan het aantal partities van het getal $n.$

partities van 7
	cykeltype	aantal[1]
1	1 1 1 1 1 1 1	1
2	2 1 1 1 1 1	21
3	3 1 1 1 1	70
4	2 2 1 1 1	105
5	4 1 1 1	210
6	3 2 1 1	420
7	5 1 1	504
8	2 2 2 1	105
9	4 2 1	630
10	3 3 1	280
11	6 1	840
12	3 2 2	210
13	5 2	504
14	4 3	420
15	7	720
		5040

Partitiefunctie

De partitiefunctie $p(n)$ is gelijk aan het aantal mogelijke partities van het getal $n.$ Bijvoorbeeld is $p(4)=5.$ Per definitie is $p(0)=1$ . Voor het gemak definieert men ook $p(n)=0$ voor negatieve gehele getallen $n.$

Waarden

p(1) = 1
p(2) = 2
p(3) = 3
p(4) = 5
p(5) = 7
p(6) = 11
p(7) = 15
p(8) = 22
p(9) = 30
p(10) = 42
p(100) = 190.569.292
p(200) = 3.972.999.029.388
p(1000) = 24.061.467.864.032.622.473.692.149.727.991 ≈ 2,4 × 10³¹

Srinivasa Aaiyangar Ramanujan heeft in de partitiefunctie een aantal congruenties ontdekt. Voor elke gehele $k$ geldt

p(5k+4)\equiv 0{\pmod {5}}

p(7k+5)\equiv 0{\pmod {7}}

p(11k+6)\equiv 0{\pmod {11}}

Voortbrengende functie

De voortbrengende functie voor $p(n)$ is, zoals bewezen door Euler:

\sum _{n=0}^{\infty }p(n)x^{n}=\prod _{k=1}^{\infty }\left({\frac {1}{1-x^{k}}}\right).

Elke factor in dit product kan worden beschouwd als de som van een meetkundige rij, zodat men het kan uitwerken als:

(1+x+x^{2}+x^{3}+\ldots )(1+x^{2}+x^{4}+x^{6}+\ldots )(1+x^{3}+x^{6}+x^{9}+\ldots )\ldots =

=1+x+2x^{2}+3x^{3}+5x^{4}+7x^{5}+\ldots

Intermediaire partitiefunctie

De intermediaire partitiefunctie $p(k,n)$ is het aantal partities die alleen maar getallen gebruikt die groter of gelijk zijn aan $k.$ Hier enkele voorbeelden:

p(1, 4) = 5
p(2, 8) = 7
p(3, 12) = 9
p(4, 16) = 11
p(5, 20) = 13
p(6, 24) = 16

De originele partitiefunctie $p(n)$ is dus $p(1,n).$

Hier volgt een tabel met waarden van $p(k,n)$ :

		k
		1	2	3	4	5	6	7	8	9	10
n	1	1	0	0	0	0	0	0	0	0	0
	2	2	1	0	0	0	0	0	0	0	0
	3	3	1	1	0	0	0	0	0	0	0
	4	5	2	1	1	0	0	0	0	0	0
	5	7	2	1	1	1	0	0	0	0	0
	6	11	4	2	1	1	1	0	0	0	0
	7	15	4	2	1	1	1	1	0	0	0
	8	22	7	3	2	1	1	1	1	0	0
	9	30	8	4	2	1	1	1	1	1	0
	10	42	12	5	3	2	1	1	1	1	1

Partities met voorwaarden

Van de 22 partities voor het getal 8 zijn er 6 partities met alleen oneven getallen:

7 + 1
5 + 3
5 + 1 + 1 + 1
3 + 3 + 1 + 1
3 + 1 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Het aantal partities van 8 met alleen verschillende getallen is eveneens gelijk aan 6:

8
7 + 1
6 + 2
5 + 3
5 + 2 + 1
4 + 3 + 1

Leonhard Euler toonde in 1748 aan dat voor alle natuurlijke getallen het aantal partities met oneven getallen altijd gelijk is aan het aantal partities met verschillende getallen.[2]

H Hofstede Uit Hoeveel sommen komt 20? over de berekening van het aantal partities van een getal

Het aantal conjugatieklassen in de symmetrische groep $S(7)$ met het gegeven cykeltype
(en) GE Andrews Number Theory, 1971. blz 149–150.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Het aantal conjugatieklassen in de symmetrische groep $S(7)$ met het gegeven cykeltype

[2] (en) GE Andrews Number Theory, 1971. blz 149–150.