Ornstein–Uhlenbeck process

A temporally homogeneous Ornstein–Uhlenbeck process can be represented as a scaled, time-transformed Wiener process:

${\displaystyle x_{t}={\frac {\sigma }{\sqrt {2\theta }}}e^{-\theta t}W_{e^{2\theta t}}}$

where ${\displaystyle W_{t}}$ is the standard Wiener process.[1] Equivalently, with the change of variable ${\displaystyle s=e^{2\theta t}}$ this becomes

${\displaystyle W_{s}={\frac {\sqrt {2\theta }}{\sigma }}s^{1/2}x_{(\ln s)/(2\theta )},\qquad s>0}$

Using this mapping, one can translate known properties of ${\displaystyle W_{t}}$ into corresponding statements for ${\displaystyle x_{t}}$. For instance, the law of the iterated logarithm for ${\displaystyle W_{t}}$ becomes[1]

${\displaystyle \lim _{t\rightarrow 0}\sup {\frac {x_{t}}{\sqrt {(\sigma ^{2}/\theta )\ln t}}}=1,\quad {\text{with probability 1.}}}$

The stochastic differential equation for ${\displaystyle x_{t}}$ can be formally solved by variation of parameters.[9] Writing

${\displaystyle f(x_{t},t)=x_{t}e^{\theta t}\,}$

we get

${\displaystyle {\begin{aligned}df(x_{t},t)&=\theta \,x_{t}\,e^{\theta t}\,dt+e^{\theta t}\,dx_{t}\\[6pt]&=e^{\theta t}\theta \,\mu \,dt+\sigma \,e^{\theta t}\,dW_{t}.\end{aligned}}}$

Integrating from ${\displaystyle 0}$ to ${\displaystyle t}$ we get

${\displaystyle x_{t}e^{\theta t}=x_{0}+\int _{0}^{t}e^{\theta s}\theta \,\mu \,ds+\int _{0}^{t}\sigma \,e^{\theta s}\,dW_{s}\,}$

whereupon we see

${\displaystyle x_{t}=x_{0}\,e^{-\theta t}+\mu \,(1-e^{-\theta t})+\sigma \int _{0}^{t}e^{-\theta (t-s)}\,dW_{s}.\,}$

From this representation, the first moment (i.e. the mean) is shown to be

${\displaystyle \operatorname {E} (x_{t})=x_{0}e^{-\theta t}+\mu (1-e^{-\theta t})\!\ }$

assuming ${\displaystyle x_{0}}$ is constant. Moreover, the Itō isometry can be used to calculate the covariance function by

${\displaystyle {\begin{aligned}\operatorname {cov} (x_{s},x_{t})&=\operatorname {E} [(x_{s}-\operatorname {E} [x_{s}])(x_{t}-\operatorname {E} [x_{t}])]\\[5pt]&=\operatorname {E} \left[\int _{0}^{s}\sigma e^{\theta (u-s)}\,dW_{u}\int _{0}^{t}\sigma e^{\theta (v-t)}\,dW_{v}\right]\\[5pt]&=\sigma ^{2}e^{-\theta (s+t)}\operatorname {E} \left[\int _{0}^{s}e^{\theta u}\,dW_{u}\int _{0}^{t}e^{\theta v}\,dW_{v}\right]\\[5pt]&={\frac {\sigma ^{2}}{2\theta }}\,e^{-\theta (s+t)}(e^{2\theta \min(s,t)}-1)\\[5pt]&={\frac {\sigma ^{2}}{2\theta }}\left(e^{-\theta |t-s|}-e^{-\theta (t+s)}\right).\end{aligned}}}$

By using discretely sampled data at time intervals of width ${\displaystyle t}$, the maximum likelihood estimators for the parameters of the Ornstein–Uhlenbeck process are asymptotically normal to their true values.[10] More precisely,

${\displaystyle {\sqrt {n}}\left({\begin{pmatrix}{\widehat {\theta }}_{n}\\{\widehat {\mu }}_{n}\\{\widehat {\sigma }}_{n}\end{pmatrix}}-{\begin{pmatrix}\theta \\\mu \\\sigma \end{pmatrix}}\right){\xrightarrow {d}}\ {\mathcal {N}}\left({\begin{pmatrix}0\\0\\0\end{pmatrix}},{\begin{pmatrix}{\frac {e^{2t\theta }-1}{t^{2}}}&0&{\frac {\sigma ^{2}(e^{2t\theta }-1-2t\theta )}{t^{2}\theta }}\\0&{\frac {\sigma ^{2}\left(e^{t\theta }+1\right)}{2\left(e^{t\theta }-1\right)\theta }}&0\\{\frac {\sigma ^{2}(e^{2t\theta }-1-2t\theta )}{t^{2}\theta }}&0&{\frac {\sigma ^{4}\left[\left(e^{2t\theta }-1\right)^{2}+2t^{2}\theta ^{2}\left(e^{2t\theta }+1\right)+4t\theta \left(e^{2t\theta }-1\right)\right]}{t^{2}\left(e^{2t\theta }-1\right)\theta ^{2}}}\end{pmatrix}}\right)}$

three sample paths of different OU-processes with θ = 1, μ = 1.2, σ = 0.3:
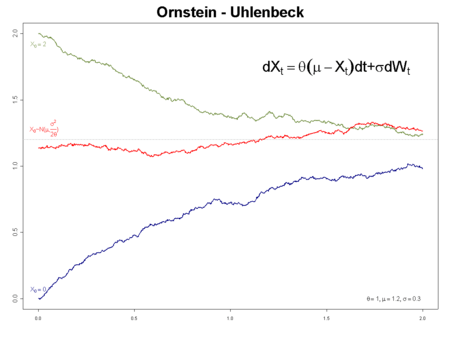
blue: initial value a = 0 (a.s.)
green: initial value a = 2 (a.s.)
red: initial value normally distributed so that the process has invariant measure

A multi-dimensional version of the Ornstein–Uhlenbeck process, denoted by the N-dimensional vector ${\displaystyle \mathbf {x} _{t}}$, can be defined from

${\displaystyle d\mathbf {x} _{t}=-{\boldsymbol {\beta }}\,\mathbf {x} _{t}\,dt+{\boldsymbol {\sigma }}\,d\mathbf {W} _{t}.}$

where ${\displaystyle \mathbf {W} _{t}}$ is an N-dimensional Wiener process, and ${\displaystyle {\boldsymbol {\beta }}}$ and ${\displaystyle {\boldsymbol {\sigma }}}$ are constant N×N matrices.[16] The solution is

${\displaystyle \mathbf {x} _{t}=e^{-{\boldsymbol {\beta }}t}\mathbf {x} _{0}+\int _{0}^{t}e^{-{\boldsymbol {\beta }}(t-t')}{\boldsymbol {\sigma }}\,d\mathbf {W} _{t'}}$

and the mean is

${\displaystyle \operatorname {E} (\mathbf {x} _{t})=e^{-{\boldsymbol {\beta }}t}\operatorname {E} (\mathbf {x} _{0}).}$

Note that these expressions make use of the matrix exponential.

The process can also be described in terms of the probability density function ${\displaystyle P(\mathbf {x} ,t)}$, which satisfies the Fokker–Planck equation[17]

${\displaystyle {\frac {\partial P}{\partial t}}=\sum _{i,j}\beta _{ij}{\frac {\partial }{\partial x_{i}}}(x_{j}P)+\sum _{i,j}D_{ij}{\frac {\partial ^{2}P}{\partial x_{i}\,\partial x_{j}}}.}$

where the matrix ${\displaystyle {\boldsymbol {D}}}$ with components ${\displaystyle D_{ij}}$ is defined by ${\displaystyle {\boldsymbol {D}}={\boldsymbol {\sigma }}{\boldsymbol {\sigma }}^{T}/2}$. As for the 1d case, the process is a linear transformation of Gaussian random variables, and therefore itself must be Gaussian. Because of this, the transition probability ${\displaystyle P(\mathbf {x} ,t\mid \mathbf {x} ',t')}$ is a Gaussian which can be written down explicitly. If the real parts of the eigenvalues of ${\displaystyle {\boldsymbol {\beta }}}$ are larger than zero, a stationary solution ${\displaystyle P_{\text{st}}(\mathbf {x} )}$ moreover exists, given by

${\displaystyle P_{\text{st}}(\mathbf {x} )=(2\pi )^{-N/2}(\det {\boldsymbol {\omega }})^{-1/2}\exp \left(-{\frac {1}{2}}\mathbf {x} ^{T}{\boldsymbol {\omega }}^{-1}\mathbf {x} \right)}$

where the matrix ${\displaystyle {\boldsymbol {\omega }}}$ is determined from ${\displaystyle {\boldsymbol {\beta }}{\boldsymbol {\omega }}+{\boldsymbol {\omega }}{\boldsymbol {\beta }}^{T}=2{\boldsymbol {D}}}$.[18]