Temperature
Temperature is a physical property of matter that quantitatively expresses hot and cold. It is the manifestation of thermal energy, present in all matter, which is the source of the occurrence of heat, a flow of energy, when a body is in contact with another that is colder.
| Temperature | |
|---|---|
 Two thermometers showing temperature in Celsius and Fahrenheit. | |
Common symbols | T |
| SI unit | K |
Other units | °C, °F, °R |
| Intensive? | Yes |
Derivations from other quantities | , |
| Dimension | Θ |

| Thermodynamics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 The classical Carnot heat engine | ||||||||||||
|
||||||||||||
| ||||||||||||
Temperature is measured with a thermometer. Thermometers are calibrated in various temperature scales that historically have used various reference points and thermometric substances for definition. The most common scales are the Celsius scale (formerly called centigrade, denoted °C), the Fahrenheit scale (denoted °F), and the Kelvin scale (denoted K), the last of which is predominantly used for scientific purposes by conventions of the International System of Units (SI).
The lowest theoretical temperature is absolute zero, at which no more thermal energy can be extracted from a body. Experimentally, it can only be approached very closely, but not reached, which is recognized in the third law of thermodynamics.
Temperature is important in all fields of natural science, including physics, chemistry, Earth science, medicine, and biology, as well as most aspects of daily life.
Effects
Many physical processes are related to temperature, such as:
- the physical properties of materials including the phase (solid, liquid, gaseous or plasma), density, solubility, vapor pressure, electrical conductivity,
- the rate and extent to which chemical reactions occur,[1]
- the amount and properties of thermal radiation emitted from the surface of an object, and
- the speed of sound which is a function of the square root of the absolute temperature.[2]
Scales
Temperature scales differ in two ways: the point chosen as zero degrees, and the magnitudes of incremental units or degrees on the scale.
Commonly used scales
The Celsius scale (°C) is used for common temperature measurements in most of the world. It is an empirical scale that was developed by a historical progress, which led to its zero point 0 °C being defined by the freezing point of water, and additional degrees defined so that 100 °C was the boiling point of water, both at sea-level atmospheric pressure. Because of the 100-degree interval, it was called a centigrade scale.[3] Since the standardization of the kelvin in the International System of Units, it has subsequently been redefined in terms of the equivalent fixing points on the Kelvin scale, and so that a temperature increment of one degree Celsius is the same as an increment of one kelvin, though they differ by an additive offset of approximately 273.15.
The United States commonly uses the Fahrenheit scale, on which water freezes at 32 °F and boils at 212 °F at sea-level atmospheric pressure.
Absolute zero
At the absolute zero of temperature, no more energy can be removed from matter as heat, a fact expressed in the third law of thermodynamics. At this temperature, matter contains no macroscopic thermal energy, but still has quantum-mechanical zero-point energy as predicted by the uncertainty principle. This does not enter into the definition of absolute temperature. Experimentally, absolute zero can only be approached very closely, but can never be actually reached. If it were possible to cool a system to absolute zero, all classical motion of its particles would cease and they would be at complete rest in this classical sense. The absolute zero, defined as 0 K, is approximately equal to −273.15 °C, or −459.67 °F.
Absolute scales
Referring to the Boltzmann constant, to the Maxwell–Boltzmann distribution, and to the Boltzmann statistical mechanical definition of entropy, as distinct from the Gibbs definition,[4] for independently moving microscopic particles, disregarding interparticle potential energy, by international agreement, a temperature scale is defined and said to be absolute because it is independent of the characteristics of particular thermometric substances and thermometer mechanisms. Apart from the absolute zero, it does not have a reference temperature. It is known as the Kelvin scale, widely used in science and technology. The kelvin (the word is spelled with a lower-case k) is the unit of temperature in the International System of Units (SI). The temperature of a body in its own state of thermodynamic equilibrium is always positive, relative to the absolute zero.
Besides the internationally agreed Kelvin scale, there is also a thermodynamic temperature scale, invented by Kelvin, also with its numerical zero at the absolute zero of temperature, but directly relating to purely macroscopic thermodynamic concepts, including the macroscopic entropy, though microscopically referable to the Gibbs statistical mechanical definition of entropy for the canonical ensemble, that takes interparticle potential energy into account, as well as independent particle motion, so that it can account for measurements of temperatures near absolute zero.[4] This scale has a reference temperature at the triple point of water, the numerical value of which is defined by measurements using the aforementioned internationally agreed Kelvin scale.
International Kelvin scale
Many scientific measurements use the Kelvin temperature scale (unit symbol: K), named in honor of the physicist who first defined it. It is an absolute scale. Its numerical zero point, 0 K, is at the absolute zero of temperature. Since May, 2019, its degrees have been defined through particle kinetic theory, and statistical mechanics. In the International System of Units (SI), the magnitude of the kelvin is defined through various empirical measurements of the average kinetic energies of microscopic particles. It is numerically evaluated in terms of the Boltzmann constant, the value of which is defined as fixed by international convention.[5][6]
Statistical mechanical versus thermodynamic temperature scales
Since May 2019, the magnitude of the kelvin is defined in relation to microscopic phenomena, characterized in terms of statistical mechanics. Previously, since 1954, the International System of Units defined a scale and unit for the kelvin as a thermodynamic temperature, by using the reliably reproducible temperature of the triple point of water as a second reference point, the first reference point being 0 K at absolute zero.
Historically, the triple point temperature of water was defined as exactly 273.16 units of the measurement increment. Today it is an empirically measured quantity. The freezing point of water at sea-level atmospheric pressure occurs at approximately 273.15 K = 0 °C.
Classification of scales
There is a variety of kinds of temperature scale. It may be convenient to classify them as empirically and theoretically based. Empirical temperature scales are historically older, while theoretically based scales arose in the middle of the nineteenth century.[7][8]
Empirical scales
Empirically based temperature scales rely directly on measurements of simple macroscopic physical properties of materials. For example, the length of a column of mercury, confined in a glass-walled capillary tube, is dependent largely on temperature, and is the basis of the very useful mercury-in-glass thermometer. Such scales are valid only within convenient ranges of temperature. For example, above the boiling point of mercury, a mercury-in-glass thermometer is impracticable. Most materials expand with temperature increase, but some materials, such as water, contract with temperature increase over some specific range, and then they are hardly useful as thermometric materials. A material is of no use as a thermometer near one of its phase-change temperatures, for example its boiling-point.
In spite of these limitations, most generally used practical thermometers are of the empirically based kind. Especially, it was used for calorimetry, which contributed greatly to the discovery of thermodynamics. Nevertheless, empirical thermometry has serious drawbacks when judged as a basis for theoretical physics. Empirically based thermometers, beyond their base as simple direct measurements of ordinary physical properties of thermometric materials, can be re-calibrated, by use of theoretical physical reasoning, and this can extend their range of adequacy.
Theoretical scales
Theoretically based temperature scales are based directly on theoretical arguments, especially those of kinetic theory and thermodynamics. They are more or less ideally realised in practically feasible physical devices and materials. Theoretically based temperature scales are used to provide calibrating standards for practical empirically based thermometers.
Microscopic statistical mechanical scale
In physics, the internationally agreed conventional temperature scale is called the Kelvin scale. It is calibrated through the internationally agreed and prescribed value of the Boltzmann constant,[5][6] referring to motions of microscopic particles, such as atoms, molecules, and electrons, constituent in the body whose temperature is to be measured. In contrast with the thermodynamic temperature scale invented by Kelvin, the presently conventional Kelvin temperature is not defined through comparison with the temperature of a reference state of a standard body, nor in terms of macroscopic thermodynamics.
Apart from the absolute zero of temperature, Kelvin temperature of a body in a state of internal thermodynamic equilibrium is defined by measurements of suitably chosen of its physical properties, such as have precisely known theoretical explanations in terms of the Boltzmann constant. That constant refers to chosen kinds of motion of microscopic particles in the constitution of the body. In those kinds of motion, the particles move individually, without mutual interaction. Such motions are typically interrupted by inter-particle collisions, but for temperature measurement, the motions are chosen so that, between collisions, the non-interactive segments of their trajectories are known to be accessible to accurate measurement. For this purpose, interperticle potential energy is disregarded.
In an ideal gas, and in other theoretically understood bodies, the Kelvin temperature is defined to be proportional to the average kinetic energy of non-interactively moving microscopic particles, which can be measured by suitable techniques. The proportionality constant is a simple multiple of the Boltzmann constant. If molecules, atoms, or electrons,[9][10] are emitted from a material and their velocities are measured, the spectrum of their velocities often nearly obeys a theoretical law called the Maxwell–Boltzmann distribution, which gives a well-founded measurement of temperatures for which the law holds.[11] There have not yet been successful experiments of this same kind that directly use the Fermi–Dirac distribution for thermometry, but perhaps that will be achieved in future.[12]
The speed of sound in a gas can be calculated theoretically from the molecular character of the gas, from its temperature and pressure, and from the value of Boltzmann's constant. For a gas of known molecular character and pressure, this provides a relation between temperature and Boltzmann's constant. Those quantities can be known or measured more precisely than can the thermodynamic variables that define the state of a sample of water at its triple point. Consequently, taking the value of Boltzmann's constant as a primarily defined reference of exactly defined value, a measurement of the speed of sound can provide a more precise measurement of the temperature of the gas.[13]
Measurement of the spectrum of electromagnetic radiation from an ideal three-dimensional black body can provide an accurate temperature measurement because the frequency of maximum spectral radiance of black-body radiation is directly proportional to the temperature of the black body; this is known as Wien's displacement law and has a theoretical explanation in Planck's law and the Bose–Einstein law.
Measurement of the spectrum of noise-power produced by an electrical resistor can also provide an accurate temperature measurement. The resistor has two terminals and is in effect a one-dimensional body. The Bose-Einstein law for this case indicates that the noise-power is directly proportional to the temperature of the resistor and to the value of its resistance and to the noise band-width. In a given frequency band, the noise-power has equal contributions from every frequency and is called Johnson noise. If the value of the resistance is known then the temperature can be found.[14][15]
Macroscopic thermodynamic scale
Historically, till May 2019, the definition of the Kelvin scale was that invented by Kelvin, based on a ratio of quantities of energy in processes in an ideal Carnot engine, entirely in terms of macroscopic thermodynamics. That Carnot engine was to work between two temperatures, that of the body whose temperature was to be measured, and a reference, that of a body at the temperature of the triple point of water. Then the reference temperature, that of the triple point, was defined to be exactly 273.16 K. Since May 2019, that value has not been fixed by definition, but is to be measured through microscopic phenomena, involving the Boltzmann constant, as described above. The microscopic statistical mechanical definition does not have a reference temperature.
Ideal gas
A material on which a macroscopically defined temperature scale may be based is the ideal gas. The pressure exerted by a fixed volume and mass of an ideal gas is directly proportional to its temperature. Some natural gases show so nearly ideal properties over suitable temperature ranges that they can be used for thermometry; this was important during the development of thermodynamics and is still of practical importance today.[16][17] The ideal gas thermometer is, however, not theoretically perfect for thermodynamics. This is because the entropy of an ideal gas at its absolute zero of temperature is not a positive semi-definite quantity, which puts the gas in violation of the third law of thermodynamics. In contrast to real materials, the ideal gas does not liquefy or solidify, no matter how cold it is. Alternatively thinking, the ideal gas law, refers to the limit of infinitely high temperature and zero pressure; these conditions guarantee non-interactive motions of the constituent molecules.[18][19][20]
Kinetic theory approach
The magnitude of the kelvin is now defined in terms of kinetic theory, derived from the value of Boltzmann's constant.
Kinetic theory provides a microscopic account of temperature for some bodies of material, especially gases, based on macroscopic systems' being composed of many microscopic particles, such as molecules and ions of various species, the particles of a species being all alike. It explains macroscopic phenomena through the classical mechanics of the microscopic particles. The equipartition theorem of kinetic theory asserts that each classical degree of freedom of a freely moving particle has an average kinetic energy of kBT/2 where kB denotes Boltzmann's constant. The translational motion of the particle has three degrees of freedom, so that, except at very low temperatures where quantum effects predominate, the average translational kinetic energy of a freely moving particle in a system with temperature T will be 3kBT/2.
Molecules, such as oxygen (O2), have more degrees of freedom than single spherical atoms: they undergo rotational and vibrational motions as well as translations. Heating results in an increase in temperature due to an increase in the average translational kinetic energy of the molecules. Heating will also cause, through equipartitioning, the energy associated with vibrational and rotational modes to increase. Thus a diatomic gas will require more energy input to increase its temperature by a certain amount, i.e. it will have a greater heat capacity than a monatomic gas.
As noted above, the speed of sound in a gas can be calculated from the molecular character of the gas, from its temperature and pressure, and from the value of Boltzmann's constant. Taking the value of Boltzmann's constant as a primarily defined reference of exactly defined value, a measurement of the speed of sound can provide a more precise measurement of the temperature of the gas.[13]
It is possible to measure the average kinetic energy of constituent microscopic particles if they are allowed to escape from the bulk of the system, through a small hole in the containing wall. The spectrum of velocities has to be measured, and the average calculated from that. It is not necessarily the case that the particles that escape and are measured have the same velocity distribution as the particles that remain in the bulk of the system, but sometimes a good sample is possible.
Thermodynamic approach
Temperature is one of the principal quantities in the study of thermodynamics. Formerly, the magnitude of the kelvin was defined in thermodynamic terms, but nowadays, as mentioned above, it is defined in terms of kinetic theory.
The thermodynamic temperature is said to be absolute for two reasons. One is that its formal character is independent of the properties of particular materials. The other reason is that its zero is, in a sense, absolute, in that it indicates absence of microscopic classical motion of the constituent particles of matter, so that they have a limiting specific heat of zero for zero temperature, according to the third law of thermodynamics. Nevertheless, a thermodynamic temperature does in fact have a definite numerical value that has been arbitrarily chosen by tradition and is dependent on the property of a particular materials; it is simply less arbitrary than relative "degrees" scales such as Celsius and Fahrenheit. Being an absolute scale with one fixed point (zero), there is only one degree of freedom left to arbitrary choice, rather than two as in relative scales. For the Kelvin scale since May 2019, by international convention, the choice has been made to use knowledge of modes of operation of various thermometric devices, relying on microscopic kinetic theories about molecular motion. The numerical scale is settled by a conventional definition of the value of the Boltzmann constant, which relates macroscopic temperature to average microscopic kinetic energy of particles such as molecules. Its numerical value is arbitrary, and an alternate, less widely used absolute temperature scale exists called the Rankine scale, made to be aligned with the Fahrenheit scale as Kelvin is with Celsius.
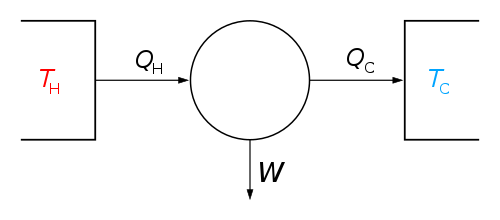
The thermodynamic definition of temperature is due to Kelvin. It is framed in terms of an idealized device called a Carnot engine, imagined to run in a fictive continuous cycle of successive processes that traverse a cycle of states of its working body. The engine takes in a quantity of heat Q1 from a hot reservoir and passes out a lesser quantity of heat Q2 to a cold reservoir. The difference in energy is passed, as thermodynamic work, to a work reservoir, and is considered to be the output of the engine. The cycle is imagined to run so slowly that at each point of the cycle the working body is in a state of thermodynamic equilibrium. The successive processes the cycle are thus imagined to run reversibly with no entropy production. Then the quantity of entropy taken in from the hot reservoir when the working body is heated is equal to that passed to the cold reservoir when the working body is cooled. Then the absolute or thermodynamic temperatures, T1 and T2, of the reservoirs are defined so that to be such that
-
(1)
The zeroth law of thermodynamics allows this definition to be used to measure the absolute or thermodynamic temperature of an arbitrary body of interest, by making the other heat reservoir have the same temperature as the body of interest.
Kelvin's original work postulating absolute temperature was published in 1848. It was based on the work of Carnot, before the formulation of the first law of thermodynamics. Carnot had no sound understanding of heat, and no specific concept of entropy. He wrote of 'caloric', and said that all the caloric that passed from the hot reservoir was passed into the cold reservoir. Kelvin wrote in his 1848 paper that his scale was absolute in the sense that it was defined "independently of the properties of any particular kind of matter". His definitive publication, which sets out the definition just stated, was printed in 1853, a paper read in 1851.[21][22][23][24]
Numerical details were formerly settled by making one of the heat reservoirs a cell at the triple point of water, which was defined to have an absolute temperature of 273.16 K.[25] Nowadays, the numerical value is instead obtained from measurement through the microscopic statistical mechanical international definition, as above.
Intensive variability
In thermodynamic terms, temperature is an intensive variable because it is equal to a differential coefficient of one extensive variable with respect to another, for a given body. It thus has the dimensions of a ratio of two extensive variables. In thermodynamics, two bodies are often considered as connected by contact with a common wall, which has some specific permeability properties. Such specific permeability can be referred to a specific intensive variable. An example is a diathermic wall that is permeable only to heat; the intensive variable for this case is temperature. When the two bodies have been in contact for a very long time, and have settled to a permanent steady state, the relevant intensive variables are equal in the two bodies; for a diathermal wall, this statement is sometimes called the zeroth law of thermodynamics.[26][27][28]
In particular, when the body is described by stating its internal energy U, an extensive variable, as a function of its entropy S, also an extensive variable, and other state variables V, N, with U = U (S, V, N), then the temperature is equal to the partial derivative of the internal energy with respect to the entropy:[27][28][29]
-
(2)
Likewise, when the body is described by stating its entropy S as a function of its internal energy U, and other state variables V, N, with S = S (U, V, N), then the reciprocal of the temperature is equal to the partial derivative of the entropy with respect to the internal energy:[27][29][30]
-
(3)
The above definition, equation (1), of the absolute temperature is due to Kelvin. It refers to systems closed to transfer of matter, and has special emphasis on directly experimental procedures. A presentation of thermodynamics by Gibbs starts at a more abstract level and deals with systems open to the transfer of matter; in this development of thermodynamics, the equations (2) and (3) above are actually alternative definitions of temperature.[31]
Local thermodynamic equilibrium
Real world bodies are often not in thermodynamic equilibrium and not homogeneous. For study by methods of classical irreversible thermodynamics, a body is usually spatially and temporally divided conceptually into 'cells' of small size. If classical thermodynamic equilibrium conditions for matter are fulfilled to good approximation in such a 'cell', then it is homogeneous and a temperature exists for it. If this is so for every 'cell' of the body, then local thermodynamic equilibrium is said to prevail throughout the body.[32][33][34][35][36]
It makes good sense, for example, to say of the extensive variable U, or of the extensive variable S, that it has a density per unit volume, or a quantity per unit mass of the system, but it makes no sense to speak of density of temperature per unit volume or quantity of temperature per unit mass of the system. On the other hand, it makes no sense to speak of the internal energy at a point, while when local thermodynamic equilibrium prevails, it makes good sense to speak of the temperature at a point. Consequently, temperature can vary from point to point in a medium that is not in global thermodynamic equilibrium, but in which there is local thermodynamic equilibrium.
Thus, when local thermodynamic equilibrium prevails in a body, temperature can be regarded as a spatially varying local property in that body, and this is because temperature is an intensive variable.
Basic theory
Temperature is a measure of a quality of a state of a material.[37] The quality may be regarded as a more abstract entity than any particular temperature scale that measures it, and is called hotness by some writers.[38] The quality of hotness refers to the state of material only in a particular locality, and in general, apart from bodies held in a steady state of thermodynamic equilibrium, hotness varies from place to place. It is not necessarily the case that a material in a particular place is in a state that is steady and nearly homogeneous enough to allow it to have a well-defined hotness or temperature. Hotness may be represented abstractly as a one-dimensional manifold. Every valid temperature scale has its own one-to-one map into the hotness manifold.[39][40]
When two systems in thermal contact are at the same temperature no heat transfers between them. When a temperature difference does exist heat flows spontaneously from the warmer system to the colder system until they are in thermal equilibrium. Such heat transfer occurs by conduction or by thermal radiation.[41][42][43][44][45][46][47][48]
Experimental physicists, for example Galileo and Newton,[49] found that there are indefinitely many empirical temperature scales. Nevertheless, the zeroth law of thermodynamics says that they all measure the same quality. This means that for a body in its own state of internal thermodynamic equilibrium, every correctly calibrated thermometer, of whatever kind, that measures the temperature of the body, records one and the same temperature. For a body that is not in its own state of internal thermodynamic equilibrium, different thermometers can record different temperatures, depending respectively on the mechanisms of operation of the thermometers.
Bodies in thermodynamic equilibrium
For experimental physics, hotness means that, when comparing any two given bodies in their respective separate thermodynamic equilibria, any two suitably given empirical thermometers with numerical scale readings will agree as to which is the hotter of the two given bodies, or that they have the same temperature.[50] This does not require the two thermometers to have a linear relation between their numerical scale readings, but it does require that the relation between their numerical readings shall be strictly monotonic.[51][52] A definite sense of greater hotness can be had, independently of calorimetry, of thermodynamics, and of properties of particular materials, from Wien's displacement law of thermal radiation: the temperature of a bath of thermal radiation is proportional, by a universal constant, to the frequency of the maximum of its frequency spectrum; this frequency is always positive, but can have values that tend to zero. Thermal radiation is initially defined for a cavity in thermodynamic equilibrium. These physical facts justify a mathematical statement that hotness exists on an ordered one-dimensional manifold. This is a fundamental character of temperature and thermometers for bodies in their own thermodynamic equilibrium.[7][39][40][53][54]
Except for a system undergoing a first-order phase change such as the melting of ice, as a closed system receives heat, without change in its volume and without change in external force fields acting on it, its temperature rises. For a system undergoing such a phase change so slowly that departure from thermodynamic equilibrium can be neglected, its temperature remains constant as the system is supplied with latent heat. Conversely, a loss of heat from a closed system, without phase change, without change of volume, and without change in external force fields acting on it, decreases its temperature.[55]
Bodies in a steady state but not in thermodynamic equilibrium
While for bodies in their own thermodynamic equilibrium states, the notion of temperature requires that all empirical thermometers must agree as to which of two bodies is the hotter or that they are at the same temperature, this requirement is not safe for bodies that are in steady states though not in thermodynamic equilibrium. It can then well be that different empirical thermometers disagree about which is the hotter, and if this is so, then at least one of the bodies does not have a well defined absolute thermodynamic temperature. Nevertheless, any one given body and any one suitable empirical thermometer can still support notions of empirical, non-absolute, hotness and temperature, for a suitable range of processes. This is a matter for study in non-equilibrium thermodynamics.
Bodies not in a steady state
When a body is not in a steady state, then the notion of temperature becomes even less safe than for a body in a steady state not in thermodynamic equilibrium. This is also a matter for study in non-equilibrium thermodynamics.
Thermodynamic equilibrium axiomatics
For axiomatic treatment of thermodynamic equilibrium, since the 1930s, it has become customary to refer to a zeroth law of thermodynamics. The customarily stated minimalist version of such a law postulates only that all bodies, which when thermally connected would be in thermal equilibrium, should be said to have the same temperature by definition, but by itself does not establish temperature as a quantity expressed as a real number on a scale. A more physically informative version of such a law views empirical temperature as a chart on a hotness manifold.[39][54][56] While the zeroth law permits the definitions of many different empirical scales of temperature, the second law of thermodynamics selects the definition of a single preferred, absolute temperature, unique up to an arbitrary scale factor, whence called the thermodynamic temperature.[7][39][57][58][59][60] If internal energy is considered as a function of the volume and entropy of a homogeneous system in thermodynamic equilibrium, thermodynamic absolute temperature appears as the partial derivative of internal energy with respect the entropy at constant volume. Its natural, intrinsic origin or null point is absolute zero at which the entropy of any system is at a minimum. Although this is the lowest absolute temperature described by the model, the third law of thermodynamics postulates that absolute zero cannot be attained by any physical system.
Heat capacity
When an energy transfer to or from a body is only as heat, the state of the body changes. Depending on the surroundings and the walls separating them from the body, various changes are possible in the body. They include chemical reactions, increase of pressure, increase of temperature, and phase change. For each kind of change under specified conditions, the heat capacity is the ratio of the quantity of heat transferred to the magnitude of the change. For example, if the change is an increase in temperature at constant volume, with no phase change and no chemical change, then the temperature of the body rises and its pressure increases. The quantity of heat transferred, ΔQ, divided by the observed temperature change, ΔT, is the body's heat capacity at constant volume:
If heat capacity is measured for a well defined amount of substance, the specific heat is the measure of the heat required to increase the temperature of such a unit quantity by one unit of temperature. For example, to raise the temperature of water by one kelvin (equal to one degree Celsius) requires 4186 joules per kilogram (J/kg).
Measurement

Temperature measurement using modern scientific thermometers and temperature scales goes back at least as far as the early 18th century, when Gabriel Fahrenheit adapted a thermometer (switching to mercury) and a scale both developed by Ole Christensen Rømer. Fahrenheit's scale is still in use in the United States for non-scientific applications.
Temperature is measured with thermometers that may be calibrated to a variety of temperature scales. In most of the world (except for Belize, Myanmar, Liberia and the United States), the Celsius scale is used for most temperature measuring purposes. Most scientists measure temperature using the Celsius scale and thermodynamic temperature using the Kelvin scale, which is the Celsius scale offset so that its null point is 0 K = −273.15 °C, or absolute zero. Many engineering fields in the US, notably high-tech and US federal specifications (civil and military), also use the Kelvin and Celsius scales. Other engineering fields in the US also rely upon the Rankine scale (a shifted Fahrenheit scale) when working in thermodynamic-related disciplines such as combustion.
Units
The basic unit of temperature in the International System of Units (SI) is the Kelvin. It has the symbol K.
For everyday applications, it is often convenient to use the Celsius scale, in which 0 °C corresponds very closely to the freezing point of water and 100 °C is its boiling point at sea level. Because liquid droplets commonly exist in clouds at sub-zero temperatures, 0 °C is better defined as the melting point of ice. In this scale a temperature difference of 1 degree Celsius is the same as a 1kelvin increment, but the scale is offset by the temperature at which ice melts (273.15 K).
By international agreement,[61] until May 2019, the Kelvin and Celsius scales were defined by two fixing points: absolute zero and the triple point of Vienna Standard Mean Ocean Water, which is water specially prepared with a specified blend of hydrogen and oxygen isotopes. Absolute zero was defined as precisely 0 K and −273.15 °C. It is the temperature at which all classical translational motion of the particles comprising matter ceases and they are at complete rest in the classical model. Quantum-mechanically, however, zero-point motion remains and has an associated energy, the zero-point energy. Matter is in its ground state,[62] and contains no thermal energy. The triple point of water is defined as 273.16 K and 0.01 °C. This definition served the following purposes: it fixed the magnitude of the kelvin as being precisely 1 part in 273.16 parts of the difference between absolute zero and the triple point of water; it establishes that one kelvin has precisely the same magnitude as one degree on the Celsius scale; and it established the difference between the null points of these scales as being 273.15 K (0 K = −273.15 °C and 273.16 K = 0.01 °C). Since 2019, there has been a new definition based on the Boltzmann constant,[63] but the scales are scarcely changed.
In the United States, the Fahrenheit scale is widely used. On this scale the freezing point of water corresponds to 32 °F and the boiling point to 212 °F. The Rankine scale, still used in fields of chemical engineering in the US, is an absolute scale based on the Fahrenheit increment.
Conversion
The following table shows the temperature conversion formulas for conversions to and from the Celsius scale.
| from Celsius | to Celsius | |
|---|---|---|
| Fahrenheit | [°F] = [°C] × 9⁄5 + 32 | [°C] = ([°F] − 32) × 5⁄9 |
| Kelvin | [K] = [°C] + 273.15 | [°C] = [K] − 273.15 |
| Rankine | [°R] = ([°C] + 273.15) × 9⁄5 | [°C] = ([°R] − 491.67) × 5⁄9 |
| Delisle | [°De] = (100 − [°C]) × 3⁄2 | [°C] = 100 − [°De] × 2⁄3 |
| Newton | [°N] = [°C] × 33⁄100 | [°C] = [°N] × 100⁄33 |
| Réaumur | [°Ré] = [°C] × 4⁄5 | [°C] = [°Ré] × 5⁄4 |
| Rømer | [°Rø] = [°C] × 21⁄40 + 7.5 | [°C] = ([°Rø] − 7.5) × 40⁄21 |
Plasma physics
The field of plasma physics deals with phenomena of electromagnetic nature that involve very high temperatures. It is customary to express temperature as energy in units of electronvolts (eV) or kiloelectronvolts (keV). The energy, which has a different dimension from temperature, is then calculated as the product of the Boltzmann constant and temperature, . Then, 1 eV corresponds to 11605 K. In the study of QCD matter one routinely encounters temperatures of the order of a few hundred MeV, equivalent to about 1012 K.
Theoretical foundation
Historically, there are several scientific approaches to the explanation of temperature: the classical thermodynamic description based on macroscopic empirical variables that can be measured in a laboratory; the kinetic theory of gases which relates the macroscopic description to the probability distribution of the energy of motion of gas particles; and a microscopic explanation based on statistical physics and quantum mechanics. In addition, rigorous and purely mathematical treatments have provided an axiomatic approach to classical thermodynamics and temperature.[64] Statistical physics provides a deeper understanding by describing the atomic behavior of matter, and derives macroscopic properties from statistical averages of microscopic states, including both classical and quantum states. In the fundamental physical description, using natural units, temperature may be measured directly in units of energy. However, in the practical systems of measurement for science, technology, and commerce, such as the modern metric system of units, the macroscopic and the microscopic descriptions are interrelated by the Boltzmann constant, a proportionality factor that scales temperature to the microscopic mean kinetic energy.
The microscopic description in statistical mechanics is based on a model that analyzes a system into its fundamental particles of matter or into a set of classical or quantum-mechanical oscillators and considers the system as a statistical ensemble of microstates. As a collection of classical material particles, temperature is a measure of the mean energy of motion, called kinetic energy, of the particles, whether in solids, liquids, gases, or plasmas. The kinetic energy, a concept of classical mechanics, is half the mass of a particle times its speed squared. In this mechanical interpretation of thermal motion, the kinetic energies of material particles may reside in the velocity of the particles of their translational or vibrational motion or in the inertia of their rotational modes. In monatomic perfect gases and, approximately, in most gases, temperature is a measure of the mean particle kinetic energy. It also determines the probability distribution function of the energy. In condensed matter, and particularly in solids, this purely mechanical description is often less useful and the oscillator model provides a better description to account for quantum mechanical phenomena. Temperature determines the statistical occupation of the microstates of the ensemble. The microscopic definition of temperature is only meaningful in the thermodynamic limit, meaning for large ensembles of states or particles, to fulfill the requirements of the statistical model.
The kinetic energy is also considered as a component of thermal energy. The thermal energy may be partitioned into independent components attributed to the degrees of freedom of the particles or to the modes of oscillators in a thermodynamic system. In general, the number of these degrees of freedom that are available for the equipartitioning of energy depends on the temperature, i.e. the energy region of the interactions under consideration. For solids, the thermal energy is associated primarily with the vibrations of its atoms or molecules about their equilibrium position. In an ideal monatomic gas, the kinetic energy is found exclusively in the purely translational motions of the particles. In other systems, vibrational and rotational motions also contribute degrees of freedom.
Kinetic theory of gases
Maxwell and Boltzmann developed a kinetic theory that yields a fundamental understanding of temperature in gases.[65] This theory also explains the ideal gas law and the observed heat capacity of monatomic (or 'noble') gases.[66][67][68]
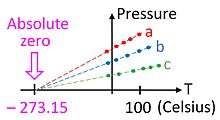
The ideal gas law is based on observed empirical relationships between pressure (p), volume (V), and temperature (T), and was recognized long before the kinetic theory of gases was developed (see Boyle's and Charles's laws). The ideal gas law states:[69]
where n is the number of moles of gas and R = 8.314462618... J⋅mol−1⋅K−1[70] is the gas constant.
This relationship gives us our first hint that there is an absolute zero on the temperature scale, because it only holds if the temperature is measured on an absolute scale such as Kelvin's. The ideal gas law allows one to measure temperature on this absolute scale using the gas thermometer. The temperature in kelvins can be defined as the pressure in pascals of one mole of gas in a container of one cubic meter, divided by the gas constant.
Although it is not a particularly convenient device, the gas thermometer provides an essential theoretical basis by which all thermometers can be calibrated. As a practical matter, it is not possible to use a gas thermometer to measure absolute zero temperature since the gases tend to condense into a liquid long before the temperature reaches zero. It is possible, however, to extrapolate to absolute zero by using the ideal gas law, as shown in the figure.
The kinetic theory assumes that pressure is caused by the force associated with individual atoms striking the walls, and that all energy is translational kinetic energy. Using a sophisticated symmetry argument,[71] Boltzmann deduced what is now called the Maxwell–Boltzmann probability distribution function for the velocity of particles in an ideal gas. From that probability distribution function, the average kinetic energy (per particle) of a monatomic ideal gas is[67][72]
where the Boltzmann constant kB is the ideal gas constant divided by the Avogadro number, and is the root-mean-square speed. Thus the ideal gas law states that internal energy is directly proportional to temperature.[73] This direct proportionality between temperature and internal energy is a special case of the equipartition theorem, and holds only in the classical limit of an ideal gas. It does not hold for most substances, although it is true that temperature is a monotonic (non-decreasing) function of internal energy.
Zeroth law of thermodynamics
When two otherwise isolated bodies are connected together by a rigid physical path impermeable to matter, there is spontaneous transfer of energy as heat from the hotter to the colder of them. Eventually, they reach a state of mutual thermal equilibrium, in which heat transfer has ceased, and the bodies' respective state variables have settled to become unchanging.
One statement of the zeroth law of thermodynamics is that if two systems are each in thermal equilibrium with a third system, then they are also in thermal equilibrium with each other.
This statement helps to define temperature but it does not, by itself, complete the definition. An empirical temperature is a numerical scale for the hotness of a thermodynamic system. Such hotness may be defined as existing on a one-dimensional manifold, stretching between hot and cold. Sometimes the zeroth law is stated to include the existence of a unique universal hotness manifold, and of numerical scales on it, so as to provide a complete definition of empirical temperature.[56] To be suitable for empirical thermometry, a material must have a monotonic relation between hotness and some easily measured state variable, such as pressure or volume, when all other relevant coordinates are fixed. An exceptionally suitable system is the ideal gas, which can provide a temperature scale that matches the absolute Kelvin scale. The Kelvin scale is defined on the basis of the second law of thermodynamics.
Second law of thermodynamics
As an alternative to considering or defining the zeroth law of thermodynamics, it was the historical development in thermodynamics to define temperature in terms of the second law of thermodynamics which deals with entropy. The second law states that any process will result in either no change or a net increase in the entropy of the universe. This can be understood in terms of probability.
For example, in a series of coin tosses, a perfectly ordered system would be one in which either every toss comes up heads or every toss comes up tails. This means the outcome is always 100% the same result. In contrast, many mixed (disordered) outcomes are possible, and their number increases with each toss. Eventually, the combinations of ~50% heads and ~50% tails dominate and obtaining an outcome significantly different from 50/50 becomes increasingly unlikely. Thus the system naturally progresses to a state of maximum disorder or entropy.
As temperature governs the transfer of heat between two systems and the universe tends to progress toward a maximum of entropy, it is expected that there is some relationship between temperature and entropy. A heat engine is a device for converting thermal energy into mechanical energy, resulting in the performance of work. and analysis of the Carnot heat engine provides the necessary relationships. The work from a heat engine corresponds to the difference between the heat put into the system at high temperature, qH and the heat extracted at the low temperature, qC. The efficiency is the work divided by the heat input:
-
(4)
where wcy is the work done per cycle. The efficiency depends only on qC/qH. Because qC and qH correspond to heat transfer at the temperatures TC and TH respectively, qC/qH should be some function of these temperatures:
-
(5)
Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient. Thus, a heat engine operating between T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and T2, and the second between T2 and T3. This can only be the case if
which implies
Since the first function is independent of T2, this temperature must cancel on the right side, meaning f(T1, T3) is of the form g(T1)/g(T3) (i.e. f(T1, T3) = f(T1, T2)f(T2, T3) = g(T1)/g(T2) · g(T2)/g(T3) = g(T1)/g(T3)), where g is a function of a single temperature. A temperature scale can now be chosen with the property that
-
(6)
Substituting (6) back into (4) gives a relationship for the efficiency in terms of temperature:
-
(7)
For TC = 0 K the efficiency is 100% and that efficiency becomes greater than 100% below 0 K. Since an efficiency greater than 100% violates the first law of thermodynamics, this implies that 0 K is the minimum possible temperature. In fact the lowest temperature ever obtained in a macroscopic system was 20 nK, which was achieved in 1995 at NIST. Subtracting the right hand side of (5) from the middle portion and rearranging gives
where the negative sign indicates heat ejected from the system. This relationship suggests the existence of a state function, S, defined by
-
(8)
where the subscript indicates a reversible process. The change of this state function around any cycle is zero, as is necessary for any state function. This function corresponds to the entropy of the system, which was described previously. Rearranging (8) gives a formula for temperature in terms of fictive infinitesimal quasi-reversible elements of entropy and heat:
-
(9)
For a system, where entropy S(E) is a function of its energy E, the temperature T is given by
-
(10)
i.e. the reciprocal of the temperature is the rate of increase of entropy with respect to energy.
Definition from statistical mechanics
Statistical mechanics defines temperature based on a system's fundamental degrees of freedom. Eq.(10) is the defining relation of temperature. Eq. (9) can be derived from the principles underlying the fundamental thermodynamic relation.
Generalized temperature from single-particle statistics
It is possible to extend the definition of temperature even to systems of few particles, like in a quantum dot. The generalized temperature is obtained by considering time ensembles instead of configuration-space ensembles given in statistical mechanics in the case of thermal and particle exchange between a small system of fermions (N even less than 10) with a single/double-occupancy system. The finite quantum grand canonical ensemble,[74] obtained under the hypothesis of ergodicity and orthodicity,[75] allows expressing the generalized temperature from the ratio of the average time of occupation and of the single/double-occupancy system:[76]
where EF is the Fermi energy. This generalized temperature tends to the ordinary temperature when N goes to infinity.
Negative temperature
On the empirical temperature scales that are not referenced to absolute zero, a negative temperature is one below the zero-point of the scale used. For example, dry ice has a sublimation temperature of −78.5 °C which is equivalent to −109.3 °F. On the absolute kelvin scale this temperature is 194.6 K. No body can be brought to exactly 0 K (the temperature of the ideally coldest possible body) by any finite practicable process; this is a consequence of the third law of thermodynamics.
The international kinetic theory temperature of a body cannot take negative values. The thermodynamic temperature scale, however, is not so constrained.
For a body of matter, there can sometimes be conceptually defined, in terms of microscopic degrees of freedom, namely particle spins, a subsystem, with a temperature other than that of the whole body. When the body is in its own state of internal thermodynamic equilibrium, the temperatures of the whole body and of the subsystem must be the same. The two temperatures can differ when, by work through externally imposed force fields, energy can be transferred to and from the subsystem, separately from the rest of the body; then the whole body is not in its own state of internal thermodynamic equilibrium. There is an upper limit of energy such a spin subsystem can attain.
Considering the subsystem to be in a temporary state of virtual thermodynamic equilibrium, it is possible to obtain a negative temperature on the thermodynamic scale. Thermodynamic temperature is the inverse of the derivative of the subsystem's entropy with respect to its internal energy. As the subsystem's internal energy increases, the entropy increases for some range, but eventually attains a maximum value and then begins to decrease as the highest energy states begin to fill. At the point of maximum entropy, the temperature function shows the behavior of a singularity, because the slope of the entropy function decreases to zero and then turns negative. As the subsystem's entropy reaches its maximum, its thermodynamic temperature goes to positive infinity, switching to negative infinity as the slope turns negative. Such negative temperatures are hotter than any positive temperature. Over time, when the subsystem is exposed to the rest of the body, which has a positive temperature, energy is transferred as heat from the negative temperature subsystem to the positive temperature system.[77] The kinetic theory temperature is not defined for such subsystems.
Examples
| Temperature | Peak emittance wavelength[78] of black-body radiation | ||
|---|---|---|---|
| Kelvin | Celsius | ||
| Absolute zero (precisely by definition) |
0 K | −273.15 °C | Cannot be defined |
| Blackbody temperature of Sagittarius A*, the black hole at the centre of our galaxy[79] |
17 fK | −273.149999999999983 °C | 1.7×108 km (1.1 AU) |
| Lowest temperature achieved[80] |
100 pK | −273.149999999900 °C | 29000 km |
| Coldest Bose–Einstein condensate[81] |
450 pK | −273.14999999955 °C | 6400 km |
| One millikelvin (precisely by definition) |
0.001 K | −273.149 °C | 2.89777 m (radio, FM band)[82] |
| Cosmic microwave background (2013 measurement) |
2.7260 K | −270.424 °C | 0.00106301 m (millimeter-wavelength microwave) |
| Water triple point (precisely by definition) |
273.16 K | 0.01 °C | 10608.3 nm (long-wavelength IR) |
| Water boiling point[A] | 373.1339 K | 99.9839 °C | 7766.03 nm (mid-wavelength IR) |
| Iron melting point | 1811 K | 1538 °C | 1600 nm (far infrared) |
| Incandescent lamp[B] | 2500 K | ≈2200 °C | 1160 nm (near infrared)[C] |
| Sun's visible surface[D][83] | 5778 K | 5505 °C | 501.5 nm (green-blue light) |
| Lightning bolt channel[E] |
28 kK | 28000 °C | 100 nm (far ultraviolet light) |
| Sun's core[E] | 16 MK | 16 million °C | 0.18 nm (X-rays) |
| Thermonuclear weapon (peak temperature)[E][84] |
350 MK | 350 million °C | 8.3×10−3 nm (gamma rays) |
| Sandia National Labs' Z machine[E][85] |
2 GK | 2 billion °C | 1.4×10−3 nm (gamma rays)[F] |
| Core of a high-mass star on its last day[E][86] |
3 GK | 3 billion °C | 1×10−3 nm (gamma rays) |
| Merging binary neutron star system[E][87] |
350 GK | 350 billion °C | 8×10−6 nm (gamma rays) |
| Relativistic Heavy Ion Collider[E][88] |
1 TK | 1 trillion °C | 3×10−6 nm (gamma rays) |
| CERN's proton vs nucleus collisions[E][89] |
10 TK | 10 trillion °C | 3×10−7 nm (gamma rays) |
| Universe 5.391×10−44 s after the Big Bang[E] |
1.417×1032 K (Planck temperature) |
1.417×1032 °C | 1.616×10−27 nm (Planck length)[90] |
- A For Vienna Standard Mean Ocean Water at one standard atmosphere (101.325 kPa) when calibrated strictly per the two-point definition of thermodynamic temperature.
- B The 2500 K value is approximate. The 273.15 K difference between K and °C is rounded to 300 K to avoid false precision in the Celsius value.
- C For a true black-body (which tungsten filaments are not). Tungsten filament emissivity is greater at shorter wavelengths, which makes them appear whiter.
- D Effective photosphere temperature. The 273.15 K difference between K and °C is rounded to 273 K to avoid false precision in the Celsius value.
- E The 273.15 K difference between K and °C is within the precision of these values.
- F For a true black-body (which the plasma was not). The Z machine's dominant emission originated from 40 MK electrons (soft x-ray emissions) within the plasma.
See also
- Atmospheric temperature
- Body temperature – Ability of an organism to keep its body temperature within certain boundaries (thermoregulation)
- Color temperature – property of light sources related to black-body radiation
- Dry-bulb temperature
- Thermal conduction
- Convective heat transfer
- Instrumental temperature record – In situ measurements that provides the temperature of Earth's climate system
- ISO 1
- International Temperature Scale of 1990 (ITS-90)
- Laser schlieren deflectometry
- List of cities by average temperature – Wikimedia list article
- Maxwell's demon – Thought experiment
- Orders of magnitude (temperature) – Range of temperatures from absolute zero to very high
- Outside air temperature
- Planck temperature
- Rankine scale – Absolute temperature scale using Fahrenheit degrees
- Relativistic heat conduction – The modelling of heat conduction and similar diffusion processes in a way compatible with special relativity.
- Satellite temperature measurements
- Scale of temperature
- Sea surface temperature – Water temperature close to the ocean's surface
- Stagnation temperature
- Thermal radiation
- Thermoception
- Thermodynamic (absolute) temperature – Absolute measure of temperature
- Thermography
- Thermometer – Device to measure temperature
- Virtual temperature
- Wet-bulb globe temperature
- Wet-bulb temperature – Temperature read by a thermometer covered in water-soaked cloth
Notes and references
- Agency, International Atomic Energy (1974). Thermal discharges at nuclear power stations: their management and environmental impacts : a report prepared by a group of experts as the result of a panel meeting held in Vienna, 23–27 October 1972. International Atomic Energy Agency.
- Watkinson, John (2001). The Art of Digital Audio. Taylor & Francis. ISBN 978-0-240-51587-8.
- Middleton, W.E.K. (1966), pp. 89–105.
- Jaynes, E.T. (1965), pp. 391–398.
- Cryogenic Society (2019).
- Draft Resolution A "On the revision of the International System of units (SI)" to be submitted to the CGPM at its 26th meeting (2018) (PDF)
- Truesdell, C.A. (1980), Sections 11 B, 11H, pp. 306–310, 320–332.
- Quinn, T. J. (1983).
- Germer, L.H. (1925). 'The distribution of initial velocities among thermionic electrons', Phys. Rev., 25: 795–807. here
- Turvey, K. (1990). 'Test of validity of Maxwellian statistics for electrons thermionically emitted from an oxide cathode', European Journal of Physics, 11(1): 51–59. here
- Zeppenfeld, M., Englert, B.G.U., Glöckner, R., Prehn, A., Mielenz, M., Sommer, C., van Buuren, L.D., Motsch, M., Rempe, G. (2012).
- Miller, J. (2013).
- de Podesta, M., Underwood, R., Sutton, G., Morantz, P, Harris, P, Mark, D.F., Stuart, F.M., Vargha, G., Machin, M. (2013). A low-uncertainty measurement of the Boltzmann constant, Metrologia, 50 (4): S213–S216, BIPM & IOP Publishing Ltd
- Quinn, T.J. (1983), pp. 98–107.
- Schooley, J.F. (1986), pp. 138–143.
- Quinn, T.J. (1983), pp. 61–83.
- Schooley, J.F. (1986), pp. 115–138.
- Adkins, C.J. (1968/1983), pp. 119–120.
- Buchdahl, H.A. (1966), pp. 137–138.
- Tschoegl, N.W. (2000), p. 88.
- Thomson, W. (Lord Kelvin) (1848).
- Thomson, W. (Lord Kelvin) (1851).
- Partington, J.R. (1949), pp. 175–177.
- Roberts, J.K., Miller, A.R. (1928/1960), pp. 321–322.
- Quinn, T.J. (1983). Temperature, Academic Press, London, ISBN 0-12-569680-9, pp. 160–162.
- Tisza, L. (1966). Generalized Thermodynamics, M.I.T. Press, Cambridge MA, pp. 47, 57.
- Münster, A. (1970), Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London, ISBN 0-471-62430-6, pp. 49, 69.
- Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 14–15, 214.
- Callen, H.B. (1960/1985), Thermodynamics and an Introduction to Thermostatistics, (first edition 1960), second edition 1985, John Wiley & Sons, New York, ISBN 0-471-86256-8, pp. 146–148.
- Kondepudi, D., Prigogine, I. (1998). Modern Thermodynamics. From Heat Engines to Dissipative Structures, John Wiley, Chichester, ISBN 0-471-97394-7, pp. 115–116.
- Tisza, L. (1966). Generalized Thermodynamics, M.I.T. Press, Cambridge MA, p. 58.
- Milne, E.A. (1929). The effect of collisions on monochromatic radiative equilibrium, Monthly Notices of the Royal Astronomical Society, 88: 493–502.
- Gyarmati, I. (1970). Non-equilibrium Thermodynamics. Field Theory and Variational Principles, translated by E. Gyarmati and W.F. Heinz, Springer, Berlin, pp. 63–66.
- Glansdorff, P., Prigogine, I., (1971). Thermodynamic Theory of Structure, Stability and Fluctuations, Wiley, London, ISBN 0-471-30280-5, pp. 14–16.
- Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 133–135.
- Callen, H.B. (1960/1985), Thermodynamics and an Introduction to Thermostatistics, (first edition 1960), second edition 1985, John Wiley & Sons, New York, ISBN 0-471-86256-8, pp. 309–310.
- Bryan, G.H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications, B.G. Teubner, Leipzig, p. 3. "Thermodynamics by George Hartley Bryan". Archived from the original on 2011-11-18. Retrieved 2011-10-02.
- Pippard, A.B. (1957/1966), p. 18.
- Mach, E. (1900). Die Principien der Wärmelehre. Historisch-kritisch entwickelt, Johann Ambrosius Barth, Leipzig, section 22, pp. 56–57.
- Serrin, J. (1986). Chapter 1, 'An Outline of Thermodynamical Structure', pp. 3–32, especially p. 6, in New Perspectives in Thermodynamics, edited by J. Serrin, Springer, Berlin, ISBN 3-540-15931-2.
- Maxwell, J.C. (1872). Theory of Heat, third edition, Longmans, Green, London, p. 32.
- Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, pp. 39–40.
- Planck, M. (1897/1903). Treatise on Thermodynamics, translated by A. Ogg, Longmans, Green, London, pp. 1–2.
- Planck, M. (1914), The Theory of Heat Radiation Archived 2011-11-18 at the Wayback Machine, second edition, translated into English by M. Masius, Blakiston's Son & Co., Philadelphia, reprinted by Kessinger.
- J.S. Dugdale (1996). Entropy and its Physical Interpretation. Taylor & Francis. p. 13. ISBN 978-0-7484-0569-5.
- F. Reif (1965). Fundamentals of Statistical and Thermal Physics. McGraw-Hill. p. 102.
- M.J. Moran; H.N. Shapiro (2006). "1.6.1". Fundamentals of Engineering Thermodynamics (5 ed.). John Wiley & Sons, Ltd. p. 14. ISBN 978-0-470-03037-0.
- T.W. Leland, Jr. "Basic Principles of Classical and Statistical Thermodynamics" (PDF). p. 14. Archived (PDF) from the original on 2011-09-28.
Consequently we identify temperature as a driving force which causes something called heat to be transferred.
- Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, pp. 42, 103–117.
- Beattie, J.A., Oppenheim, I. (1979). Principles of Thermodynamics, Elsevier Scientific Publishing Company, Amsterdam, ISBN 978-0-444-41806-7, p. 29.
- Landsberg, P.T. (1961). Thermodynamics with Quantum Statistical Illustrations, Interscience Publishers, New York, p. 17.
- Thomsen, J.S. (1962). "A restatement of the zeroth law of thermodynamics". Am. J. Phys. 30 (4): 294–296. Bibcode:1962AmJPh..30..294T. doi:10.1119/1.1941991.
- Maxwell, J.C. (1872). Theory of Heat, third edition, Longman's, Green & Co, London, p. 45.
- Pitteri, M. (1984). On the axiomatic foundations of temperature, Appendix G6 on pp. 522–544 of Rational Thermodynamics, C. Truesdell, second edition, Springer, New York, ISBN 0-387-90874-9.
- Truesdell, C., Bharatha, S. (1977). The Concepts and Logic of Classical Thermodynamics as a Theory of Heat Engines, Rigorously Constructed upon the Foundation Laid by S. Carnot and F. Reech, Springer, New York, ISBN 0-387-07971-8, p. 20.
- Serrin, J. (1978). The concepts of thermodynamics, in Contemporary Developments in Continuum Mechanics and Partial Differential Equations. Proceedings of the International Symposium on Continuum Mechanics and Partial Differential Equations, Rio de Janeiro, August 1977, edited by G.M. de La Penha, L.A.J. Medeiros, North-Holland, Amsterdam, ISBN 0-444-85166-6, pp. 411–451.
- Maxwell, J.C. (1872). Theory of Heat, third edition, Longmans, Green, London, pp. 155–158.
- Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, Section 95, pp. 68–69.
- Buchdahl, H.A. (1966), p. 73.
- Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8, Section 32., pp. 106–108.
- The kelvin in the SI Brochure Archived 2007-09-26 at the Wayback Machine
- "Absolute Zero". Calphad.com. Archived from the original on 2011-07-08. Retrieved 2010-09-16.
- Definition agreed by the 26th General Conference on Weights and Measures (CGPM) in November 2018, implemented 20 May 2019
- C. Caratheodory (1909). "Untersuchungen über die Grundlagen der Thermodynamik". Mathematische Annalen. 67 (3): 355–386. doi:10.1007/BF01450409.
- Swendsen, Robert (March 2006). "Statistical mechanics of colloids and Boltzmann's definition of entropy" (PDF). American Journal of Physics. 74 (3): 187–190. Bibcode:2006AmJPh..74..187S. doi:10.1119/1.2174962.
- Balescu, R. (1975). Equilibrium and Nonequilibrium Statistical Mechanics, Wiley, New York, ISBN 0-471-04600-0, pp. 148–154.
- Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (2nd ed.). W.H. Freeman Company. pp. 391–397. ISBN 978-0-7167-1088-2.
- Kondepudi, D.K. (1987). "Microscopic aspects implied by the second law". Foundations of Physics. 17 (7): 713–722. Bibcode:1987FoPh...17..713K. doi:10.1007/BF01889544.
- Feynman, R.P., Leighton, R.B., Sands, M. (1963). The Feynman Lectures on Physics, Addison–Wesley, Reading MA, volume 1, pp. 39-6 to 39-12.
- "2018 CODATA Value: molar gas constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- "Kinetic Theory". galileo.phys.virginia.edu. Archived from the original on 16 July 2017. Retrieved 27 January 2018.
- Tolman, R.C. (1938). The Principles of Statistical Mechanics, Oxford University Press, London, pp. 93, 655.
- Peter Atkins, Julio de Paula (2006). Physical Chemistry (8 ed.). Oxford University Press. p. 9.
- Prati, E. (2010). "The finite quantum grand canonical ensemble and temperature from single-electron statistics for a mesoscopic device". J. Stat. Mech. 1 (1): P01003. arXiv:1001.2342. Bibcode:2010JSMTE..01..003P. doi:10.1088/1742-5468/2010/01/P01003. arxiv.org Archived 2017-11-22 at the Wayback Machine
- "Archived copy" (PDF). Archived (PDF) from the original on 2014-04-13. Retrieved 2014-04-11.CS1 maint: archived copy as title (link)
- Prati, E.; et al. (2010). "Measuring the temperature of a mesoscopic electron system by means of single electron statistics". Applied Physics Letters. 96 (11): 113109. arXiv:1002.0037. Bibcode:2010ApPhL..96k3109P. doi:10.1063/1.3365204. Archived from the original on 2016-05-14. arxiv.org Archived 2017-11-22 at the Wayback Machine
- Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (2nd ed.). W.H. Freeman Company. p. Appendix E. ISBN 978-0-7167-1088-2.
- The cited emission wavelengths are for black bodies in equilibrium. CODATA 2006 recommended value of 2.8977685(51)×10−3 m K used for Wien displacement law constant b.
- This the Hawking Radiation for a Schwarzschild black hole of mass M = 3.6×106 M☉. It is too faint to be observed. The mass estimate is from Schödel, R.; Merritt, D.; Eckart, A. (July 2009). "The nuclear star cluster of the Milky Way: Proper motions and mass". Astronomy and Astrophysics. 502 (1): 91–111. arXiv:0902.3892. Bibcode:2009A&A...502...91S. doi:10.1051/0004-6361/200810922.
- "World record in low temperatures". Archived from the original on 2009-06-18. Retrieved 2009-05-05.
- A temperature of 450 ±80 pK in a Bose–Einstein condensate (BEC) of sodium atoms was achieved in 2003 by researchers at MIT. Citation: Cooling Bose–Einstein Condensates Below 500 Picokelvin, A.E. Leanhardt et al., Science 301, 12 Sept. 2003, p. 1515. It's noteworthy that this record's peak emittance black-body wavelength of 6,400 kilometers is roughly the radius of Earth.
- The peak emittance wavelength of 2.89777 m is a frequency of 103.456 MHz
- Measurement was made in 2002 and has an uncertainty of ±3 kelvins. A 1989 measurement Archived 2010-02-11 at the Wayback Machine produced a value of 5,777.0±2.5 K. Citation: Overview of the Sun (Chapter 1 lecture notes on Solar Physics by Division of Theoretical Physics, Dept. of Physical Sciences, University of Helsinki).
- The 350 MK value is the maximum peak fusion fuel temperature in a thermonuclear weapon of the Teller–Ulam configuration (commonly known as a hydrogen bomb). Peak temperatures in Gadget-style fission bomb cores (commonly known as an atomic bomb) are in the range of 50 to 100 MK. Citation: Nuclear Weapons Frequently Asked Questions, 3.2.5 Matter At High Temperatures. Link to relevant Web page. Archived 2007-05-03 at the Wayback Machine All referenced data was compiled from publicly available sources.
- Peak temperature for a bulk quantity of matter was achieved by a pulsed-power machine used in fusion physics experiments. The term bulk quantity draws a distinction from collisions in particle accelerators wherein high temperature applies only to the debris from two subatomic particles or nuclei at any given instant. The >2 GK temperature was achieved over a period of about ten nanoseconds during shot Z1137. In fact, the iron and manganese ions in the plasma averaged 3.58±0.41 GK (309±35 keV) for 3 ns (ns 112 through 115). Ion Viscous Heating in a Magnetohydrodynamically Unstable Z Pinch at Over 2×109 Kelvin, M.G. Haines et al., Physical Review Letters 96 (2006) 075003. Link to Sandia's news release. Archived 2010-05-30 at the Wayback Machine
- Core temperature of a high–mass (>8–11 solar masses) star after it leaves the main sequence on the Hertzsprung–Russell diagram and begins the alpha process (which lasts one day) of fusing silicon–28 into heavier elements in the following steps: sulfur–32 → argon–36 → calcium–40 → titanium–44 → chromium–48 → iron–52 → nickel–56. Within minutes of finishing the sequence, the star explodes as a Type II supernova. Citation: Stellar Evolution: The Life and Death of Our Luminous Neighbors (by Arthur Holland and Mark Williams of the University of Michigan). Link to Web site Archived 2009-01-16 at the Wayback Machine. More informative links can be found here "Archived copy". Archived from the original on 2013-04-11. Retrieved 2016-02-08.CS1 maint: archived copy as title (link), and here "Archived copy". Archived from the original on 2011-08-14. Retrieved 2016-02-08.CS1 maint: archived copy as title (link), and a concise treatise on stars by NASA is here "Archived copy". Archived from the original on 2010-10-24. Retrieved 2010-10-12.CS1 maint: archived copy as title (link). "Stellar". Archived from the original on January 16, 2009. Retrieved 2010-10-12.CS1 maint: BOT: original-url status unknown (link)
- Based on a computer model that predicted a peak internal temperature of 30 MeV (350 GK) during the merger of a binary neutron star system (which produces a gamma–ray burst). The neutron stars in the model were 1.2 and 1.6 solar masses respectively, were roughly 20 km in diameter, and were orbiting around their barycenter (common center of mass) at about 390 Hz during the last several milliseconds before they completely merged. The 350 GK portion was a small volume located at the pair's developing common core and varied from roughly 1 to 7 km across over a time span of around 5 ms. Imagine two city-sized objects of unimaginable density orbiting each other at the same frequency as the G4 musical note (the 28th white key on a piano). It's also noteworthy that at 350 GK, the average neutron has a vibrational speed of 30% the speed of light and a relativistic mass (m) 5% greater than its rest mass (m0). Torus Formation in Neutron Star Mergers and Well-Localized Short Gamma-Ray Bursts Archived 2017-11-22 at the Wayback Machine, R. Oechslin et al. of Max Planck Institute for Astrophysics. Archived 2005-04-03 at the Wayback Machine, arXiv:astro-ph/0507099 v2, 22 Feb. 2006. An html summary Archived 2010-11-09 at the Wayback Machine.
- Results of research by Stefan Bathe using the PHENIX Archived 2008-11-20 at the Wayback Machine detector on the Relativistic Heavy Ion Collider Archived 2016-03-03 at the Wayback Machine at Brookhaven National Laboratory Archived 2012-06-24 at the Wayback Machine in Upton, New York. Bathe has studied gold-gold, deuteron-gold, and proton-proton collisions to test the theory of quantum chromodynamics, the theory of the strong force that holds atomic nuclei together. Link to news release. Archived 2009-02-11 at the Wayback Machine
- How do physicists study particles? Archived 2007-10-11 at the Wayback Machine by CERN Archived 2012-07-07 at the Wayback Machine.
- The Planck frequency equals 1.85487(14)×1043 Hz (which is the reciprocal of one Planck time). Photons at the Planck frequency have a wavelength of one Planck length. The Planck temperature of 1.41679(11)×1032 K equates to a calculated b /T = λmax wavelength of 2.04531(16)×10−26 nm. However, the actual peak emittance wavelength quantizes to the Planck length of 1.61624(12)×10−26 nm.
Bibliography of cited references
- Adkins, C.J. (1968/1983). Equilibrium Thermodynamics, (1st edition 1968), third edition 1983, Cambridge University Press, Cambridge UK, ISBN 0-521-25445-0.
- Buchdahl, H.A. (1966). The Concepts of Classical Thermodynamics, Cambridge University Press, Cambridge.
- Jaynes, E.T. (1965). Gibbs vs Boltzmann entropies, American Journal of Physics, 33(5), 391–398.
- Middleton, W.E.K. (1966). A History of the Thermometer and its Use in Metrology, Johns Hopkins Press, Baltimore.
- Miller, J (2013). "Cooling molecules the optoelectric way". Physics Today. 66 (1): 12–14. Bibcode:2013PhT....66a..12M. doi:10.1063/pt.3.1840. Archived from the original on 2016-05-15.
- Partington, J.R. (1949). An Advanced Treatise on Physical Chemistry, volume 1, Fundamental Principles. The Properties of Gases, Longmans, Green & Co., London, pp. 175–177.
- Pippard, A.B. (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics, original publication 1957, reprint 1966, Cambridge University Press, Cambridge UK.
- Quinn, T.J. (1983). Temperature, Academic Press, London, ISBN 0-12-569680-9.
- Schooley, J.F. (1986). Thermometry, CRC Press, Boca Raton, ISBN 0-8493-5833-7.
- Roberts, J.K., Miller, A.R. (1928/1960). Heat and Thermodynamics, (first edition 1928), fifth edition, Blackie & Son Limited, Glasgow.
- Thomson, W. (Lord Kelvin) (1848). On an absolute thermometric scale founded on Carnot's theory of the motive power of heat, and calculated from Regnault's observations, Proc. Camb. Phil. Soc. (1843/1863) 1, No. 5: 66–71.
- Thomson, W. (Lord Kelvin) (March 1851). "On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule's equivalent of a Thermal Unit, and M. Regnault's Observations on Steam". Transactions of the Royal Society of Edinburgh. XX (part II): 261–268, 289–298.
- Truesdell, C.A. (1980). The Tragicomical History of Thermodynamics, 1822–1854, Springer, New York, ISBN 0-387-90403-4.
- Tschoegl, N.W. (2000). Fundamentals of Equilibrium and Steady-State Thermodynamics, Elsevier, Amsterdam, ISBN 0-444-50426-5.
- Zeppenfeld, M.; Englert, B.G.U.; Glöckner, R.; Prehn, A.; Mielenz, M.; Sommer, C.; van Buuren, L.D.; Motsch, M.; Rempe, G. (2012). "Sysiphus cooling of electrically trapped polyatomic molecules". Nature. 491 (7425): 570–573. arXiv:1208.0046. Bibcode:2012Natur.491..570Z. doi:10.1038/nature11595. PMID 23151480.
Further reading
- Chang, Hasok (2004). Inventing Temperature: Measurement and Scientific Progress. Oxford: Oxford University Press. ISBN 978-0-19-517127-3.
- Zemansky, Mark Waldo (1964). Temperatures Very Low and Very High. Princeton, NJ: Van Nostrand.