Generalized chi-squared distribution
In probability theory and statistics, the generalized chi-squared distribution (also generalized chi-square distribution) is the distribution of a linear sum of independent non-central chi-squared variables, or of a quadratic form of a multivariate normal distribution. It is a generalization of the chi-squared distribution. There are several other such generalizations for which the same term is sometimes used. Some of them are special cases of the family discussed here, for example the noncentral chi-squared distribution and the gamma distribution.
|
Probability density function 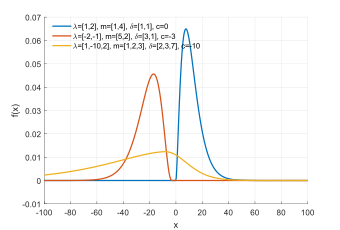 | |||
|
Cumulative distribution function 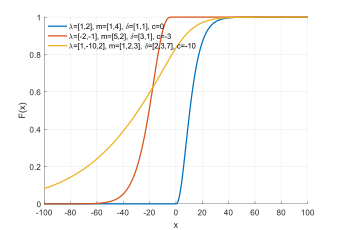 | |||
| Parameters |
, vector of weights of chi-square components , vector of degrees of freedom of chi-square components , vector of non-centrality parameters of chi-square components , constant term | ||
|---|---|---|---|
| Support | |||
| Mean | |||
| Variance | |||
Definition
There are multiple ways of formulating, and thus parameterizing, the generalized chi-squared variable. One is to write it as a linear sum of independent noncentral chi-squared variables [1][2]:
- .
Here the parameters are the coefficients , the degrees of freedom and noncentrality parameters of the constituent chi-squares, and a constant offset . Some important special cases of this have all coefficients the same sign, omit the constant term or have central chi-squared components.
Another is to formulate it as a quadratic form of a normal vector [3]:
- .
Here is a matrix, is a vector, and is a scalar. These, together with the mean and variance-covariance matrix of the normal vector , parameterize the distribution. If (and only if) in this formulation is positive-definite, all the in the other formulation will have the same sign.
One formulation of the generalized chi-squared distribution is as follows. Let z have a multivariate normal distribution with zero mean and covariance matrix B, then the value of the quadratic form X = zTAz, where A is a matrix, has a generalised chi-squared distribution with parameters A and B. Note that there is some redundancy in this formulation, as for any matrix C, the distribution with parameters CTAC and B is identical to the distribution with parameters A and CBCT. The most general form of generalized chi-squared distribution is obtained by extending the above consideration in two ways: firstly, to allow z to have a non-zero mean and, secondly, to include an additional linear combination of z in the definition of X.
Note that, in the above formulation, A and B need not be positive definite. However, the case where A is restricted to be at least positive semidefinite is an important one.
For the most general case, a reduction towards a common standard form can be made by using a representation of the following form:[4]
where D is a diagonal matrix and where x represents a vector of uncorrelated standard normal random variables.
Probability density and cumulative distribution functions
The probability density and cumulative distribution functions of a generalized chi-squared variable do not have simple closed-form expressions. However, numerical algorithms [4][2][5] and computer code for evaluating them have been published.
Applications
The generalized chi-squared is the distribution of statistical estimates in cases where the usual statistical theory does not hold. For example, if a predictive model is fitted by least squares, but the model errors have either autocorrelation or heteroscedasticity, then alternative models can be compared by relating changes in the sum of squares to an asymptotically valid generalized chi-squared distribution.[3]
Classifying normal samples using Gaussian discriminant analysis
If is a normal variable, its log likelihood is a quadratic form of , and is hence distributed as a generalized chi-squared. The log likelihood ratio that arises from one normal distribution versus another is also a quadratic form, so distributed as a generalized chi-squared.
In Gaussian discriminant analysis, samples from normal distributions are optimally separated by using a quadratic classifier, a boundary that is a quadratic function (e.g. the curve defined by setting the likelihood ratio between two Gaussians to 1). The classification error rates of different types (false positives and false negatives) are integrals of the normal distributions within the quadratic regions defined by this classifier. Since this is mathematically equivalent to integrating a quadratic form of a normal variable, the result is an integral of a generalized-chi-squared variable.
In signal processing
The following application arises in the context of Fourier analysis in signal processing, renewal theory in probability theory, and multi-antenna systems in wireless communication. The common factor of these areas is that the sum of exponentially distributed variables is of importance (or identically, the sum of squared magnitudes circular symmetric complex Gaussian variables).
If are k independent, circular symmetric complex Gaussian random variables with mean 0 and variance , then the random variable
has a generalized chi-squared distribution of a particular form. The difference from the standard chi-squared distribution is that are complex and can have different variances, and the difference from the more general generalized chi-squared distribution is that the relevant scaling matrix A is diagonal. If for all i, then , scaled down by (i.e. multiplied by ), has a chi-squared distribution, , also known as an Erlang distribution. If have distinct values for all i, then has the pdf[6]
If there are sets of repeated variances among , assume that they are divided into M sets, each representing a certain variance value. Denote to be the number of repetitions in each group. That is, the mth set contains variables that have variance It represents an arbitrary linear combination of independent -distributed random variables with different degrees of freedom:
The pdf of is[7]
where
with from the set of all partitions of (with ) defined as
See also
- Degrees of freedom (statistics)#Alternative
- Noncentral chi-squared distribution
- Chi-squared distribution
References
- Davies, R.B. (1973) Numerical inversion of a characteristic function. Biometrika, 60 (2), 415–417
- Davies, R,B. (1980) "Algorithm AS155: The distribution of a linear combination of χ2 random variables", Applied Statistics, 29, 323–333
- Jones, D.A. (1983) "Statistical analysis of empirical models fitted by optimisation", Biometrika, 70 (1), 67–88
- Sheil, J., O'Muircheartaigh, I. (1977) "Algorithm AS106: The distribution of non-negative quadratic forms in normal variables",Applied Statistics, 26, 92–98
- Imhof, J. P. (1961). "Computing the Distribution of Quadratic Forms in Normal Variables". Biometrika. 48 (3/4): 419–426. doi:10.2307/2332763. JSTOR 2332763.
- D. Hammarwall, M. Bengtsson, B. Ottersten (2008) "Acquiring Partial CSI for Spatially Selective Transmission by Instantaneous Channel Norm Feedback", IEEE Transactions on Signal Processing, 56, 1188–1204
- E. Björnson, D. Hammarwall, B. Ottersten (2009) "Exploiting Quantized Channel Norm Feedback through Conditional Statistics in Arbitrarily Correlated MIMO Systems", IEEE Transactions on Signal Processing, 57, 4027–4041