1 42 polytope
In 8-dimensional geometry, the 142 is a uniform 8-polytope, constructed within the symmetry of the E8 group.
 421 |
 142 |
 241 |
 Rectified 421 |
 Rectified 142 |
 Rectified 241 |
 Birectified 421 |
 Trirectified 421 | |
| Orthogonal projections in E6 Coxeter plane | ||
|---|---|---|
Its Coxeter symbol is 142, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequences.
The rectified 142 is constructed by points at the mid-edges of the 142 and is the same as the birectified 241, and the quadrirectified 421.
These polytopes are part of a family of 255 (28 − 1) convex uniform polytopes in 8-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
142 polytope
| 142 | |
|---|---|
| Type | Uniform 8-polytope |
| Family | 1k2 polytope |
| Schläfli symbol | {3,34,2} |
| Coxeter symbol | 142 |
| Coxeter diagrams | |
| 7-faces | 2400: 240 132 2160 141 |
| 6-faces | 106080: 6720 122 30240 131 69120 {35} |
| 5-faces | 725760: 60480 112 181440 121 483840 {34} |
| 4-faces | 2298240: 241920 102 604800 111 1451520 {33} |
| Cells | 3628800: 1209600 101 2419200 {32} |
| Faces | 2419200 {3} |
| Edges | 483840 |
| Vertices | 17280 |
| Vertex figure | t2{36} |
| Petrie polygon | 30-gon |
| Coxeter group | E8, [34,2,1] |
| Properties | convex |
The 142 is composed of 2400 facets: 240 132 polytopes, and 2160 7-demicubes (141). Its vertex figure is a birectified 7-simplex.
This polytope, along with the demiocteract, can tessellate 8-dimensional space, represented by the symbol 152, and Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Alternate names
- E. L. Elte (1912) excluded this polytope from his listing of semiregular polytopes, because it has more than two types of 6-faces, but under his naming scheme it would be called V17280 for its 17280 vertices.[1]
- Coxeter named it 142 for its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node branch.
- Diacositetracont-dischiliahectohexaconta-zetton (acronym bif) - 240-2160 facetted polyzetton (Jonathan Bowers)[2]
Coordinates
The 17280 vertices can be defined as sign and location permutations of:
All sign combinations (32): (280×32=8960 vertices)
- (4, 2, 2, 2, 2, 0, 0, 0)
Half of the sign combinations (128): ((1+8+56)×128=8320 vertices)
- (2, 2, 2, 2, 2, 2, 2, 2)
- (5, 1, 1, 1, 1, 1, 1, 1)
- (3, 3, 3, 1, 1, 1, 1, 1)
The edge length is 2√2 in this coordinate set, and the polytope radius is 4√2.
Construction
It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 8-dimensional space.
The facet information can be extracted from its Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Removing the node on the end of the 2-length branch leaves the 7-demicube, 141, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Removing the node on the end of the 4-length branch leaves the 132, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the birectified 7-simplex, 042, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Seen in a configuration matrix, the element counts can be derived by mirror removal and ratios of Coxeter group orders.[3]
| E8 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | k-figure | notes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A7 | ( ) | f0 | 17280 | 56 | 420 | 280 | 560 | 70 | 280 | 420 | 56 | 168 | 168 | 28 | 56 | 28 | 8 | 8 | 2r{36} | E8/A7 = 192*10!/8! = 17280 | |
| A4A2A1 | { } | f1 | 2 | 483840 | 15 | 15 | 30 | 5 | 30 | 30 | 10 | 30 | 15 | 10 | 15 | 3 | 5 | 3 | {3}x{3,3,3} | E8/A4A2A1 = 192*10!/5!/2/2 = 483840 | |
| A3A2A1 | {3} | f2 | 3 | 3 | 2419200 | 2 | 4 | 1 | 8 | 6 | 4 | 12 | 4 | 6 | 8 | 1 | 4 | 2 | {3.3}v{ } | E8/A3A2A1 = 192*10!/4!/3!/2 = 2419200 | |
| A3A3 | 110 | f3 | 4 | 6 | 4 | 1209600 | * | 1 | 4 | 0 | 4 | 6 | 0 | 6 | 4 | 0 | 4 | 1 | {3,3}v( ) | E8/A3A3 = 192*10!/4!/4! = 1209600 | |
| A3A2A1 | 4 | 6 | 4 | * | 2419200 | 0 | 2 | 3 | 1 | 6 | 3 | 3 | 6 | 1 | 3 | 2 | {3}v{ } | E8/A3A2A1 = 192*10!/4!/3!/2 = 2419200 | |||
| A4A3 | 120 | f4 | 5 | 10 | 10 | 5 | 0 | 241920 | * | * | 4 | 0 | 0 | 6 | 0 | 0 | 4 | 0 | {3,3} | E8/A4A3 = 192*10!/4!/4! = 241920 | |
| D4A2 | 111 | 8 | 24 | 32 | 8 | 8 | * | 604800 | * | 1 | 3 | 0 | 3 | 3 | 0 | 3 | 1 | {3}v( ) | E8/D4A2 = 192*10!/8/4!/3! = 604800 | ||
| A4A1A1 | 120 | 5 | 10 | 10 | 0 | 5 | * | * | 1451520 | 0 | 2 | 2 | 1 | 4 | 1 | 2 | 2 | { }v{ } | E8/A4A1A1 = 192*10!/5!/2/2 = 1451520 | ||
| D5A2 | 121 | f5 | 16 | 80 | 160 | 80 | 40 | 16 | 10 | 0 | 60480 | * | * | 3 | 0 | 0 | 3 | 0 | {3} | E8/D5A2 = 192*10!/16/5!/3! = 40480 | |
| D5A1 | 16 | 80 | 160 | 40 | 80 | 0 | 10 | 16 | * | 181440 | * | 1 | 2 | 0 | 2 | 1 | { }v( ) | E8/D5A1 = 192*10!/16/5!/2 = 181440 | |||
| A5A1 | 130 | 6 | 15 | 20 | 0 | 15 | 0 | 0 | 6 | * | * | 483840 | 0 | 2 | 1 | 1 | 2 | E8/A5A1 = 192*10!/6!/2 = 483840 | |||
| E6A1 | 122 | f6 | 72 | 720 | 2160 | 1080 | 1080 | 216 | 270 | 216 | 27 | 27 | 0 | 6720 | * | * | 2 | 0 | { } | E8/E6A1 = 192*10!/72/6!/2 = 6720 | |
| D6 | 131 | 32 | 240 | 640 | 160 | 480 | 0 | 60 | 192 | 0 | 12 | 32 | * | 30240 | * | 1 | 1 | E8/D6 = 192*10!/32/6! = 30240 | |||
| A6A1 | 140 | 7 | 21 | 35 | 0 | 35 | 0 | 0 | 21 | 0 | 0 | 7 | * | * | 69120 | 0 | 2 | E8/A6A1 = 192*10!/7!/2 = 69120 | |||
| E7 | 132 | f7 | 576 | 10080 | 40320 | 20160 | 30240 | 4032 | 7560 | 12096 | 756 | 1512 | 2016 | 56 | 126 | 0 | 240 | * | ( ) | E8/E7 = 192*10!/72/8! = 240 | |
| D7 | 141 | 64 | 672 | 2240 | 560 | 2240 | 0 | 280 | 1344 | 0 | 84 | 448 | 0 | 14 | 64 | * | 2160 | E8/D7 = 192*10!/64/7! = 2160 | |||
Projections
- u = (1, φ, 0, −1, φ, 0,0,0)
- v = (φ, 0, 1, φ, 0, −1,0,0)
- w = (0, 1, φ, 0, −1, φ,0,0)
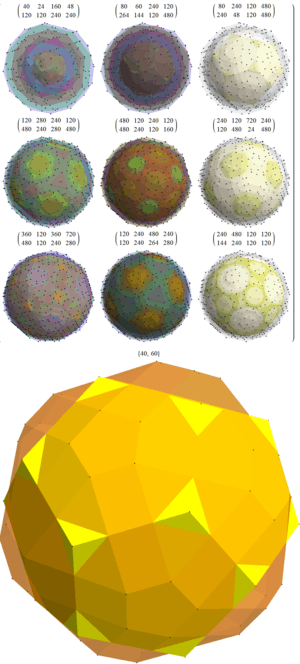
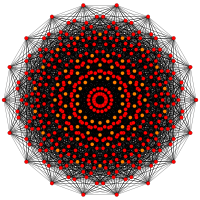
Orthographic projections are shown for the sub-symmetries of E8: E7, E6, B8, B7, B6, B5, B4, B3, B2, A7, and A5 Coxeter planes, as well as two more symmetry planes of order 20 and 24. Vertices are shown as circles, colored by their order of overlap in each projective plane.
| E8 [30] |
E7 [18] |
E6 [12] |
|---|---|---|
 (1) |
 (1,3,6) |
 (8,16,24,32,48,64,96) |
| [20] | [24] | [6] |
 |
 |
 (1,2,3,4,5,6,7,8,10,11,12,14,16,18,19,20) |
| D3 / B2 / A3 [4] |
D4 / B3 / A2 [6] |
D5 / B4 [8] |
|---|---|---|
 (32,160,192,240,480,512,832,960) |
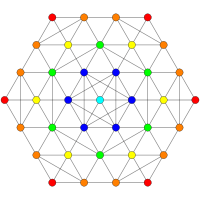 (72,216,432,720,864,1080) |
 (8,16,24,32,48,64,96) |
| D6 / B5 / A4 [10] |
D7 / B6 [12] |
D8 / B7 / A6 [14] |
 |
 |
 |
| B8 [16/2] |
A5 [6] |
A7 [8] |
 |
 |
 |
Related polytopes and honeycombs
| 1k2 figures in n dimensions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Euclidean | Hyperbolic | ||||||||
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Coxeter group |
E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 = = E8+ | E10 = = E8++ | |||
| Coxeter diagram |
|||||||||||
| Symmetry (order) |
[3−1,2,1] | [30,2,1] | [31,2,1] | [[3<sup>2,2,1</sup>]] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Order | 12 | 120 | 1,920 | 103,680 | 2,903,040 | 696,729,600 | ∞ | ||||
| Graph |  |
 |
 |
 |
 |
 |
- | - | |||
| Name | 1−1,2 | 102 | 112 | 122 | 132 | 142 | 152 | 162 | |||
Rectified 142 polytope
| Rectified 142 | |
|---|---|
| Type | Uniform 8-polytope |
| Schläfli symbol | t1{3,34,2} |
| Coxeter symbol | 0421 |
| Coxeter diagrams | |
| 7-faces | 19680 |
| 6-faces | 382560 |
| 5-faces | 2661120 |
| 4-faces | 9072000 |
| Cells | 16934400 |
| Faces | 16934400 |
| Edges | 7257600 |
| Vertices | 483840 |
| Vertex figure | {3,3,3}×{3}×{} |
| Coxeter group | E8, [34,2,1] |
| Properties | convex |
The rectified 142 is named from being a rectification of the 142 polytope, with vertices positioned at the mid-edges of the 142. It can also be called a 0421 polytope with the ring at the center of 3 branches of length 4, 2, and 1.
Alternate names
- 0421 polytope
- Birectified 241 polytope
- Quadrirectified 421 polytope
- Rectified diacositetracont-dischiliahectohexaconta-zetton as a rectified 240-2160 facetted polyzetton (acronym buffy) (Jonathan Bowers)[4]
Construction
It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 8-dimensional space.
The facet information can be extracted from its Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Removing the node on the end of the 1-length branch leaves the birectified 7-simplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Removing the node on the end of the 2-length branch leaves the 7-demicube, 141, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Removing the node on the end of the 3-length branch leaves the 132, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the 5-cell-triangle duoprism prism, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Seen in a configuration matrix, the element counts can be derived by mirror removal and ratios of Coxeter group orders.[5]
| E8 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | k-figure | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A4A2A1 | ( ) | f0 | 483840 | 30 | 30 | 15 | 60 | 10 | 15 | 60 | 30 | 60 | 5 | 20 | 30 | 60 | 30 | 30 | 10 | 20 | 30 | 30 | 15 | 6 | 10 | 10 | 15 | 6 | 3 | 5 | 2 | 3 | {3,3,3}x{3,3}x{} | |
| A3A1A1 | { } | f1 | 2 | 7257600 | 2 | 1 | 4 | 1 | 2 | 8 | 4 | 6 | 1 | 4 | 8 | 12 | 6 | 4 | 4 | 6 | 12 | 8 | 4 | 1 | 6 | 4 | 8 | 2 | 1 | 4 | 1 | 2 | ||
| A3A2 | {3} | f2 | 3 | 3 | 4838400 | * | * | 1 | 1 | 4 | 0 | 0 | 1 | 4 | 4 | 6 | 0 | 0 | 4 | 6 | 6 | 4 | 0 | 0 | 6 | 4 | 4 | 1 | 0 | 4 | 1 | 1 | ||
| A3A2A1 | 3 | 3 | * | 2419200 | * | 0 | 2 | 0 | 4 | 0 | 1 | 0 | 8 | 0 | 6 | 0 | 4 | 0 | 12 | 0 | 4 | 0 | 6 | 0 | 8 | 0 | 1 | 4 | 0 | 2 | ||||
| A2A2A1 | 3 | 3 | * | * | 9676800 | 0 | 0 | 2 | 1 | 3 | 0 | 1 | 2 | 6 | 3 | 3 | 1 | 3 | 6 | 6 | 3 | 1 | 3 | 3 | 6 | 2 | 1 | 3 | 1 | 2 | ||||
| A3A3 | 0200 | f3 | 4 | 6 | 4 | 0 | 0 | 1209600 | * | * | * | * | 1 | 4 | 0 | 0 | 0 | 0 | 4 | 6 | 0 | 0 | 0 | 0 | 6 | 4 | 0 | 0 | 0 | 4 | 1 | 0 | ||
| 0110 | 6 | 12 | 4 | 4 | 0 | * | 1209600 | * | * | * | 1 | 0 | 4 | 0 | 0 | 0 | 4 | 0 | 6 | 0 | 0 | 0 | 6 | 0 | 4 | 0 | 0 | 4 | 0 | 1 | ||||
| A3A2 | 6 | 12 | 4 | 0 | 4 | * | * | 4838400 | * | * | 0 | 1 | 1 | 3 | 0 | 0 | 1 | 3 | 3 | 3 | 0 | 0 | 3 | 3 | 3 | 1 | 0 | 3 | 1 | 1 | ||||
| A3A2A1 | 6 | 12 | 0 | 4 | 4 | * | * | * | 2419200 | * | 0 | 0 | 2 | 0 | 3 | 0 | 1 | 0 | 6 | 0 | 3 | 0 | 3 | 0 | 6 | 0 | 1 | 3 | 0 | 2 | ||||
| A3A1A1 | 0200 | 4 | 6 | 0 | 0 | 4 | * | * | * | * | 7257600 | 0 | 0 | 0 | 2 | 1 | 2 | 0 | 1 | 2 | 4 | 2 | 1 | 1 | 2 | 4 | 2 | 1 | 2 | 1 | 2 | |||
| A4A3 | 0210 | f4 | 10 | 30 | 20 | 10 | 0 | 5 | 5 | 0 | 0 | 0 | 241920 | * | * | * | * | * | 4 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | ||
| A4A2 | 10 | 30 | 20 | 0 | 10 | 5 | 0 | 5 | 0 | 0 | * | 967680 | * | * | * | * | 1 | 3 | 0 | 0 | 0 | 0 | 3 | 3 | 0 | 0 | 0 | 3 | 1 | 0 | ||||
| D4A2 | 0111 | 24 | 96 | 32 | 32 | 32 | 0 | 8 | 8 | 8 | 0 | * | * | 604800 | * | * | * | 1 | 0 | 3 | 0 | 0 | 0 | 3 | 0 | 3 | 0 | 0 | 3 | 0 | 1 | |||
| A4A1 | 0210 | 10 | 30 | 10 | 0 | 20 | 0 | 0 | 5 | 0 | 5 | * | * | * | 2903040 | * | * | 0 | 1 | 1 | 2 | 0 | 0 | 1 | 2 | 2 | 1 | 0 | 2 | 1 | 1 | |||
| A4A1A1 | 10 | 30 | 0 | 10 | 20 | 0 | 0 | 0 | 5 | 5 | * | * | * | * | 1451520 | * | 0 | 0 | 2 | 0 | 2 | 0 | 1 | 0 | 4 | 0 | 1 | 2 | 0 | 2 | ||||
| A4A1 | 0300 | 5 | 10 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 5 | * | * | * | * | * | 2903040 | 0 | 0 | 0 | 2 | 1 | 1 | 0 | 1 | 2 | 2 | 1 | 1 | 1 | 2 | |||
| D5A2 | 0211 | f5 | 80 | 480 | 320 | 160 | 160 | 80 | 80 | 80 | 40 | 0 | 16 | 16 | 10 | 0 | 0 | 0 | 60480 | * | * | * | * | * | 3 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | {3} | |
| A5A1 | 0220 | 20 | 90 | 60 | 0 | 60 | 15 | 0 | 30 | 0 | 15 | 0 | 6 | 0 | 6 | 0 | 0 | * | 483840 | * | * | * | * | 1 | 2 | 0 | 0 | 0 | 2 | 1 | 0 | { }v() | ||
| D5A1 | 0211 | 80 | 480 | 160 | 160 | 320 | 0 | 40 | 80 | 80 | 80 | 0 | 0 | 10 | 16 | 16 | 0 | * | * | 181440 | * | * | * | 1 | 0 | 2 | 0 | 0 | 2 | 0 | 1 | |||
| A5 | 0310 | 15 | 60 | 20 | 0 | 60 | 0 | 0 | 15 | 0 | 30 | 0 | 0 | 0 | 6 | 0 | 6 | * | * | * | 967680 | * | * | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | ( )v( )v() | ||
| A5A1 | 15 | 60 | 0 | 20 | 60 | 0 | 0 | 0 | 15 | 30 | 0 | 0 | 0 | 0 | 6 | 6 | * | * | * | * | 483840 | * | 0 | 0 | 2 | 0 | 1 | 1 | 0 | 2 | { }v() | |||
| 0400 | 6 | 15 | 0 | 0 | 20 | 0 | 0 | 0 | 0 | 15 | 0 | 0 | 0 | 0 | 0 | 6 | * | * | * | * | * | 483840 | 0 | 0 | 0 | 2 | 1 | 0 | 1 | 2 | ||||
| E6A1 | 0221 | f6 | 720 | 6480 | 4320 | 2160 | 4320 | 1080 | 1080 | 2160 | 1080 | 1080 | 216 | 432 | 270 | 432 | 216 | 0 | 27 | 72 | 27 | 0 | 0 | 0 | 6720 | * | * | * | * | 2 | 0 | 0 | { } | |
| A6 | 0320 | 35 | 210 | 140 | 0 | 210 | 35 | 0 | 105 | 0 | 105 | 0 | 21 | 0 | 42 | 0 | 21 | 0 | 7 | 0 | 7 | 0 | 0 | * | 138240 | * | * | * | 1 | 1 | 0 | |||
| D6 | 0311 | 240 | 1920 | 640 | 640 | 1920 | 0 | 160 | 480 | 480 | 960 | 0 | 0 | 60 | 192 | 192 | 192 | 0 | 0 | 12 | 32 | 32 | 0 | * | * | 30240 | * | * | 1 | 0 | 1 | |||
| A6 | 0410 | 21 | 105 | 35 | 0 | 140 | 0 | 0 | 35 | 0 | 105 | 0 | 0 | 0 | 21 | 0 | 42 | 0 | 0 | 0 | 7 | 0 | 7 | * | * | * | 138240 | * | 0 | 1 | 1 | |||
| A6A1 | 21 | 105 | 0 | 35 | 140 | 0 | 0 | 0 | 35 | 105 | 0 | 0 | 0 | 0 | 21 | 42 | 0 | 0 | 0 | 0 | 7 | 7 | * | * | * | * | 69120 | 0 | 0 | 2 | ||||
| E7 | 0321 | f7 | 10080 | 120960 | 80640 | 40320 | 120960 | 20160 | 20160 | 60480 | 30240 | 60480 | 4032 | 12096 | 7560 | 24192 | 12096 | 12096 | 756 | 4032 | 1512 | 4032 | 2016 | 0 | 56 | 576 | 126 | 0 | 0 | 240 | * | * | ( ) | |
| A7 | 0420 | 56 | 420 | 280 | 0 | 560 | 70 | 0 | 280 | 0 | 420 | 0 | 56 | 0 | 168 | 0 | 168 | 0 | 28 | 0 | 56 | 0 | 28 | 0 | 8 | 0 | 8 | 0 | * | 17280 | * | |||
| D7 | 0411 | 672 | 6720 | 2240 | 2240 | 8960 | 0 | 560 | 2240 | 2240 | 6720 | 0 | 0 | 280 | 1344 | 1344 | 2688 | 0 | 0 | 84 | 448 | 448 | 448 | 0 | 0 | 14 | 64 | 64 | * | * | 2160 | |||
Projections
Orthographic projections are shown for the sub-symmetries of B6, B5, B4, B3, B2, A7, and A5 Coxeter planes. Vertices are shown as circles, colored by their order of overlap in each projective plane.
(Planes for E8: E7, E6, B8, B7, [24] are not shown for being too large to display.)
| D3 / B2 / A3 [4] |
D4 / B3 / A2 [6] |
D5 / B4 [8] |
|---|---|---|
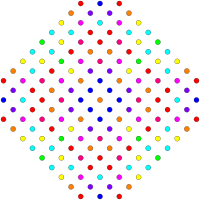 |
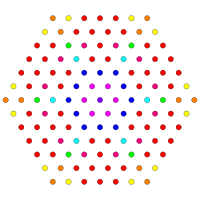 |
 |
| D6 / B5 / A4 [10] |
D7 / B6 [12] |
[6] |
 |
 |
 |
| A5 [6] |
A7 [8] |
[20] |
 |
 |
 |
See also
- List of E8 polytopes
Notes
- Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen
- Klitzing, (o3o3o3x *c3o3o3o3o - bif)
- Coxeter, Regular Polytopes, 11.8 Gossett figures in six, seven, and eight dimensions, p. 202-203
- Klitzing, (o3o3o3x *c3o3o3o3o - buffy)
- Coxeter, Regular Polytopes, 11.8 Gossett figures in six, seven, and eight dimensions, p. 202-203
References
- H. S. M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Klitzing, Richard. "8D Uniform polyzetta". o3o3o3x *c3o3o3o3o - bif, o3o3o3x *c3o3o3o3o - buffy
Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||