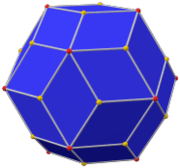
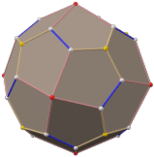
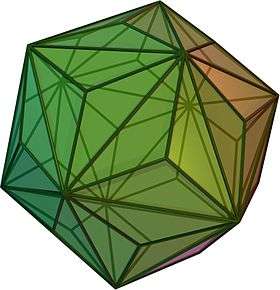
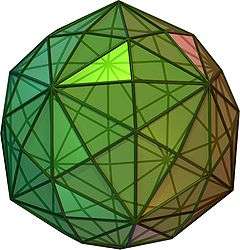
Deltoidal hexecontahedron

Deltoidal hexecontahedron

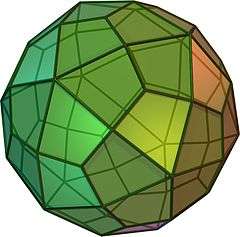click for spinning version
TypeCatalan
Conway notationoD or deD
Coxeter diagram
Face polygon
kite
Faces60
Edges120
Vertices62 = 12 + 20 + 30
Face configurationV3.4.5.4
Symmetry groupIh, H3, [5,3], (*532)
Rotation groupI, [5,3]+, (532)
Dihedral angle154° 7′ 17″
Propertiesconvex, face-transitive

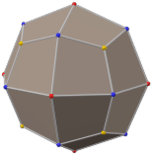
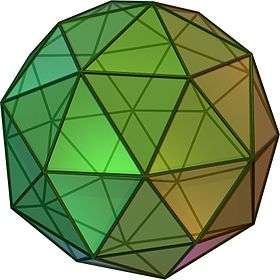
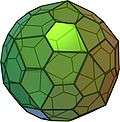
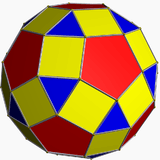rhombicosidodecahedron
(dual polyhedron)
Net

In geometry, a deltoidal hexecontahedron (also sometimes called a trapezoidal hexecontahedron, a strombic hexecontahedron, or a tetragonal hexacontahedron[1]) is a Catalan solid which is the dual polyhedron of the rhombicosidodecahedron, an Archimedean solid. It is one of six Catalan solids to not have a Hamiltonian path among its vertices.[2]

It is topologically identical to the nonconvex rhombic hexecontahedron.

Lengths and angles

The 60 faces are deltoids or kites. The short and long edges of each kite are in the ratio 1:7 + √5/6 ≈ 1:1.539344663...

The angle between two short edges is 118.267°. The opposite angle, between long edges, is 67.783°. The other two angles, between a short and a long edge each, are both 86.974°.

The dihedral angle between all faces is 154.12°.

Topology

Topologically, the deltoidal hexecontahedron is identical to the nonconvex rhombic hexecontahedron. The deltoidal hexecontahedron can be derived from a dodecahedron (or icosahedron) by pushing the face centers, edge centers and vertices out to different radii from the body center. The radii are chosen so that the resulting shape has planar kite faces each such that vertices go to degree-3 corners, faces to degree-five corners, and edge centers to degree-four points.

Orthogonal projections

The deltoidal hexecontahedron has 3 symmetry positions located on the 3 types of vertices:

Orthogonal projections
Projective
symmetry		 [2] [2] [2] [2] [6] [10]
Image
Dual
image

Variations

This figure from Perspectiva Corporum Regularium (1568) by Wenzel Jamnitzer can be seen as a deltoidal hexecontahedron.

The deltoidal hexecontahedron can be constructed from either the regular icosahedron or regular dodecahedron by adding verties mid-edge, and mid-face, and creating new edges from each edge center to the face centers. Conway polyhedron notation would give these as oI, and oD, ortho-icosahedron, and ortho-dodecahedron. These geometric variations exist as a continuum along one degree of freedom.

Spherical deltoidal hexecontahedron

When projected onto a sphere (see right), it can be seen that the edges make up the edges of an icosahedron and dodecahedron arranged in their dual positions.

This tiling is topologically related as a part of sequence of deltoidal polyhedra with face figure (V3.4.n.4), and continues as tilings of the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.

*n42 symmetry mutation of dual expanded tilings: V3.4.n.4
Symmetry
*n32
[n,3]		 Spherical Euclid. Compact hyperb. Paraco.
*232
[2,3]		 *332
[3,3]		 *432
[4,3]		 *532
[5,3]		 *632
[6,3]		 *732
[7,3]		 *832
[8,3]...		 *∞32
[∞,3]
Figure
Config.
V3.4.2.4
V3.4.3.4
V3.4.4.4
V3.4.5.4
V3.4.6.4
V3.4.7.4
V3.4.8.4
V3.4.∞.4

See also

References

  1. ↑ Conway, Symmetries of things, p.284-286
  2. ↑ http://mathworld.wolfram.com/ArchimedeanDualGraph.html
  • Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
  • The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 286, tetragonal hexecontahedron)
  • http://mathworld.wolfram.com/ArchimedeanDualGraph.html


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.