Parallellogram van Varignon
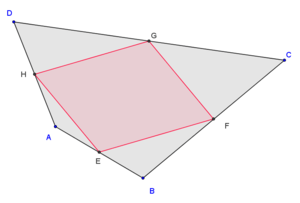
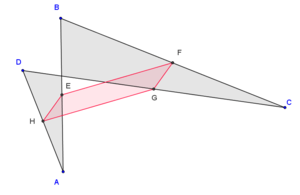
Bij een willekeurige vierhoek zijn de middens van de zijden de hoekpunten van een parallellogram. Dit parallellogram noemt men het parallellogram van Varignon, naar de Franse wiskundige Pierre Varignon (1654-1722). De stelling die het bestaan van dit parallellogram beschrijft noemt men de stelling van Varignon.

Het bewijs van deze stelling is eenvoudig. Stel de hoekpunten van de vierhoek zijn ABCD. Het lijnstuk EF dat het midden E van AB en het midden F van BC verbindt, is evenwijdig met AC. Dus is het lijnstuk GH dat de middens van G van CD en H van AD verbindt, evenwijdig met EF. Evenzo zijn EH en FG evenwijdig, en dus is EFGH een parallellogram.
Bij een gegeven parallellogram zijn er oneindig veel vierhoeken die deze als parallellogram van Varignon hebben, hieronder zijn zelfs oneindig veel koordenvierhoeken. De middelpunten van de omgeschreven cirkels van deze koordenvierhoeken liggen op de gelijkzijdige hyperbool, die omgeschreven is aan het gegeven parallellogram.
Afbeeldingen
Diverse vierhoeken met het bijbehorende parallellogram van Varignon
| Convexe vierhoek | Inspringende vierhoek | Gekruiste vierhoek |
|---|---|---|
|
|
|
|
Eigenschappen
Voor een convexe vierhoek geldt:
- De omtrek van het parallellogram van Varignon is gelijk aan de som van de lengten van de diagonalen van de oorspronkelijke vierhoek.
- De oppervlakte van het parallellogram van Varignon is gelijk aan de helft van de oppervlakte van de oorspronkelijke vierhoek.
Bronnen, noten en/of referenties
|