Gibbsverschijnsel

Benadering van de blokgolf met 5 harmonischen

Benadering van de blokgolf met 25 harmonischen

Benadering van de blokgolf met 125 harmonischen

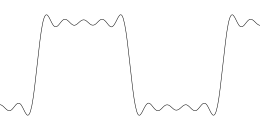
Het Gibbsverschijnsel betreft zowel het feit dat fouriersommen bij een sprongdiscontinuïteit overshoot vertonen, als dat deze overshoot niet uitsterft wanneer meer termen worden meegenomen.

De drie figuren aan de rechterkant laten het verschijnsel zien voor een blokgolf met hoogte ${\displaystyle \pi /4}$ met de fourierontwikkeling

${\displaystyle \sin(x)+{\tfrac {1}{3}}\sin(3x)+{\tfrac {1}{5}}\sin(5x)+\ldots }$.

Nauwkeuriger geformuleerd gaat het om de functie ${\displaystyle f}$ die voor elke ${\displaystyle n}$ de waarde ${\displaystyle \pi /4}$ aanneemt tussen ${\displaystyle 2n\pi }$ en ${\displaystyle (2n+1)\pi }$ en ${\displaystyle -\pi /4}$ tussen ${\displaystyle (2n+1)\pi }$ en ${\displaystyle (2n+2)\pi }$. Deze blokgolf heeft een dus een sprongdiscontinuïteit ter grootte ${\displaystyle \pi /2}$ in elk geheel veelvoud van ${\displaystyle \pi }$.

Zoals te zien is, vermindert, als het aantal termen toeneemt, de fout van de benadering zowel in breedte als in energie, maar convergeert deze niet naar 0, maar naar een vaste hoogte. Een berekening voor de blokgolf (zie Zygmund, hfst. 8.5., of de berekeningen aan het eind van dit artikel) geeft een expliciete formule voor de limiet. Het blijkt dat de fourierreeks de hoogte ${\displaystyle \pi /4}$ van de blokgolf overschrijdt met

${\displaystyle {\tfrac {1}{2}}\int _{0}^{\pi }{\frac {\sin t}{t}}\,{\rm {d}}t-{\tfrac {1}{4}}\pi ={\tfrac {1}{2}}\pi \cdot 0{,}089489872236\dots ,}$

wat ongeveer 9% van de spronggrootte is.

Meer algemeen: op elk sprongpunt van een stuksgewijze continu differentieerbare functie, zal de ${\displaystyle n}$-de partiële som van de fourierontwikeling voor zeer grote ${\displaystyle n}$ deze sprong met ongeveer ${\displaystyle 0{,}089489872236\dots }$ overschrijden aan de bovenkant en onderschrijden met dezelfde fractie aan de onderkant. De "sprong" in de partiële som van de fourierontwikeling zal dus ongeveer 18% groter zijn dan de sprong in de oorspronkelijke functie. Ter plaatse van de discontinuïteit zelf, zal de fourierreeks convergeren naar het midden van de sprong (ongeacht wat de werkelijke waarde van de oorspronkelijke functie is in dit punt). De grootheid

${\displaystyle \int _{0}^{\pi }{\frac {\sin t}{t}}\,{\rm {d}}t=1{,}851937051982\dots ={\tfrac {1}{2}}\pi +\pi \cdot 0{,}089489872236\dots }$

staat wel bekend als de Wilbraham-Gibbs-constante.

Het Gibbsverschijnsel werd voor het eerst opgemerkt en geanalyseerd door Henry Wilbraham. In 1848 publiceerde hij er een artikel over, dat echter onopgemerkt bleef in de wiskundige wereld.[4] Albert Michelson ontwikkelde in 1898 een apparaat dat de fourierreeks kon berekenen en weer synthetiseren. Een wijdverbreide mythe zegt dat toen de fouriercoëfficiënten voor een blokgolf werden ingevoerd in de machine, de grafiek zou zijn gaan oscilleren rond de discontinuïteiten. En omdat een fysiek apparaat onderhevig is aan fabricagefouten, zou Michelson ervan overtuigd zijn geweest dat de overshoot veroorzaakt werd door fouten in de machine. In feite waren de grafieken die de machine produceerde niet goed genoeg om duidelijk het Gibbsverschijnsel te tonen, en Michelson zal het niet opgemerkt hebben omdat hij geen melding maakt van dit verschijnsel in het artikel over zijn machine of in zijn latere brieven aan Nature. Geïnspireerd door een briefwisseling in Nature tussen Michelson en Love over de convergentie van de fourierreeks van de blokgolffunctie, publiceerde Gibbs in 1898 een kort briefje waarin hij wat vandaag de dag een zaagtand zou worden genoemd, beschouwde, en wees op het belangrijke verschil tussen de limiet van de grafieken van de partiële sommen van de fourierreeks, en de grafiek van de functie die de limiet is van die partiële sommen. In zijn eerste brief noemde Gibbs het Gibbsverschijnsel niet, en de limiet die hij beschreef voor de grafieken van de partiële sommen was inaccuraat. In 1899 publiceerde hij een correctie, waarin hij de overshoot beschreef in het discontinuïteitspunt (Nature: 27 april 1899, p. 606). In 1906 gaf Maxime Bôcher een uitgebreide statistische analyse van die overshoot, die hij het "Gibbsverschijnsel" noemde.[5]

Informeel weerspiegelt het verschijnsel de moeilijkheden die inherent zijn aan het benaderen van een discontinue functie door een eindige reeks continue sinussen en cosinussen. Daarbij ligt de nadruk op eindige, want hoewel elke partiële som van de fourierreeks de overschrijding vertoont in de benadering van de functie, doet de limiet van de partiële sommen dat niet. Het punt waar de maximale overschrijding optreedt, nadert meer en meer de discontinuïteit als het aantal termen in de partiële som toeneemt. Zodra de overshoot een punt gepasseerd is, convergeert de fourierreeks in dat punt. Er is sprake van puntsgewijze convergentie, maar niet van uniforme convergentie.

Voor een stuksgewijze ${\displaystyle C^{1}}$-functie convergeert de fourierreeks naar de functie in elk punt, behalve in de sprongdiscontinuïteiten. Voor deze sprongdiscontinuïteiten is er convergentie naar het gemiddelde van de waarden van de functie aan weerszijden van de sprong. Dit is een gevolg van de stelling van Dirichlet[6]

Zij ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ een stuksgewijs continue, differentieerbare en periodieke functie met periode ${\displaystyle T}$, die in het punt ${\displaystyle x_{0}}$ een sprongdiscontinuïteit heeft:

${\displaystyle f(x_{0}^{+})-f(x_{0}^{-})=a\neq 0.}$

Noem voor de eenvoud van notatie ${\displaystyle \omega =2\pi /L}$. De fouriergetransformeerde van ${\displaystyle f}$ wordt gegeven door de rij:

${\displaystyle F(n)={\frac {1}{L}}\int _{0}^{L}f(x)e^{-i\omega nx}\,{\rm {d}}x}$

en de ${\displaystyle N}$-de partiële som van de fourierreeks door:

${\displaystyle S_{N}(x)=\sum _{-N\leq n\leq N}F(n)e^{i\omega nx}}$

Dan geldt:

${\displaystyle \lim _{N\to \infty }S_{N}\left(x_{0}+{\frac {L}{2N}}\right)=f(x_{0}^{+})+a\cdot 0{,}089489872236\dots }$

en

${\displaystyle \lim _{N\to \infty }S_{N}\left(x_{0}-{\frac {L}{2N}}\right)=f(x_{0}^{-})-a\cdot 0{,}089489872236\dots }$,

maar

${\displaystyle \lim _{N\to \infty }S_{N}(x_{0})={\frac {f(x_{0}^{-})+f(x_{0}^{+})}{2}}.}$

Meer algemeen geldt voor elke rij ${\displaystyle (x_{n})}$ reële getallen die convergeert naar ${\displaystyle x_{0}}$ dat als ${\displaystyle a>0}$ is:

${\displaystyle \limsup _{N\to \infty }S_{N}(x_{N})\leq f(x_{0}^{+})+a\cdot 0{,}089489872236\dots }$

en

${\displaystyle \liminf _{N\to \infty }S_{N}f(x_{N})\geq f(x_{0}^{-})-a\cdot 0{,}089489872236\dots .}$

Als ${\displaystyle a<0}$ is, gelden analoge relaties.