Truncated cuboctahedron
In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges. Since each of its faces has point symmetry (equivalently, 180° rotational symmetry), the truncated cuboctahedron is a zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.
| Truncated cuboctahedron | |
|---|---|
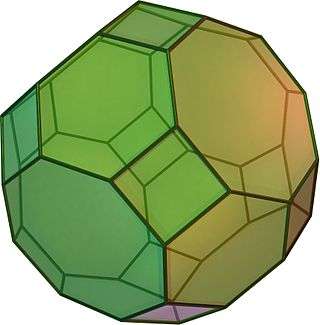 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 26, E = 72, V = 48 (χ = 2) |
| Faces by sides | 12{4}+8{6}+6{8} |
| Conway notation | bC or taC |
| Schläfli symbols | tr{4,3} or |
| t0,1,2{4,3} | |
| Wythoff symbol | 2 3 4 | |
| Coxeter diagram | |
| Symmetry group | Oh, B3, [4,3], (*432), order 48 |
| Rotation group | O, [4,3]+, (432), order 24 |
| Dihedral angle | 4-6: arccos(−√6/3) = 144°44′08″ 4-8: arccos(−√2/3) = 135° 6-8: arccos(−√3/3) = 125°15′51″ |
| References | U11, C23, W15 |
| Properties | Semiregular convex zonohedron |
 Colored faces |
 4.6.8 (Vertex figure) |
 Disdyakis dodecahedron (dual polyhedron) |
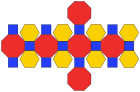 Net |

Names
|
The name truncated cuboctahedron, given originally by Johannes Kepler, is misleading. An actual truncation of a cuboctahedron has rectangles instead of squares. This nonuniform polyhedron is topologically equivalent to the Archimedean solid. Alternate interchangeable names are:
|
 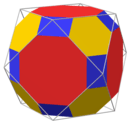 Cuboctahedron and its truncation |
There is a nonconvex uniform polyhedron with a similar name, the nonconvex great rhombicuboctahedron.
Cartesian coordinates
The Cartesian coordinates for the vertices of a truncated cuboctahedron having edge length 2 and centered at the origin are all permutations of:
- (±1, ±(1 + √2), ±(1 + 2√2))
Area and volume
The area A and the volume V of the truncated cuboctahedron of edge length a are:
Dissection
The truncated cuboctahedron is the convex hull of a rhombicuboctahedron with cubes above its 12 squares on 2-fold symmetry axes. The rest of its space can be dissected into 6 square cupolas below the octagons and 8 triangular cupolas below the hexagons.
A dissected truncated cuboctahedron can create a genus 5, 7 or 11 Stewart toroid by removing the central rhombicuboctahedron and either the square cupolas, the triangular cupolas or the 12 cubes respectively. Many other lower symmetry toroids can also be constructed by removing a subset of these dissected components. For example, removing half of the triangular cupolas creates a genus 3 torus, which (if they are chosen appropriately) has tetrahedral symmetry.[4][5]
| Stewart toroids | |||
|---|---|---|---|
| Genus 3 | Genus 5 | Genus 7 | Genus 11 |
 |
 |
 |
 |
Uniform colorings
There is only one uniform coloring of the faces of this polyhedron, one color for each face type.
A 2-uniform coloring, with tetrahedral symmetry, exists with alternately colored hexagons.
Orthogonal projections



The truncated cuboctahedron has two special orthogonal projections in the A2 and B2 Coxeter planes with [6] and [8] projective symmetry, and numerous [2] symmetries can be constructed from various projected planes relative to the polyhedron elements.
| Centered by | Vertex | Edge 4-6 |
Edge 4-8 |
Edge 6-8 |
Face normal 4-6 |
|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
 |
| Projective symmetry |
[2]+ | [2] | [2] | [2] | [2] |
| Centered by | Face normal Square |
Face normal Octagon |
Face Square |
Face Hexagon |
Face Octagon |
| Image |  |
 |
 |
 |
 |
| Projective symmetry |
[2] | [2] | [2] | [6] | [4] |
Spherical tiling
The truncated cuboctahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
 |
 |
 |
 |
| Orthogonal projection | square-centered | hexagon-centered | octagon-centered |
|---|---|---|---|
| Stereographic projections | |||
Full octahedral group

Like many other solids the truncated octahedron has full octahedral symmetry - but its relationship with the full octahedral group is closer than that: Its 48 vertices correspond to the elements of the group, and each face of its dual is a fundamental domain of the group.
The image on the right shows the 48 permutations in the group applied to an example object (namely the light JF compound on the left). The 24 light elements are rotations, and the dark ones are their reflections.
The edges of the solid correspond to the 9 reflections in the group:
- Those between octagons and squares correspond to the 3 reflections between opposite octagons.
- Hexagon edges correspond to the 6 reflections between opposite squares.
- (There are no reflections between opposite hexagons.)
The subgroups correspond to solids that share the respective vertices of the truncated octahedron.
E.g. the 3 subgroups with 24 elements correspond to a nonuniform snub cube with chiral octahedral symmetry, a nonuniform truncated octahedron with full tetrahedral symmetry and a nonuniform rhombicuboctahedron with pyritohedral symmetry (the cantic snub octahedron).
The unique subgroup with 12 elements is the alternating group A4. It corresponds to a nonuniform icosahedron with chiral tetrahedral symmetry.
| Subgroups and corresponding solids | ||||
|---|---|---|---|---|
 |
 |
 |
 |
 |
| all 48 vertices | 24 vertices | 12 vertices | ||
Related polyhedra
 |
 |
| Bowtie tetrahedron and cube contain two trapezoidal faces in place of the square.[6] | |
The truncated cuboctahedron is one of a family of uniform polyhedra related to the cube and regular octahedron.
| Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duals to uniform polyhedra | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
This polyhedron can be considered a member of a sequence of uniform patterns with vertex configuration (4.6.2p) and Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
| *n32 symmetry mutations of omnitruncated tilings: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Figures |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals | 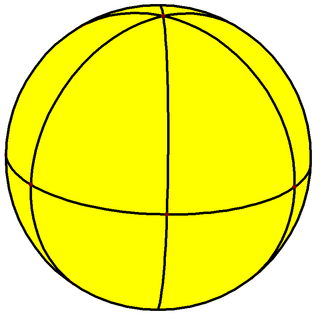 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
| *n42 symmetry mutation of omnitruncated tilings: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | |
| Omnitruncated figure |
 4.8.4 |
 4.8.6 |
 4.8.8 |
 4.8.10 |
 4.8.12 |
 4.8.14 |
 4.8.16 |
 4.8.∞ |
| Omnitruncated duals |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
It is first in a series of cantitruncated hypercubes:
  |
  |
  |
  |
  |
  |
| Truncated cuboctahedron | Cantitruncated tesseract | Cantitruncated 5-cube | Cantitruncated 6-cube | Cantitruncated 7-cube | Cantitruncated 8-cube |
Truncated cuboctahedral graph
| Truncated cuboctahedral graph | |
|---|---|
 4-fold symmetry | |
| Vertices | 48 |
| Edges | 72 |
| Automorphisms | 48 |
| Chromatic number | 2 |
| Properties | Cubic, Hamiltonian, regular, zero-symmetric |
| Table of graphs and parameters | |
In the mathematical field of graph theory, a truncated cuboctahedral graph (or great rhombcuboctahedral graph) is the graph of vertices and edges of the truncated cuboctahedron, one of the Archimedean solids. It has 48 vertices and 72 edges, and is a zero-symmetric and cubic Archimedean graph.[7]
See also
| Wikimedia Commons has media related to Truncated cuboctahedron. |
- Cube
- Cuboctahedron
- Octahedron
- Truncated icosidodecahedron
- Truncated octahedron – truncated tetratetrahedron
References
- Wenninger, Magnus (1974), Polyhedron Models, Cambridge University Press, ISBN 978-0-521-09859-5, MR 0467493 (Model 15, p. 29)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9, p. 82)
- Cromwell, P.; Polyhedra, CUP hbk (1997), pbk. (1999). (p. 82)
- B. M. Stewart, Adventures Among the Toroids (1970) ISBN 978-0-686-11936-4
- Doskey, Alex. "Adventures Among the Toroids - Chapter 5 - Simplest (R)(A)(Q)(T) Toroids of genus p=1". www.doskey.com.
- Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons Craig S. Kaplan
- Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
- Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
External links
- Eric W. Weisstein, Great rhombicuboctahedron (Archimedean solid) at MathWorld.
- Klitzing, Richard. "3D convex uniform polyhedra x3x4x - girco".
- Editable printable net of a truncated cuboctahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- great Rhombicuboctahedron: paper strips for plaiting














