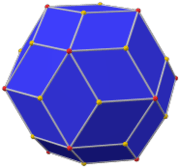
Pentakis dodecahedron
In geometry, a pentakis dodecahedron or kisdodecahedron is the polyhedron created by attaching a pentagonal pyramid to each face of a regular dodecahedron; that is, it is the Kleetope of the dodecahedron. This interpretation is expressed in its name.[1] There are in fact several topologically equivalent but geometrically distinct kinds of pentakis dodecahedron, depending on the height of the pentagonal pyramids. These include:
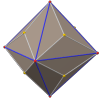
- The usual Catalan pentakis dodecahedron, a convex hexecontahedron with sixty isosceles triangular faces illustrated in the sidebar figure. It is a Catalan solid, dual to the truncated icosahedron, an Archimedean solid. The critical height of each of the pyramids above the faces of the original unit dodecahedron is
- At this size, the dihedral angle between all neighbouring triangular faces is equal to the value in the table above. Flatter pyramids have higher intra-pyramid dihedrals and taller pyramids have higher inter-pyramid dihedrals.
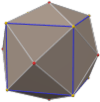
- As the heights of the pentagonal pyramids are raised, at a certain point adjoining pairs of triangular faces merge to become rhombi, and the shape becomes a rhombic triacontahedron.
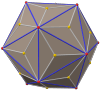
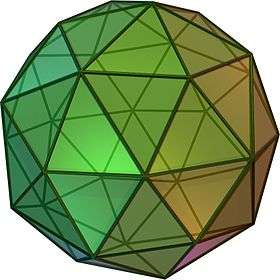
- As the height is raised further, the shape becomes non-convex. In particular, an equilateral or deltahedron version of the pentakis dodecahedron, which has sixty equilateral triangular faces as shown in the adjoining figure, is slightly non-convex due to its taller pyramids (note, for example, the negative dihedral angle at the upper left of the figure).
| Pentakis dodecahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | kD |
| Face type | V5.6.6 isosceles triangle |
| Faces | 60 |
| Edges | 90 |
| Vertices | 32 |
| Vertices by type | 20{6}+12{5} |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 156°43′07″ arccos(−80 + 9√5/109) |
| Properties | convex, face-transitive |
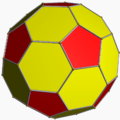 Truncated icosahedron (dual polyhedron) |
 Net |

Other more non-convex geometric variants include:



If one affixes pentagrammic pyramids into an excavated dodecahedron one obtains the great icosahedron.
If one keeps the center dodecahedron, one get the net of a Dodecahedral pyramid.
Cartesian coordinates
Let be the golden ratio. The 12 points given by and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the points together with the points and cyclic permutations of these coordinates. Multiplying all coordinates of the icosacahedron by a factor of gives a slightly smaller icosahedron. The 12 vertices of this icosahedron, together with the vertices of the dodecahedron, are the vertices of a pentakis dodecahedron centered at the origin. The length of its long edges equals . Its faces are acute isosceles triangles with one angle of and two of . The length ratio between the long and short edges of these triangles equals .
Chemistry
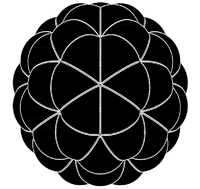
The pentakis dodecahedron in a model of buckminsterfullerene: each surface segment represents a carbon atom. Equivalently, a truncated icosahedron is a model of buckminsterfullerene, with each vertex representing a carbon atom.
Biology
The pentakis dodecahedron is also a model of some icosahedrally symmetric viruses, such as Adeno-associated virus. These have 60 symmetry related capsid proteins, which combine to make the 60 symmetrical faces of a pentakis dodecahedron.
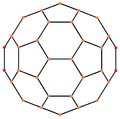
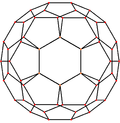
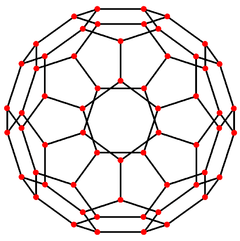
Orthogonal projections
The pentakis dodecahedron has three symmetry positions, two on vertices, and one on a midedge:
| Projective symmetry |
[2] | [6] | [10] |
|---|---|---|---|
| Image |  |
 |
 |
| Dual image |
 |
 |
 |
Related polyhedra

| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||
 |
 |
 |
 |
 |
 |
 |
 |
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||
 |
 |
 |
 |
 |
 | ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
| *n32 symmetry mutation of truncated tilings: n.6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n42 [n,3] |
Spherical | Euclid. | Compact | Parac. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | ||
| Truncated figures |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Config. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| n-kis figures |
 |
 |
 |
 |
 |
 |
 |
|||||
| Config. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
Cultural references
- The Spaceship Earth structure at Walt Disney World's Epcot is a derivative of a pentakis dodecahedron.
- The model for a campus arts workshop designed by Jeffrey Lindsay was actually a hemispherical pentakis dodecahedron https://books.google.com/books?id=JD8EAAAAMBAJ&pg=PA92&dq=jeffrey+lindsay&hl=en&ei=oF88Tv25F7OisQLGwbwt&sa=X&oi=book_result&ct=result&redir_esc=y#v=onepage&q=jeffrey%20lindsay&f=false
- The shape of the "Crystal Dome" used in the popular TV game show The Crystal Maze was based on a pentakis dodecahedron.
- In Doctor Atomic, the shape of the first atomic bomb detonated in New Mexico was a pentakis dodecahedron.
- In De Blob 2 in the Prison Zoo, domes are made up of parts of a Pentakis Dodecahedron. These Domes also appear whenever the player transforms on a dome in the Hypno Ray level.
- Some Geodomes in which people play on are Pentakis Dodecahedra.
References
- Conway, Symmetries of things, p.284
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Sellars, Peter (2005). "Doctor Atomic Libretto". Boosey & Hawkes.
We surround the plutonium core from thirty two points spaced equally around its surface, the thirty-two points are the centers of the twenty triangular faces of an icosahedron interwoven with the twelve pentagonal faces of a dodecahedron.
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR 0730208. (The thirteen semiregular convex polyhedra and their duals, Page 18, Pentakisdodecahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Pentakis dodecahedron )
External links
- Eric W. Weisstein, Pentakis dodecahedron (Catalan solid) at MathWorld.
- Pentakis Dodecahedron – Interactive Polyhedron Model