Closed graph theorem

In mathematics, the closed graph theorem is a basic result which characterizes continuous functions in terms of their graphs. In mathematics, there are several results known as the "closed graph theorem".

The graph of the cubic function f(x) = x³ − 9x on the interval [-4,4] is closed because the function is continuous. The graph of the Heaviside function on [-2,2] is not closed, because the function is not continuous.

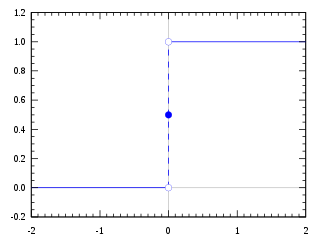
Graphs and maps with closed graphs

If $f:X\to Y$ is a map between topological spaces then the graph of f is the set $\operatorname {Gr} f:=\left\{\left(x,f(x)\right):x\in X\right\}$ or equivalently,

\operatorname {Gr} f:=\lbrace (x,y)\in X\times Y\mid f(x)=y\rbrace .

We say that the graph of f is closed if $\operatorname {Gr} f$ is a closed subset of X × Y (with the product topology).

Any continuous function into a Hausdorff space has a closed graph. However, if X is a non-Hausdorff space then the graph of the identity map $\operatorname {Id} :X\to X$ is the diagonal $\operatorname {Gr} \operatorname {Id} =\{(x,x):x\in X\}$ , which is closed in $X\times X$ if and only if X is Hausdorff.[1]

A function from a compact Hausdorff space into a Hausdorff space is continuous if and only if it has a closed graph.

Closed graph theorem in point-set topology

In point-set topology, the closed graph theorem states the following: If X is a topological space and Y is a compact Hausdorff space, then the graph of T is closed if and only if T is continuous.[2]

For set-valued functions

The closed graph theorem for set-valued functions[3] says that, for a compact Hausdorff range space Y, a set-valued function φ: X→2^Y has a closed graph if and only if it is upper hemicontinuous and φ(x) is a closed set for all x.

In functional analysis

If T is a linear operator between topological vector spaces then we say that T is a closed operator if the graph of T is closed.

The closed graph theorem can be generalized from Banach spaces to more abstract topological vector spaces in the following ways:

A linear operator from a barrelled space X to a Fréchet space Y is continuous if and only if its graph is closed in the space X×Y equipped with the product topology.

and there is a version that does not require Y to be locally convex:[4]

A linear map between two F-spaces is continuous if and only if its graph is closed.[5]

We restate this theorem and extend it with some conditions that can be used to determine if a graph is closed:

If

T:X\to Y

is a linear map between two F-spaces, then the following are equivalent:

T is continuous;
T has a closed graph;
If $\left(x_{i}\right)_{i=1}^{\infty }\to x$ in X and if $\left(T\left(x_{i}\right)\right)_{i=1}^{\infty }$ converges in Y to some $y\in Y$ , then $y=T\left(x\right)$ ;[6]
If $\left(x_{i}\right)_{i=1}^{\infty }\to 0$ in X and if $\left(T\left(x_{i}\right)\right)_{i=1}^{\infty }$ converges in Y to some $y\in Y$ , then $y=0$ .

An even more general version of the closed graph theorem is[7]

Suppose that X and Y are two topological vector spaces (they need not be Hausdorff or locally convex) with the following property: If G is any closed subspace of

X\times Y

and u is any continuous map of G onto X, then u is an open mapping. Under this condition, if

f:X\to Y

is a linear map whose graph is closed then f is continuous.

Between Banach spaces

In functional analysis, the closed graph theorem states the following: If X and Y are Banach spaces, and T : X → Y is a linear operator, then T is continuous if and only if its graph is closed in X × Y (with the product topology).

The closed graph theorem can be reformulated may be rewritten into a form that is more easily usable: If T : X → Y is a linear operator between Banach spaces, then the following are equivalent:

T is continuous.
T is a closed operator (i.e. the graph of T is closed).
If $\left(x_{i}\right)_{i=1}^{\infty }\to x$ in X then $\left(T\left(x_{i}\right)\right)_{i=1}^{\infty }\to T\left(x\right)$ in Y.
If $\left(x_{i}\right)_{i=1}^{\infty }\to 0$ in X then $\left(T\left(x_{i}\right)\right)_{i=1}^{\infty }\to 0$ in Y.
If $\left(x_{i}\right)_{i=1}^{\infty }\to x$ in X and if $\left(T\left(x_{i}\right)\right)_{i=1}^{\infty }$ converges in Y to some $y\in Y$ , then $y=T\left(x\right)$ .
If $\left(x_{i}\right)_{i=1}^{\infty }\to 0$ in X and if $\left(T\left(x_{i}\right)\right)_{i=1}^{\infty }$ converges in Y to some $y\in Y$ , then $y=0$ .

Note that the operator is required to be everywhere-defined, that is, the domain D(T) of T is X. This condition is necessary, as there exist closed linear operators that are unbounded (not continuous); a prototypical example is provided by the derivative operator on C([0,1]), whose domain is a strict subset of C([0,1]).

The usual proof of the closed graph theorem employs the open mapping theorem. In fact, the closed graph theorem, the open mapping theorem and the bounded inverse theorem are all equivalent. This equivalence also serves to demonstrate the importance of X and Y being Banach; one can construct linear maps that have unbounded inverses in this setting, for example, by using either continuous functions with compact support or by using sequences with finitely many non-zero terms along with the supremum norm.

Borel graph theorem

The Borel graph theorem, proved by L. Schwartz, shows that the closed graph theorem is valid for linear maps defined on and valued in most spaces encountered in analysis.[8] Recall that a topological space is called a Polish space if it is a separable complete metrizable space and that a Souslin space is the continuous image of a Polish space. The weak dual of a separable Fréchet space and the strong dual of a separable Fréchet-Montel space are Souslin spaces. Also, the space of distributions and all Lp-spaces over open subsets of Euclidean space as well as many other spaces that occur in analysis are Souslin spaces. The Borel graph theorem states:[9]

Let X and Y be locally convex Hausdorff spaces and let

u:X\to Y

be linear. If X is the inductive limit of an arbitrary family of Banach spaces, if Y is a Souslin space, and if the graph of u is a Borel set in

X\times Y

, then u is continuous.

An improvement upon this theorem, proved by A. Martineau, uses K-analytic spaces. A topological space X is called a $K_{\sigma \delta }$ if it is the countable intersection of countable unions of compact sets. A Hausdorff topological space Y is called K-analytic if it is the continuous image of a $K_{\sigma \delta }$ space (that is, if there is a $K_{\sigma \delta }$ space X and a continuous map of X onto Y). Every compact set is K-analytic so that there are non-separable K-analytic spaces. Also, every Polish, Souslin, and reflexive Frechet space is K-analytic as is the weak dual of a Frechet space. The generalized theorem states:[10]

Let X and Y be locally convex Hausdorff spaces and let

u:X\to Y

be linear. If X is the inductive limit of an arbitrary family of Banach spaces, if Y is a K-analytic space, and if the graph of u is closed in

X\times Y