Absolutely convex set

If S is a subset of a real or complex vector space X, then the following are equivalent:

1. S is a disk;
2. for any scalars a and b satisfying |a| + |b| ≤ 1, aS + bS ⊆ S;
3. for all scalars a, b, and c satisfying |a| + |b| ≤ |c|, aS + bS ⊆ cS;
4. for any scalars a₁, ..., a_n satisfying ${\displaystyle \sum _{i=1}^{n}|a_{i}|\leq 1}$, ${\displaystyle a_{1}S+\cdots +a_{n}S\subseteq S}$;
5. for any scalars c, a₁, ..., a_n satisfying ${\displaystyle \sum _{i=1}^{n}|a_{i}|\leq |c|}$, ${\displaystyle a_{1}S+\cdots +a_{n}S\subseteq cS}$;

The intersection of arbitrarily many absolutely convex sets is again absolutely convex; however, unions of absolutely convex sets need not be absolutely convex anymore.

The disked hull of a set is equal to the convex hull of the balanced hull of that set; it is also equal to the intersection of all disks containing that set.

If D is an absorbing disk in a vector space X then there exists an absorbing disk E in X such that E + E ⊆ D.[1]

The light gray area is the absolutely convex hull of the cross.

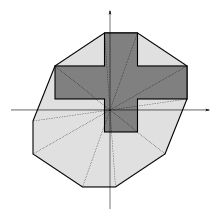
Let X be a real or complex vector space. The smallest convex (resp. balanced) subset of X containing a set is called the convex hull (resp. balanced hull) of that set and is denoted by co(S) (resp. bal(S)). For any subset S of X, the convex balanced hull of S (also called the absolute convex hull, or the disked hull), denoted by cobal(S), is the smallest subset of X containing S that is convex and balanced.[2] The convex balanced hull of a set S the intersection of all absolutely convex sets containing S, analogous to the well-known construction of the convex hull. More explicitly, one can define the absolutely convex hull of the set A via ${\displaystyle {\mbox{cobal}}(A)=\left\{\sum _{i=1}^{n}\lambda _{i}x_{i}:n\in \mathbb {N} ,\,x_{i}\in A,\,\sum _{i=1}^{n}|\lambda _{i}|\leq 1\right\},}$ where the λ_i are elements of the underlying field. The convex balanced hull of S is equal to the convex hull of the balanced hull of S, that is, cobal(S) = co(bal(S)).

The convex balanced hull of S contains both the convex hull of S and the balanced hull of S. The absolutely convex hull of a bounded set in a topological vector space is again bounded.

The Wikibook Algebra has a page on the topic of: Vector spaces

• Balanced set
• Convex set
• Vector (geometric), for vectors in physics
• Vector field

• Robertson, A.P.; W.J. Robertson (1964). Topological vector spaces. Cambridge Tracts in Mathematics. 53. Cambridge University Press. pp. 4–6.
• Narici, Lawrence; Beckenstein, Edward (July 26, 2010). Topological Vector Spaces, Second Edition. Pure and Applied Mathematics (Second ed.). Chapman and Hall/CRC.

• Schaefer, H.H. (1999). Topological vector spaces. Springer-Verlag Press. p. 39.