Julia sets for polynomial functions

The elephants zone in z^2+z^3+c fractal

" The dynamics of polynomials is much better understood than the dynamics of general rational maps" due to the Bottcher’s theorem^[1]

"the mulitbrot family, ... they all have a single critical point, namely the origin" ^[2] Mark McClure )

z(1 + z)^d

Map $z(1+z)^{d}$ has d petals. "Although the parabolic point at z = 0 has only one petal, the map f also has a preparabolic critical point b = −1 of local degree d. Thus f has d petals at b. " ^[3]

For exmple "the filled Julia set of f (z) = z(1 + z) 3 has three petals at z = −1." ( Curtis T McMullen )

mz(1+z^(k*n))

"The condition

  $z^{kn}\in R$

describes a set of lines through the origin. Note that the map g

  $g(z)=z(1+z^{kn})$

leaves these lines invariant. Then

  $z\to \lambda *z(1+z^{kn})$

is the composition of g with the periodic rotation "^[4]

  $z\to \lambda z$

z(1-z^q)

z^n+ z + c

Example ^[5]

f (z) = z^3 + z + 0.6*I

z^n + c^p

Z = Zⁿ + c^p

L = (m - 1) * p

Z = Z² + C²
L = (2 - 1)* 2 = 2
Z = Z² + C³
L = (2 - 1)* 3 = 3
Z = Z²+C⁶ - 1
L = (2 - 1)* 6 = 6
Z = Z³ + C²
L = (3 - 1)* 2 = 4
Z = Z³ + C³
L = (3 - 1)* 3 = 6
Z = Z⁴ + C⁴
L = (4 - 1)* 4 = 12

z^n + c

Multibrot sets ^[6]^[7]^[8]^[9]

L = m - 1

Compare with it's inverse parameter plane : Z^n + 1/c ^[10]

How to compute powers of z :

 $Z^{2}=(x+iy)^{2}$   $\mathrm {Real} =x^{2}-y^{2}$    $\mathrm {Imag} =2xy$

 $Z^{3}=(x+iy)^{3}$   $\mathrm {Real} =x^{3}-3y^{2}x$    $\mathrm {Imag} =3x^{2}y-y^{3}$

 $Z^{4}=(x+iy)^{4}$   $\mathrm {Real} =x^{4}-6x^{2}y^{2}+y^{4}$    $\mathrm {Imag} =4x^{3}y-4xy^{3}$

 $Z^{5}=(x+iy)^{5}$   $\mathrm {Real} =x^{5}-10x^{3}y^{2}+5xy^{4}$    $\mathrm {Imag} =5x^{4}y-10x^{2}y^{3}+y^{5}$

 $Z^{6}=(x+iy)^{6}$   $\mathrm {Real} =x^{6}-15x^{4}y^{2}+15x^{2}y^{4}-y^{6}$    $\mathrm {Imag} =6x^{5}y-20x^{3}y^{3}+6xy^{5}$

 $Z^{7}=(x+iy)^{7}$   $\mathrm {Real} =x^{7}-21x^{5}y^{2}+35x^{3}y^{4}-7xy^{6}$    $\mathrm {Imag} =7x^{6}y-35x^{4}y^{3}+21x^{2}y^{5}-y^{7}$

Fortan source code :

! Fortran program by P.M.J. Trevelyan
! http://philiptrevelyan.co.uk/
     PROGRAM FRACTAL
      IMPLICIT NONE
      INTEGER I,J,ITERATION,N,M
      PARAMETER(N=2000,M=50)
      REAL*8 U,V,X,Y,P,Q
      OPEN(99,FILE='Fractal_quad.dat')
 25   FORMAT(2F9.5,I3)
      DO 10, I=1,N
      DO 20, J=1,N
C Define first point z(n)=U+iV and k=X+iY
      U=0.D0
      V=0.D0
      X=I*3.2D0/(N-1.D0)-2.1D0
      Y=J*2.8D0/(N-1.D0)-1.4D0
      DO 30, ITERATION=1,M
C Calculate z(n+1) = z(n)**2 + k where z(n+1)=P+iQ
      P=U**2-V**2+X 
      Q=2.D0*U*V+Y
      U=P
      V=Q
C If |z|>2 stop iterating
      If (U**2+V**2.GT.4.D0) GOTO 100
 30       CONTINUE
 100      WRITE(99,25) X,Y,ITERATION
 20     CONTINUE
 10   CONTINUE
      STOP
      END

Parameter planes for positive integer powers :

z² + c
z³ + c
z⁴ + c
z⁵ + c
z⁶ + c

Negative powers

When d is negative the set surrounds but does not include the origin. There is interesting complex behaviour in the contours between the set and the origin, in a star-shaped area with (1 − d)-fold rotational symmetry. The sets appear to have a circular perimeter, however this is just an artifact of the fixed maximum radius allowed by the Escape Time algorithm, and is not a limit of the sets that actually extend in all directions to infinity.

z⁻² + c
z⁻³ + c
z⁻⁴ + c
z⁻⁵ + c
z⁻⁶ + c

z^2+c

See complex quadratic polynomials

z^3 + c

$z_{n+1}=z_{n}^{3}+c$

It can be computed by :^[11]

$X_{n+1}=X_{n}^{3}-3X_{n}Y_{n}^{2}+C_{x}$

$Y_{n+1}=3X_{n}^{2}Y_{n}-Y_{n}^{3}+C_{y}$

Examples:

c= -0.040000000000000036 + I * -0.78^[12]

Parameter plane and Mandelbrot set
Dynamic plane and Julia set for $f(z)=z^{3}+c$ where c = ?
zeros of the function $z^{3}-1$ in the complex plane
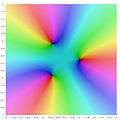complex color plot of the function $z^{3}-1$ in the complex plane
c = -0.4730679 -0.5625i

z^5 + c

Parameter plane and Mandelbrot set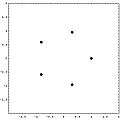
zeros of the function $z^{5}-1$ in the complex plane
complex color plot of the function $z^{5}-1$ in the complex plane

z^10 + c

Julia Set fractal using z = z^10 + c where c = -0.925 + 0.19i

zⁿ + 1/c

It is an inverted parameter plain of z^n + c.

Number of vertices : V = (n - 1)

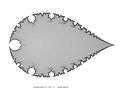
Z = Z² + 1/C
Z = Z³ + 1/C
Z = Z⁴ + 1/C
Z = Z⁵ + 1/C
Z = Z⁶ + 1/C
Z = Z⁷ + 1/C

z^n + m*z^(-d)

McMullen maps :

$z^{n}+{\frac {m}{z^{d}}}$

where : z and d are >=1

"These maps are known as `McMullen maps', since McMullen ^[13] first studied these maps and pointed out that when (n;m) = (2; 3) and m is small, the Julia set is a Cantor set of circles." ^[14]

z^n + m*z

Description ^[15]^[16]

z^2+m*z

See complex quadratic polynomial

z^3+m*z

dynamic planes

z^3 + z

It can be found using Maxima CAS :

(%i2) z:zx+zy*%i;
(%o2) %i*zy+zx
(%i6) realpart(z+z^3);
(%o6) -3*zx*zy^2+zx^3+zx
(%i7) imagpart(z+z^3);
(%o7) -zy^3+3*zx^2*zy+zy

Finding roots and its multiplicity :

z^{3}+z=z

z^{3}=0

so root z=0 has multiplicity 3.

(%i1) z1:z^3+z;
(%o1) z^3+z
(%i2) solve(z1=z);
(%o2) [z=0]
(%i3) multiplicities;
(%o3) [3]

It means that there is a flower with 2 petals around fixed point z=0.

Compare figures :

by Alessandro Rosa^[17]
by Xavier Buff and Adam L. Epstein^[18]

z^4 + mz

How to compute iteration :

(%i1) z:zx+zy*%i;
(%o1) %i*zy+zx
(%i2) m:mx+my*%i;
(%o2) %i*my+mx
(%i3) z1:z^4+m*z;
(%o3) (%i*zy+zx)^4+(%i*my+mx)*(%i*zy+zx)
(%i4) realpart(z1);
(%o4) zy^4-6*zx^2*zy^2-my*zy+zx^4+mx*zx
(%i5) imagpart(z1);
(%o5) -4*zx*zy^3+4*zx^3*zy+mx*zy+my*zx

See also f(z) = c(z^4-4z). It is a family 4.1 in program Mandel by Wolf Jung^[19] ( see main menu / New / 4. Quartic polynomials / 4.1 )

Here c = -m/4 and Mandelbrot set is rotated by 180 degrees.

Parameter plane

Parameter plane and Mandelbrot set for f(z) = z^4 + m*z

Period 1 components

Maxima CAS code :

(%i1) f:z^4+m*z;
(%o1) z^4+m*z
(%i2) e1:f=z;
(%o2) z^4+m*z=z
(%i3) d:diff(f,z,1);
(%o3) 4*z^3+m
(%i4) e2:d=w;
(%o4) 4*z^3+m=w
(%i5) s:eliminate ([e1,e2], [z]);
(%o5) [-(m-w)*(w+3*m-4)^3]
(%i6) s:solve([s[1]], [m]);
(%o6) [m=-(w-4)/3,m=w]

It means that there are 2 period 1 components :

one with radius = 1 and center =0 ( m=w )
second with radius 1/3 and center=4/3 ( m=-(w-4)/3 )

Dynamic planes

z^4+z

Julia set for f(z) = z^4 + z

Finding roots and its multiplicity :

z^{4}+z=z

z^{4}=0

so root z=0 has multiplicity 4.

(%i1) z1:z^4+z;
(%o1) z^4+z
(%i2) solve(z1=z);
(%o2) [z=0]
(%i3) multiplicities;
(%o3) [4]

It means that there are 3 petals around fixed point z=0 ^[20]

How to compute iteration :

(%i17) z:x+y*%i;
(%o17) %i*y+x
(%i18) realpart(z+z^4);
(%o18) y^4-6*x^2*y^2+x^4+x
(%i19) imagpart(z+z^4);
(%o19) -4*x*y^3+4*x^3*y+y

z^4-iz

Critical orbits for f(z)=z^4-iz

First compute multiplier for internal angle=3/4 :

(%i1) m:exp(2*%pi*%i*3/4);
(%o1) -%i

Then find how to compute iteration :

(%i1) z:x+y*%i;
(%o1) %i*y+x
(%i2) z1:z^4-%i*z;
(%o2) (%i*y+x)^4-%i*(%i*y+x)
(%i3) realpart(z1);
(%o3) y^4-6*x^2*y^2+y+x^4
(%i4) imagpart(z1);
(%o4) -4*x*y^3+4*x^3*y-x

It is a parabolic Julia set with 12 petal flower ^[21]

Critical points :

(%i12) s:GiveListOfCriticalPoints(f(z))
(%o12) [0.31498026247372*%i-0.54556181798586,-0.62996052494744*%i,0.31498026247372*%i+0.54556181798586]
(%i13) multiplicities
(%o13) [1,1,1]
(%i14) length(s)
(%o14) 3

with arguments in turns :

[0.41666666666667,0.75,0.083333333333334] = [5/12 , 9/12, 1/12]

Attracting vectors

Multiplier of fixed point −i is a fourth root of unity ( q=4), thus we examine 4-th iteration :

(%i1) z1:z^4-%i*z;
(%o1) z^4-%i*z
(%i2) z2:z1^4-%i*z1;
(%o2) (z^4-%i*z)^4-%i*(z^4-%i*z)
(%i3) z3:z2^4-%i*z2;
(%o3) ((z^4-%i*z)^4-%i*(z^4-%i*z))^4-%i*((z^4-%i*z)^4-%i*(z^4-%i*z))
(%i4) z4:z3^4-%i*z3;
(%o4) (((z^4-%i*z)^4-%i*(z^4-%i*z))^4-%i*((z^4-%i*z)^4-%i*(z^4-%i*z)))^4-%i*(((z^4-%i*z)^4-%i*(z^4-%i*z))^4-%i*((z^4-%i*z)^4-%i*(z^4-%i*z)))
(%i6) taylor(z4,z,0,20);
(%o6)/T/ z+(-76*%i-84)*z^13+(-36*%i+720)*z^16+(1812*%i-2556)*z^19+...

Next term after z is a :

(-76*%i-84)*z^13

so here :

k=13 and n=m*q = k-1 = 12
a = -76*%i-84

Attracting vectors satisfy :

$nav^{n}=-1$

so here :

$-12(76i+84)v^{12}=-1$

$v^{12}={\frac {1}{912i+1008}}$

One can solve it in Maxima CAS :

(%i14) s:map('float,s);
(%o14) [1.007236559448514*%i+1.521106958434882,1.632845927320289*%i+0.81369898815363,
1.820935547602145*%i-0.11173896888541,1.521106958434882*%i-1.007236559448514,
0.81369898815363*%i-1.632845927320289,
-0.11173896888541*%i-1.820935547602145,-1.007236559448514*%i-1.521106958434882,
-1.632845927320289*%i-0.81369898815363,0.11173896888541-1.820935547602145*%i,
1.007236559448514-1.521106958434882*%i,
1.632845927320289-0.81369898815363*%i,0.11173896888541*%i+1.820935547602145]

With arguments in turns :

[0.093087406197659,0.17642073953099,0.25975407286433,0.34308740619766,0.42642073953099,0.50975407286433,
0.59308740619766,0.67642073953099,0.75975407286433,0.84308740619766,0.92642073953099,0.009754072864326]

different then arguments of critical points. Thus critical orbits form distorted 12-arms star

Find the fixed points :

(%i1) f:z^4-%i*z;
(%o1) z^4-%i*z
(%i2) s:solve(f=z);
(%o2) [z=((%i+1)^(1/3)*(sqrt(3)*%i-1))/2,z=-((%i+1)^(1/3)*(sqrt(3)*%i+1))/2,z=(%i+1)^(1/3),z=0]
(%i4) multiplicities;
(%o4) [1,1,1,1]
(%i3) s:map(rhs,s);
(%o3) [((%i+1)^(1/3)*(sqrt(3)*%i-1))/2,-((%i+1)^(1/3)*(sqrt(3)*%i+1))/2,(%i+1)^(1/3),0]
(%i5) s:map('float,s);
(%o5) [0.5*(%i+1.0)^(1/3)*(1.732050807568877*%i-1.0),-0.5*(%i+1.0)^(1/3)*(1.732050807568877*%i+1.0),(%i+1.0)^(1/3),0.0]
(%i6) s:map(rectform,s);
(%o6) [0.7937005259841*%i-0.7937005259841,-1.084215081491351*%i-0.29051455550725,0.29051455550725*%i+1.084215081491351,0.0]

Compute the multiplier of fixed points :

(%i7) d:diff(f,z,1);
(%o7) 4*z^3-%i

Check the stability of fixed points :

(%i9) for z in s do disp(abs(ev(d)));
4.999999999999998
5.0
4.999999999999999
1
(%o9) done

Point z=0 is a parabolic point.

z^4 -z

Critical points, orbits for f(z) = z^4 - z

Julia set for f(z) = z^4 - z

Julia set for f(z) = z^4 - z with various number of star branches ( animation ) - repelling petals

It is a special case of polynomial from family :

$f_{\lambda }(z)=z^{4}+\lambda z$

Here

$\lambda =-1=e^{\pi i}$

so internal angle $\theta$ is :

$\theta ={\frac {p}{q}}={\frac {1}{2}}$

(%i2) m:exp(2*%pi*%i/2);
(%o2) -1

Because :

$|\lambda |=1$

it is a parabolic Julia set. Point $\lambda =-1=e^{\pi i}$ is between two period one components ( root point ).

Periodic points

Point z=0 is a root of multiplicity seven

$k=m*q+1=3*2+1=7$

for equation :

$f_{\lambda }^{2}(z)=z$

One can check it in Maxima CAS using numerical :

(%i1) z1:z^4-z;
(%o1) z^4-z
(%i2) z2:z1^4-z1;
(%o2) (z^4-z)^4-z^4+z
(%i3) eq2:z2-z=0;
(%o3) (z^4-z)^4-z^4=0
(%i4) allroots(eq2);
(%o4) [z=0.0,z=0.0,z=0.0,z=0.0,z=0.0,z=0.0,z=0.0,z=1.259921049894873,
z=0.7937005259841*%i-0.7937005259841,z=-0.7937005259841*%i-0.7937005259841,
z=1.084215081491351*%i-0.29051455550725,z=-1.084215081491351*%i-0.29051455550725,
z=0.29051455550725*%i+1.084215081491351,
z=1.084215081491351-0.29051455550725*%i,z=1.091123635971722*%i-0.62996052494744,
z=-1.091123635971722*%i-0.62996052494744]
(%i5) expand(eq2);
(%o5) z^16-4*z^13+6*z^10-4*z^7=0
(%i6) factor(eq2);
(%o6) z^7*(z^3-2)*(z^6-2*z^3+2)=0

and symbolic methods :

(%i1) z1:z^4-z;
(%o1) z^4-z
(%i2) solve(z1=z);
(%o2) [z=(2^(1/3)*sqrt(3)*%i-2^(1/3))/2,z=-(2^(1/3)*sqrt(3)*%i+2^(1/3))/2,z=2^(1/3),z=0]
(%i3) multiplicities;
(%o3) [1,1,1,1]
(%i4) z2:z1^4-z1;
(%o4) (z^4-z)^4-z^4+z
(%i5) solve(z2=z);
(%o5) [z=(2^(1/3)*sqrt(3)*%i-2^(1/3))/2,z=-(2^(1/3)*sqrt(3)*%i+2^(1/3))/2,z=2^(1/3),z=((%i+1)^(1/3)*(sqrt(3)*%i-1))/2,z=-((%i+1)^(1/3)*(sqrt(3)*%i+1))/2,z=(%i+1)^(1/3),z=(sqrt(3)*(1-%i)^(1/3)*%i-(1-%i)^(1/3))/2,z=-(sqrt(3)*(1-%i)^(1/3)*%i+(1-%i)^(1/3))/2,z=(1-%i)^(1/3),z=0]
(%i6) multiplicities;
(%o6) [1,1,1,1,1,1,1,1,1,7]

Number of petals = 6 ^[22]

$m*q=3*2=6$

Atracting vectors Denominator of internal angle $\theta ={\frac {p}{q}}={\frac {1}{2}}$ is $q=2$ so one have to check second iteration of function :

(%i5) z1:z^4-z;
(%o5) z^4-z
(%i6) z2:z1^4-z1;
(%o6) (z^4-z)^4-z^4+z
(%i8) expand(z2);
(%o8) z^16-4*z^13+6*z^10-4*z^7+z

Next term after z is a -4z^7. Then :

k = 7 and n=m*q = k-1 = 6
a = -4

Attracting vectors satisfy :

$nav^{n}=-1$

so here :

$-24v^{6}=-1$

$v^{6}={\frac {1}{24}}$

One can solve it using Maxima CAS :

(%i10) s:solve(z^6=1/24);
(%o10) [z=(sqrt(3)*%i+1)/(2^(3/2)*3^(1/6)),z=(sqrt(3)*%i-1)/(2^(3/2)*3^(1/6)),z=-1/(sqrt(2)*3^(1/6)),z=-(sqrt(3)*%i+1)/(2^(3/2)*3^(1/6)),z=-(sqrt(3)*%i-1)/(2^(3/2)*3^(1/6)),z=1/(sqrt(2)*3^(1/6))]
(%i11) s:map(rhs,s);
(%o11) [(sqrt(3)*%i+1)/(2^(3/2)*3^(1/6)),(sqrt(3)*%i-1)/(2^(3/2)*3^(1/6)),-1/(sqrt(2)*3^(1/6)),-(sqrt(3)*%i+1)/(2^(3/2)*3^(1/6)),-(sqrt(3)*%i-1)/(2^(3/2)*3^(1/6)),1/(sqrt(2)*3^(1/6))]
(%i12) s:map('float,s);
(%o12) [0.29439796075012*(1.732050807568877*%i+1.0),0.29439796075012*(1.732050807568877*%i-1.0),-0.58879592150024,-0.29439796075012*(1.732050807568877*%i+1.0),-0.29439796075012*(1.732050807568877*%i-1.0),0.58879592150024]
(%i13) s:map(rectform,s);
(%o13) [0.50991222566388*%i+0.29439796075012,0.50991222566388*%i-0.29439796075012,-0.58879592150024,-0.50991222566388*%i-0.29439796075012,0.29439796075012-0.50991222566388*%i,0.58879592150024]
(%i14) s:map(carg_t,s);
(%o14) [0.5235987755983/%pi,1.047197551196598/%pi,1/2,1-1.047197551196598/%pi,1-0.5235987755983/%pi,0]
(%i15) s:map('float,s);
(%o15) [0.16666666666667,0.33333333333333,0.5,0.66666666666667,0.83333333333333,0.0]

So critical points lie on attracting vectors. Thus critical orbits tend straight to the origin under the iteration^[23]

How to compute $f_{\lambda }(z)$ :

(%i2) z:x+y*%i;
(%o2) %i*y+x
(%i3) realpart(z^4-z);
(%o3) y^4-6*x^2*y^2+x^4-x
(%i4) imagpart(z^4-z);
(%o4) -4*x*y^3+4*x^3*y-y

Critical points :

s:GiveListOfCriticalPoints(f(z))
(%o8) [0.54556181798586*%i-0.31498026247372,-0.54556181798586*%i-0.31498026247372,0.62996052494744]

These points has arguments in turns : 1/3, 2/3, 0

z^5 + m*z

dynamic planes

z^5 + z

Julia set z+z^5. Image and src code

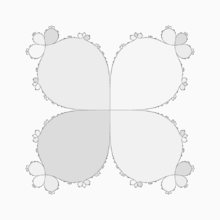
Finding roots and its multiplicity :

z^{5}+z=z

z^{5}=0

so root z=0 has multiplicity 5. It means that there is a flower with 4 petals ^[24]

around fixed point z=0.

It How to compute :

(%i23)  z:x+y*%i;
(%o23) %i*y+x
(%i24) realpart(z+z^5);
(%o24) 5*x*y^4-10*x^3*y^2+x^5+x
(%i25) imagpart(z+z^5);
(%o25) y^5-10*x^2*y^3+5*x^4*y+y

In c programs one must use temporary variable so it can be :

tempx = 5*x*y*y*y*y-10*x*x*x*y*y + x*x*x*x*x + x ; // temporary variable
y = y*y*y*y*y -10*x*x*y*y*y + 5*x*x*x*x*y + y ;
x=tempx;

It can be optimized

"...an escape time algorithm would take forever to generate that type of image, since the dynamics are so slow there. If you want resolution of 1/100, it would take roughly 2*10^8 iterates to move the point z0=0.01 to z=2 by iterating f(z)=z+z^5." ( Mark McClure ^[25]

"This picture shows the Julia Set of f(z) = z + z^5 which has an indifferent fixed point at z = 0. ( f(0) = 0 and f ' (0) = 1 .)

The 4 lines :

Re z = 0 and Im z = 0 and Re z = Im z and Re z = -Im z

are invariant under iteration of f.

On Im z = 0: f(x) = x + x^5

On Re z = 0: f(ix) = ix + (ix)^5 = ix + i^5 x^5 = i(x+x^5)

On Re z = Im z , f(z) = r e^(i pi/4) + r^5 e^(i 5 pi/4) = e^ (i pi/4)(r - r^5)

On Re z = -Im z, f(z) = = r e^(i 3pi/4) + r^5 e^(i 15 pi/4) = e^ (i 3pi/4)(r - r^5)

Using one dimensional analysis it is easily shown that f(x) = x + x^5 has a repelling fixed point at x = 0 and f(x) = x - x^5 has an attracting fixed point at x = 0. Thus along the four invariant lines 0 is attracting on the first two and repelling on the second two. The points repelled from 0 are shown in shades of blue, while those attracted to 0 are shown in shades of brown. 0 has four attracting petals, which are in shades of brown. (A simply connected region C is a petal for an indifferent fixed point p if p is contained in the boundary of C and for each z in C,

F^n(z) -> p (see Devaney - 1987)" ^[26]

z^6+m*z

dynamical plane

z6+z on plane [-1.2;1.2]x[-1.2;1.2]. It has 5 petals ^[27]

z^14 + m*z

dynamic plane

z^14 - z

Julia set for f(z) = z^14 - z . Image and c src code

Critical orbit for f(z) = z^14 - z . Image and Maxima CAS src code

How to compute iteration :

/* Maxima CAS session */
(%i1) z:x+y*%i;
(%o1) %i*y+x
(%i2) z1:z^14-z;
(%o2) (%i*y+x)^14-%i*y-x
(%i3) realpart(z1);
(%o3) -y^14+91*x^2*y^12-1001*x^4*y^10+3003*x^6*y^8-3003*x^8*y^6+1001*x^10*y^4-91*x^12*y^2+x^14-x
(%i4) imagpart(z1);
(%o4) 14*x*y^13-364*x^3*y^11+2002*x^5*y^9-3432*x^7*y^7+2002*x^9*y^5-364*x^11*y^3+14*x^13*y-y

f(z)=z^14-z, on [-1,2;1,2]x[-1,2;1,2] has 26 petals. Compare with image by Michael Becker.^[28]

How to find fixed points :

(%i1) z1:z^14-z;
(%o1) z^14-z
(%i2) solve(z1=z);
(%o2) [z=2^(1/13)*%e^((2*%i*%pi)/13),z=2^(1/13)*%e^((4*%i*%pi)/13),
     z=2^(1/13)*%e^((6*%i*%pi)/13),z=2^(1/13)*%e^((8*%i*%pi)/13),
     z=2^(1/13)*%e^((10*%i*%pi)/13),z=2^(1/13)*%e^((12*%i*%pi)/13),
     z=2^(1/13)*%e^(-(12*%i*%pi)/13),z=2^(1/13)*%e^(-(10*%i*%pi)/13),
     z=2^(1/13)*%e^(-(8*%i*%pi)/13),z=2^(1/13)*%e^(-(6*%i*%pi)/13),
     z=2^(1/13)*%e^(-(4*%i*%pi)/13),z=2^(1/13)*%e^(-(2*%i*%pi)/13),
     z=2^(1/13),z=0]
(%i3) multiplicities;
(%o3) [1,1,1,1,1,1,1,1,1,1,1,1,1,1]
(%i4) z2:z1^14-z1;
(%o4) (z^14-z)^14-z^14+z
(%i5) solve(z2=z);
(%o5) [z=2^(1/13)*%e^((2*%i*%pi)/13),z=2^(1/13)*%e^((4*%i*%pi)/13),
   z=2^(1/13)*%e^((6*%i*%pi)/13),z=2^(1/13)*%e^((8*%i*%pi)/13),
   z=2^(1/13)*%e^((10*%i*%pi)/13),z=2^(1/13)*%e^((12*%i*%pi)/13),
   z=2^(1/13)*%e^(-(12*%i*%pi)/13),z=2^(1/13)*%e^(-(10*%i*%pi)/13),
   z=2^(1/13)*%e^(-(8*%i*%pi)/13),z=2^(1/13)*%e^(-(6*%i*%pi)/13),
   z=2^(1/13)*%e^(-(4*%i*%pi)/13),z=2^(1/13)*%e^(-(2*%i*%pi)/13),
   z=2^(1/13),z=0,0=z^78-7*z^65+21*z^52-35*z^39+35*z^26-21*z^13+7,
   0=z^78-5*z^65+11*z^52-13*z^39+9*z^26-3*z^13+1]
(%i6) multiplicities;
(%o6) [1,1,1,1,1,1,1,1,1,1,1,1,1,27,1,1]

z^15 +m*z

dynamic plane

z^15-z

Julia set for f(z)= z^15-z

Critical points and orbits for f(z)= z^15-z

How to compute iterations :

/* Maxima CAS session */
(%i1) z:x+y*%i;
(%o1) %i*y+x
(%i2) z1:z^15-z;
(%o2) (%i*y+x)^15-%i*y-x
(%i3) realpart(z1);
(%o3) -15*x*y^14+455*x^3*y^12-3003*x^5*y^10+6435*x^7*y^8-5005*x^9*y^6+1365*x^11*y^4-105*x^13*y^2+x^15-x
(%i4) imagpart(z1);
(%o4) -y^15+105*x^2*y^13-1365*x^4*y^11+5005*x^6*y^9-6435*x^8*y^7+3003*x^10*y^5-455*x^12*y^3+15*x^14*y-y

Critical points :

(%i1) m:-1;
f:z^15+ m*z;
d:diff(f,z,1);
s:solve(d=0,z)$
s:map(rhs,s)$
s:map(rectform,s)$
s:map('float,s);
multiplicities;
(%o1) -1
(%o2) z^15-z
(%o3) 15*z^14-1
(%o7) 
[0.35757475986465*%i+0.74251163973317,
0.64432745317147*%i+0.51383399763062,
0.80346319222004*%i+0.1833852305369,
0.80346319222004*%i-0.1833852305369,
0.64432745317147*%i-0.51383399763062,
0.35757475986465*%i-0.74251163973317,
-0.8241257452789,
-0.35757475986465*%i-0.74251163973317,
-0.64432745317147*%i-0.51383399763062,
-0.80346319222004*%i-0.1833852305369,
0.1833852305369-0.80346319222004*%i,
0.51383399763062-0.64432745317147*%i,
0.74251163973317-0.35757475986465*%i,
0.8241257452789]
(%o8) [1,1,1,1,1,1,1,1,1,1,1,1,1,1]

It means that here are 14 critical points and 14 critical orbits.

Fixed points :

kill(all);
remvalue(all);

/*------------- functions definitions ---------*/

/* function */
f(z):=z^15 -z;

/* find fixed points  returns a list */
GiveFixedPoints():= block
(
  [s],
  s:solve(f(z)=z),
  /* remove "z="  from list s */
  s:map('rhs,s),
  s:map('rectform,s),
  s:map('float,s),
  return(s)
)$

compile(all);

ff:GiveFixedPoints();
multiplicities;
length(s);

for i:1 thru length(ff) step 1 do
  (z:ff[i],
   disp("z= ",z, " abs(d(z))= ",abs(15*z^14-1)));

Result is :

(%i12) ff:GiveFixedPoints()
(%o12) [0.45590621928146*%i+0.94669901916834,0.82151462051137*%i+0.65513604843564,1.024411975933374*%i+0.23381534859391,
1.024411975933374*%i-0.23381534859391,0.82151462051137*%i-0.65513604843564,0.45590621928146*%i-0.94669901916834,-1.050756638653219,-
0.45590621928146*%i-0.94669901916834,-0.82151462051137*%i-0.65513604843564,-1.024411975933374*%i-0.23381534859391,0.23381534859391-
1.024411975933374*%i,0.65513604843564-0.82151462051137*%i,0.94669901916834-0.45590621928146*%i,1.050756638653219,0.0]
(%i13) multiplicities
(%o13) [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
(%i14) length(s)
(%o14) 14
(%i15) for i thru length(ff) do (z:ff[i],disp("z= ",z," abs(d(z))= ",abs(15*z^14-1)))
z= 0.45590621928146*%i+0.94669901916834 ; abs(d(z))= 28.99999999999996
z= 0.82151462051137*%i+0.65513604843564 ; abs(d(z))= 28.99999999999998
z= 1.024411975933374*%i+0.23381534859391 ; abs(d(z))= 28.99999999999999
z= 1.024411975933374*%i-0.23381534859391 ; abs(d(z))=  28.99999999999997
z= 0.82151462051137*%i-0.65513604843564 ; abs(d(z))= 29.00000000000001
z= 0.45590621928146*%i-0.94669901916834 ; abs(d(z))=  28.99999999999995
z= -1.050756638653219 ;                   abs(d(z))= 29.00000000000003
z=  -0.45590621928146*%i-0.94669901916834; abs(d(z))= 28.99999999999995
z= -0.82151462051137*%i-0.65513604843564; abs(d(z))=  29.00000000000001
z= -1.024411975933374*%i-0.23381534859391 ; abs(d(z))= 28.99999999999997
z= 0.23381534859391-1.024411975933374*%i abs(d(z))= 28.99999999999999
z= 0.65513604843564-0.82151462051137*%i ; abs(d(z))= 28.99999999999998
z= 0.94669901916834-0.45590621928146*%i ; abs(d(z))=  28.99999999999996
z= 1.050756638653219 ;                    abs(d(z))= 29.00000000000003
z= 0.0 ;                                   abs(d(z))= 1.0

So only z=0 is parabolic fixed points, the rest of them are repelling

Other

z^5+m*z^4+z

Parabolic Julia set for f(z)=z^5+m*z^4+z where m = 0.8+0.4*i

Inside dynamics under generalized power setting

The orbit dynamics of the set can become more complex when the power is something other than 2.0. The iterated function can become multivalued and the structure of the set is then affected by the 'arbitrary' choice of which value is chosen.

References

↑ ON THE NOTIONS OF MATING by CARSTEN LUNDE PETERSEN AND DANIEL MEYER
↑ Mark McClure - comment
↑ dimension and conformal dynamics II: Geometrically finite rational maps by Curtis T McMullen
↑ COMPLEX ANALYTIC DYNAMICS ON THE RIEMANN SPHERE BY PAUL BLANCHARD
↑ Inverse Iteration Algorithms for Julia Sets by Mark McClure
↑ wikipedia : Multibrot_set
↑ High-Order Mandelbrot and Julia Sets Written by Christopher Thomas. Images and Perl program
↑ Stephen Haas : The Hausdorff Dimension of the Julia Set of Polynomials of the Form z^d+c
↑ video on youtube by rrwick
↑ Desenvolupament_de_fractals_mitjan
↑ De la génération des fractales Théorie et Applications John Bonobo
↑ wolfram : julia-set-explorations
↑ C. McMullen, Automorphisms of rational maps. In `Holomorphic Functions and Moduli I', 31-60, Springer-Verlag, 1988.
↑ Hyperbolic components of McMullen maps Weiyuan Qiu, Pascale Roesch, Xiaoguang Wang, Yongcheng Yin
↑ "Visualizing the complex dynamics of families of polynomials with symmetric critical points" by Ning Chena, Jing Suna, Yan-ling Suna, Ming Tangb. Chaos, Solitons & Fractals. Volume 42, Issue 3, 15 November 2009, Pages 1611–1622
↑ A topological characterisation of holomorphic parabolic germs in the plane Fr ́ed ́eric Le Roux
↑ One approach to the digital visualization of hedgehogs in holomorphic dynamics Alessandro Rosa, fig 5.13 page 26
↑ A parabolic Pommerenke-Levin-Yoccoz inequality by Xavier Buff and Adam L. Epstein, fig 1 page 4
↑ Mandel: software for real and complex dynamics by Wolf Jung
↑ Complex dynamics, Lennart Carleson, Theodore W. Gamelin, Springer, 1993, ISBN 978-0-387-97942-7. Page 40, Figure 2.
↑ F. Bracci, Local holomorphic dynamics of diffeomorphisms in dimension one. Contemporary Mathematics 525, (2010), 1-42. Notes of the PhD course given in A.A 2007/08.
↑ Complex dynamics, Lennart Carleson, Theodore W. Gamelin, Springer, 1993, ISBN 978-0-387-97942-7. Page 41
↑ Mark McClure in stackexchange questions : what-is-the-shape-of-parabolic-critical-orbit
↑ One approach to the digital visualization of hedgehogs in holomorphic dynamics Alessandro Rosa
↑ stackexchange questions : what-is-the-shape-of-parabolic-critical-orbit
↑ Fractals by Anne Burns, Department of Mathematics, C.W. Post Campus, Long Island University
↑ Some Julia sets 2 by Michael Becker
↑ Fixpunkte und Periodische Punkte by Michael Becker

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] ON THE NOTIONS OF MATING by CARSTEN LUNDE PETERSEN AND DANIEL MEYER

[2] Mark McClure - comment

[3] sion and conformal dynamics II: Geometrically finite rational maps by Curtis T McMullen

[4] COMPLEX ANALYTIC DYNAMICS ON THE RIEMANN SPHERE BY PAUL BLANCHARD

[5] Inverse Iteration Algorithms for Julia Sets by Mark McClure

[6] wikipedia : Multibrot_set

[7] High-Order Mandelbrot and Julia Sets Written by Christopher Thomas. Images and Perl program

[8] Stephen Haas : The Hausdorff Dimension of the Julia Set of Polynomials of the Form z^d+c

[9] video on youtube by rrwick

[10] Desenvolupament_de_fractals_mitjan

[11] De la génération des fractales Théorie et Applications John Bonobo

[12] wolfram : julia-set-explorations

[13] C. McMullen, Automorphisms of rational maps. In `Holomorphic Functions and Moduli I', 31-60, Springer-Verlag, 1988.

[14] Hyperbolic components of McMullen maps Weiyuan Qiu, Pascale Roesch, Xiaoguang Wang, Yongcheng Yin

[15] "Visualizing the complex dynamics of families of polynomials with symmetric critical points" by Ning Chena, Jing Suna, Yan-ling Suna, Ming Tangb. Chaos, Solitons & Fractals. Volume 42, Issue 3, 15 November 2009, Pages 1611–1622

[16] A topological characterisation of holomorphic parabolic germs in the plane Fr ́ed ́eric Le Roux

[17] One approach to the digital visualization of hedgehogs in holomorphic dynamics Alessandro Rosa, fig 5.13 page 26

[18] A parabolic Pommerenke-Levin-Yoccoz inequality by Xavier Buff and Adam L. Epstein, fig 1 page 4

[19] Mandel: software for real and complex dynamics by Wolf Jung

[20] Complex dynamics, Lennart Carleson, Theodore W. Gamelin, Springer, 1993, ISBN 978-0-387-97942-7. Page 40, Figure 2.

[21] F. Bracci, Local holomorphic dynamics of diffeomorphisms in dimension one. Contemporary Mathematics 525, (2010), 1-42. Notes of the PhD course given in A.A 2007/08.

[22] Complex dynamics, Lennart Carleson, Theodore W. Gamelin, Springer, 1993, ISBN 978-0-387-97942-7. Page 41

[23] Mark McClure in stackexchange questions : what-is-the-shape-of-parabolic-critical-orbit

[24] One approach to the digital visualization of hedgehogs in holomorphic dynamics Alessandro Rosa

[25] stackexchange questions : what-is-the-shape-of-parabolic-critical-orbit

[26] Fractals by Anne Burns, Department of Mathematics, C.W. Post Campus, Long Island University

[27] Some Julia sets 2 by Michael Becker

[28] Fixpunkte und Periodische Punkte by Michael Becker

z(1 + z)^d

mz(1+z^(k*n))

z(1-z^q)

z^n+ z + c

z^n + c^p

z^n + c

z^2+c

z^3 + c

z^5 + c

z^10 + c

zn + 1/c

z^n + m*z^(-d)

z^n + m*z

z^2+m*z

z^3+m*z

dynamic planes

z^3 + z

z^4 + mz

Parameter plane

Period 1 components

Dynamic planes

z^4+z

z^4-iz

z^4 -z

z^5 + m*z

dynamic planes

z^5 + z

z^6+m*z

dynamical plane

z^14 + m*z

dynamic plane

z^14 - z

z^15 +m*z

dynamic plane

z^15-z

Other

z^5+m*z^4+z

Inside dynamics under generalized power setting

See also

References

zⁿ + 1/c