< Fractals < Iterations in the complex plane
Topologist's single comb
The intricated double comb for r=3/4
Heggehog example
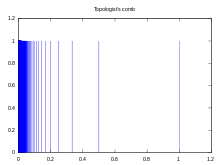
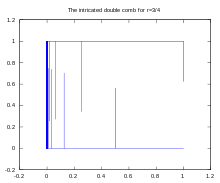
            The problem is that we are exploring environments based upon irrational numbers through computer machinery which works with finite rationals ! ( Alessandro Rosa )
  • there are Cremer Julia set for quadratic polynomial,
  • there are no images of such Julia sets
  • A Cremer Julia set has no interior and can never disconnect the plane [1]
  • It contains single or double comb.[2] "Objects such as combs (homeomorphs of the product of a Cantor set and an interval) had been expected to be found within hedgehogs." (Kingshook Biswas [3]
  • Cremer Julia sets are not locally connected [4][5]
  • "Hedgehogs associated to an indifferent irrational non-linearizable fixed point are full non-trivial compact connected sets totally invariant by the dynamics." R. PEREZ-MARCO[6]
  • a Cremer fixed point belongs to the Julia set[7]

Parameter

For Cremer Julia set internal angle should be non-Brjuno number (irrational number, non-diophantine ).

"The Cremer parameters are on the boundaries of hyperbolic components at specific internal angles (argument of the mulitplier). If you know the angle, you can compute the parameter explicitly for periods 1, 2, 3 and numerically for all periods. If I remember correctly, a simple angle is .01001000100001000001 ... times 2PI. But of course there are Siegel angles and parabolic angles which are the same for the first 100 digits. numerically there is no difference between Cremer, locally connected Siegel, non-locally connected Siegel, and parabolic with a high rotation number. ... Maybe that is one of the reasons, why you cannot draw them..." Wolf Jung

"A Cremer internal angle is obtained as 0.10001000000000000010000... with fast growing 0-gaps, but any finite approximation is parabolic." ( Wolf Jung )

Model

One can think about Cremer Julia set as :

  • parabolic Julia set with infinite period
  • Julia set with Siegel disk with infinite many digits

Models

  • Rempe’s straight brush model
  • Pseudo hedgehogs by Cheritat[8]

Hegdehogs

description[9]

  • non-linearizable [10]
  • Hedgehog space [11]

small cycles

"the “small cycles property”: Every neighborhood of the origin contains infinitely many periodic orbits " ( CREMER FIXED POINTS AND SMALL CYCLES by LIA PETRACOVICI )[12]

External rays

Parameter ray

" For Cremer parameters, there is a unique parameter ray landing, but the dynamics is more complicated." ( Wolf Jung )

Non-computable Julia sets

References

  1. ↑ mathoverflow.net questions : contractibility-of-connected-holomorphic-dynamics/149170#149170
  2. ↑ Describing quadratic Cremer point polynomials by parabolic perturbations by DAN ERIK KRARUP SØRENSEN. Ergodic Theory and Dynamical Systems (1998), 18 : pp 739-758. 1998 Cambridge University
  3. ↑ Hedgehogs of Hausdorff dimension one by Kingshook Biswas
  4. ↑ wikipedia : Locally connected space
  5. ↑ Smooth Combs Inside Hedgehogs by Kingshook Biswas
  6. ↑ ON QUASI-INVARIANT CURVES by Ricardo Pérez-Marco
  7. ↑ NON-ACCESSIBLE CRITICAL POINTS OF CERTAIN RATIONAL FUNCTIONS WITH CREMER POINTS by Lia Petracovici
  8. ↑ Cheritat galery of images
  9. ↑ Dynamical charts for irrationally indifferent fixed points of holomorphic functions by Mitsuhiro Shishikura
  10. ↑ Hedgehogs hunting with Cantor, Hausdorff and Liouville Alessandro Rosa
  11. ↑ wikipedia :Hedgehog space
  12. ↑ CREMER FIXED POINTS AND SMALL CYCLES by LIA PETRACOVICI
  13. ↑ CONSTRUCTING NON-COMPUTABLE JULIA SETS by M. BRAVERMAN AND M. YAMPOLSKY
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.