Priemgetalstelling

Werkelijk aantal priemgetallen (paars) en ${\displaystyle x/\ln(x)}$ (groen)

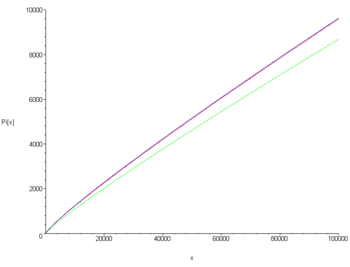
Laat ${\displaystyle \pi (x)}$ de priemgetal-telfunctie zijn die voor ieder reëel getal ${\displaystyle x}$ het aantal priemgetallen kleiner dan of gelijk aan x geeft. Een voorbeeld is ${\displaystyle \pi (10)=4;}$ dit omdat er precies vier priemgetallen, nl. 2, 3, 5 en 7, kleiner dan of gelijk aan 10 zijn. De priemgetalstelling stelt dan dat de limiet van het quotiënt van de twee functies ${\displaystyle \pi (x)}$ en ${\displaystyle x/\ln(x)}$ gelijk is aan 1 als ${\displaystyle x}$ tot oneindig nadert. In formule:

${\displaystyle \lim _{x\to \infty }{\frac {\pi (x)}{x/\ln(x)}}=1.}$

Deze formule staat bekend als de asymptotische verdelingswet van de priemgetallen. Dit wordt ook wel uitgedrukt als

${\displaystyle \pi (x)\sim {\frac {x}{\ln x}}.}$

Deze notatie en ook de stelling zeggen niets over de limiet van het verschil van de twee functies als ${\displaystyle x}$ tot oneindig nadert. Het verschil gedraagt zich zeer gecompliceerd, en het verschil is nauw gerelateerd aan de Riemann-hypothese. De priemgetalstelling zegt dat ${\displaystyle x/\ln(x)}$ nadert tot ${\displaystyle \pi (x)}$ in de zin dat de relatieve fout van deze benadering tot 0 nadert, als ${\displaystyle x}$ tot oneindig nadert.

De priemgetalstelling is equivalent aan de stelling dat het ${\displaystyle n}$-de priemgetal ${\displaystyle p_{n}}$ ongeveer gelijk is aan ${\displaystyle n\,\ln(n),}$ waar de relatieve fout van deze benadering opnieuw tot 0 nadert als ${\displaystyle n}$ tot oneindig nadert.

Gebaseerd op de priemgetallentabellen van Anton Felkel en Jurij Vega uitte Adrien-Marie Legendre in 1796 het vermoeden dat ${\displaystyle \pi (x)}$ wordt benaderd door de functie ${\displaystyle x/\ln(x)-B,}$ waarin ${\displaystyle B=1{.}08\ldots }$ een constante dicht bij 1 is. Carl Friedrich Gauss beschouwde ongeveer tegelijkertijd met Legendre hetzelfde vraagstuk. Op basis van de voorliggende berekeningen en enige heuristische redeneringen kwam hij met zijn eigen benaderingsfunctie, de logaritmische integraal ${\displaystyle \mathrm {li} (x).}$ Gauss publiceerde zijn resultaten echter niet. De formules van zowel Legendre als Gauss impliceren, zoals hierboven is uitgelegd, dezelfde asymptotische gelijkwaardigheid van ${\displaystyle \pi (x)}$ en ${\displaystyle x/\ln(x).}$ Wel blijkt de benadering van Gauss aanzienlijk beter te zijn, als men verschillen in plaats van quotiënten beschouwt.

In twee artikelen uit 1848 en 1850 heeft de Russische wiskundige Pafnoeti Tsjebysjev geprobeerd de asymptotische verdelingwet van de priemgetallen te bewijzen. Zijn werk valt op door het gebruik van de zèta-functie ${\displaystyle \zeta (s),}$ nog voor de beroemde verhandeling van Riemann uit 1859. Tsjebysjev slaagde erin een iets zwakkere vorm van de asymptotische verdelingswet te bewijzen, namelijk dat, als de limiet van ${\displaystyle \pi (x)/(x/\ln(x)),}$ voor ${\displaystyle x}$ naar oneindig, bestaat, deze limiet noodzakelijkerwijs gelijk is aan 1. Hij was in staat om zonder voorbehoud te bewijzen dat dit quotiënt voor elke ${\displaystyle x}$ begrensd wordt door twee expliciet gegeven constanten. Hoewel Tsjebysjev in zijn artikel de priemgetalstelling niet helemaal bewees, gebruikte hij zijn schattingen voor ${\displaystyle \pi (x)}$ om het postulaat van Bertrand, dat er voor ${\displaystyle n\geq 2}$ een priemgetal tussen ${\displaystyle n}$ en ${\displaystyle 2n}$ bestaat, te bewijzen.

Zonder twijfel het belangrijkste werk over de verdeling van de priemgetallen was de verhandeling van Riemann uit 1859, Over het aantal priemgetallen kleiner dan een gegeven hoeveelheid, het enige artikel dat Riemann ooit over dit onderwerp heeft geschreven. Riemann voerde revolutionaire ideeën over dit onderwerp in. Het belangrijkste daarvan is het idee dat de verdeling van priemgetallen nauw verbonden is aan de nulpunten van de analytisch verlengde Riemann-zèta-functie van een complexe variabele. In het bijzonder in deze verhandeling brengt Riemann zijn idee tot uitvoer om methoden uit de complexe analyse bij het bestuderen van de reële functie ${\displaystyle \pi (x)}$ te gebruiken. Voortbordurend op deze diepe ideeën van Riemann slaagden Hadamard en de la Vallée Poussin er onafhankelijk van elkaar in, om bijna veertig jaar na Riemann, in hetzelfde jaar (1896) de asymptotische verdelingswet van de priemgetallen te bewijzen. Beide bewijzen maakten van methoden uit de complexe analyse gebruik, waarbij zij als een belangrijke stap in het bewijs vaststelden dat de Riemann-zèta-functie ${\displaystyle \zeta (s)}$ ongelijk aan nul is voor alle complexe waarden van de variabele ${\displaystyle s}$ die van de vorm ${\displaystyle s=1+it}$ met ${\displaystyle t>0}$ zijn.[1]

Tijdens de 20e eeuw kwamen de stellingen van Hadamard en de la Vallée Poussin ook bekend te staan als de priemgetalstelling. Er werden verschillende nieuwe bewijzen van de priemgetalstelling gevonden, daaronder ook de "elementaire" bewijzen van Atle Selberg en Paul Erdős (1949).

• (en) John Derbyshire, Prime Obsession, Bernhard Riemann and the Greatest Unsolved Problem in Mathematics, London, 2003, ISBN 0-452-28525-9
• (en) Marcus du Sautoy, The Music of the Primes, why an unsolved problem in mathematics matters, London, 2003, ISBN 1-84115-580-2
• (nl) Roland van der Veen, Jan van de Craats, De Riemann-hypothese: een miljoenenprobleem, Epsilon, 2011, ISBN 978-90-5041-126-4