Lax–Friedrichs method

Consider a one-dimensional, linear hyperbolic partial differential equation for ${\displaystyle u(x,t)}$ of the form:

${\displaystyle u_{t}+au_{x}=0\,}$

on the domain

${\displaystyle b\leq x\leq c,\;0\leq t\leq d}$

with initial condition

${\displaystyle u(x,0)=u_{0}(x)\,}$

and the boundary conditions

${\displaystyle u(b,t)=u_{b}(t)\,}$

${\displaystyle u(c,t)=u_{c}(t).\,}$

If one discretizes the domain ${\displaystyle (b,c)\times (0,d)}$ to a grid with equally spaced points with a spacing of ${\displaystyle \Delta x}$ in the ${\displaystyle x}$-direction and ${\displaystyle \Delta t}$ in the ${\displaystyle t}$-direction, we define

${\displaystyle u_{i}^{n}=u(x_{i},t^{n}){\text{ with }}x_{i}=b+i\,\Delta x,\,t^{n}=n\,\Delta t{\text{ for }}i=0,\ldots ,N,\,n=0,\ldots ,M,}$

where

${\displaystyle N={\frac {c-b}{\Delta x}},\,M={\frac {d}{\Delta t}}}$

are integers representing the number of grid intervals. Then the Lax–Friedrichs method for solving the above partial differential equation is given by:

${\displaystyle {\frac {u_{i}^{n+1}-{\frac {1}{2}}(u_{i+1}^{n}+u_{i-1}^{n})}{\Delta t}}+a{\frac {u_{i+1}^{n}-u_{i-1}^{n}}{2\,\Delta x}}=0}$

Or, rewriting this to solve for the unknown ${\displaystyle u_{i}^{n+1},}$

${\displaystyle u_{i}^{n+1}={\frac {1}{2}}(u_{i+1}^{n}+u_{i-1}^{n})-a{\frac {\Delta t}{2\,\Delta x}}(u_{i+1}^{n}-u_{i-1}^{n})\,}$

Where the initial values and boundary nodes are taken from

${\displaystyle u_{i}^{0}=u_{0}(x_{i})}$

${\displaystyle u_{0}^{n}=u_{b}(t^{n})}$

${\displaystyle u_{N}^{n}=u_{c}(t^{n}).}$

A nonlinear hyperbolic conservation law is defined through a flux function ${\displaystyle f}$:

${\displaystyle u_{t}+(f(u))_{x}=0.}$

In the case of ${\displaystyle f(u)=au}$, we end up with a scalar linear problem. Note that in general, ${\displaystyle u}$ is a vector with ${\displaystyle m}$ equations in it. The generalization of the Lax-Friedrichs method to nonlinear systems takes the form[1]

${\displaystyle u_{i}^{n+1}={\frac {1}{2}}(u_{i+1}^{n}+u_{i-1}^{n})-{\frac {\Delta t}{2\,\Delta x}}(f(u_{i+1}^{n})-f(u_{i-1}^{n})).}$

This method is conservative and first order accurate, hence quite dissipative. It can, however be used as a building block for building high-order numerical schemes for solving hyperbolic partial differential equations, much like Euler time steps can be used as a building block for creating high-order numerical integrators for ordinary differential equations.

We note that this method can be written in conservation form:

${\displaystyle u_{i}^{n+1}=u_{i}^{n}-{\frac {\Delta t}{\Delta x}}\left({\hat {f}}_{i+1/2}^{n}-{\hat {f}}_{i-1/2}^{n}\right),}$

where

${\displaystyle {\hat {f}}_{i-1/2}^{n}={\frac {1}{2}}\left(f_{i-1}+f_{i}\right)-{\frac {\Delta x}{2\Delta t}}\left(u_{i}^{n}-u_{i-1}^{n}\right).}$

Without the extra terms ${\displaystyle u_{i}^{n}}$ and ${\displaystyle u_{i-1}^{n}}$ in the discrete flux, ${\displaystyle {\hat {f}}_{i-1/2}^{n}}$, one ends up with the FTCS scheme, which is well known to be unconditionally unstable for hyperbolic problems.

Example problem initial condition

Lax-Friedrichs solution

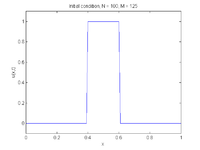
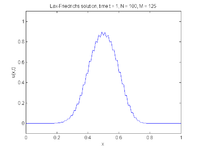
This method is explicit and first order accurate in time and first order accurate in space (${\displaystyle O(\Delta t)+O({\frac {\Delta x^{2}}{\Delta t}}))}$ provided ${\displaystyle u_{0}(x),\,u_{b}(t),\,u_{c}(t)}$ are sufficiently-smooth functions. Under these conditions, the method is stable if and only if the following condition is satisfied:

${\displaystyle \left|a{\frac {\Delta t}{\Delta x}}\right|\leq 1.}$

(A von Neumann stability analysis can show the necessity of this stability condition.) The Lax–Friedrichs method is classified as having second-order dissipation and third order dispersion (Chu 1978, pg. 304). For functions that have discontinuities, the scheme displays strong dissipation and dispersion (Thomas 1995, §7.8); see figures at right.

• DuChateau, Paul; Zachmann, David (2002), Applied Partial Differential Equations, New York: Dover Publications, ISBN 978-0-486-41976-3.
• Thomas, J. W. (1995), Numerical Partial Differential Equations: Finite Difference Methods, Texts in Applied Mathematics, 22, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97999-1.
• Chu, C. K. (1978), Numerical Methods in Fluid Mechanics, Advances in Applied Mechanics, 18, New York: Academic Press, ISBN 978-0-12-002018-8.
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 10.1.2. Lax Method", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8