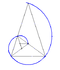
Hyperbolic spiral

Because of

${\displaystyle \lim _{\varphi \to 0}x=a\lim _{\varphi \to 0}{\frac {\cos \varphi }{\varphi }}=\infty ,\qquad \lim _{\varphi \to 0}y=a\lim _{\varphi \to 0}{\frac {\sin \varphi }{\varphi }}=a\cdot 1=a}$

the curve has an

• asymptote with equation ${\displaystyle \ y=a\;.}$

Definition of sector (light blue) and polar slope angle ${\displaystyle \alpha }$

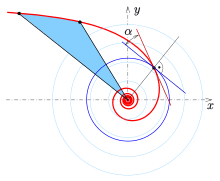
From vector calculus in polar coordinates one gets the formula ${\displaystyle \;\tan \alpha ={\tfrac {r'}{r}}\;}$ for the polar slope and its angle ${\displaystyle \alpha }$ between the tangent of a curve and the tangent of the corresponding polar circle.

For the hyperbolic spiral ${\displaystyle \;r={\tfrac {a}{\varphi }}\;}$ the polar slope is

• ${\displaystyle \tan \alpha ={\frac {-1}{\varphi }}.}$

The curvature of a curve with polar equation ${\displaystyle \;r=r(\varphi )\;}$ is ${\displaystyle \;\kappa ={\tfrac {r^{2}+2(r')^{2}-r\;r''}{(r^{2}+(r')^{2})^{3/2}}}\;.}$

From the equation ${\displaystyle r={\tfrac {a}{\varphi }}}$ and the derivatives ${\displaystyle \;r'={\tfrac {-a}{\varphi ^{2}}}\;}$ and ${\displaystyle \;r''={\tfrac {2a}{\varphi ^{3}}}\;}$ one gets the curvature of a hyperbolic spiral:

• ${\displaystyle \kappa (\varphi )={\frac {\varphi ^{4}}{a(\varphi ^{2}+1)^{3/2}}}.}$

The length of the arc of a hyperbolic spiral between ${\displaystyle \;(r(\varphi _{1}),\varphi _{1}),(r(\varphi _{2}),\varphi _{2})\;}$ can be calculated by the integral:

${\displaystyle L=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {\left(r^{\prime }(\varphi )\right)^{2}+r^{2}(\varphi )}}\,\mathrm {d} \varphi =\cdots =a\int \limits _{\varphi _{1}}^{\varphi _{2}}{\frac {\sqrt {1+\varphi ^{2}}}{\varphi ^{2}}}\,\mathrm {d} \varphi }$

${\displaystyle \qquad =a{\Big [}-{\frac {\sqrt {1+\varphi ^{2}}}{\varphi }}+\ln(\varphi +{\sqrt {1+\varphi ^{2}}}){\Big ]}_{\varphi _{1}}^{\varphi _{2}}\ .}$

The area of a sector (see diagram above) of a hyperbolic spiral with equation ${\displaystyle r={\tfrac {a}{\varphi }}}$ is:

${\displaystyle A={\tfrac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\;d\varphi ={\tfrac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\frac {a^{2}}{\varphi ^{2}}}\;d\varphi ={\frac {a}{2}}{\big (}{\frac {a}{\varphi _{1}}}-{\frac {a}{\varphi _{2}}}{\big )}}$

${\displaystyle \quad ={\frac {a}{2}}{\big (}r(\varphi _{1})-r(\varphi _{2}){\big )}\ .}$

Hyperbolic spiral (blue) as image of an Archimedean spiral (green) with an circle inversion

The inversion at the unit circle has in polar coordinates the simple description: ${\displaystyle \ (r,\varphi )\mapsto ({\tfrac {1}{r}},\varphi )\ }$.

• The image of an Archimedean spiral ${\displaystyle \;r={\tfrac {\varphi }{a}}\;}$ with a circle inversion is the hyperbolic spiral with equation ${\displaystyle \;r={\tfrac {a}{\varphi }}\;.}$

For ${\displaystyle \varphi =a}$ the two curves intersect at a fixpoint on the unit circle.

The osculating circle of the Archimedean spiral ${\displaystyle \;r={\tfrac {\varphi }{a}}\;}$ at the origin has radius ${\displaystyle \rho _{0}={\tfrac {1}{2a}}}$ (see Archimedean spiral) and the center ${\displaystyle (0,\rho _{0})}$. The image of this circle is the line ${\displaystyle y=a}$ (see circle inversion). Hence:

• The preimage of the asymptote of the hyperbolic spiral with the inversion of the Archimedean spiral is the osculating circle of the Archimedean spiral at the origin.

Example

The diagram shows an example with ${\displaystyle a=\pi }$.

Hyperbolic spiral as central projection of a helix

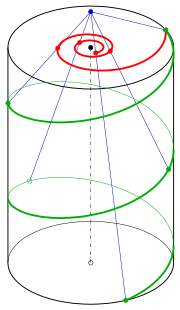
Consider the central projection from point ${\displaystyle C_{0}=(0,0,d)}$ onto the image plane ${\displaystyle z=0}$. This will map a point ${\displaystyle (x,y,z)}$ to the point ${\displaystyle \;{\tfrac {d}{d-z}}(x,y)\;.}$

The image under this projection of the helix with parametric representation

${\displaystyle (r\cos t,r\sin t,ct),\ c\neq 0\ ,}$

is the curve ${\displaystyle \;{\tfrac {dr}{d-ct}}(\cos t,\sin t)\;}$ with the polar equation

${\displaystyle \rho ={\frac {dr}{d-ct}}\;,}$

which describes a hyperbolic spiral.

For parameter ${\displaystyle \;t_{0}=d/c\;}$ the hyperbolic spiral has a pole and the helix intersects the plane ${\displaystyle \;z=d\;}$ at a point ${\displaystyle V_{0}}$. One can check by calculation that the image of the helix as it approaches ${\displaystyle V_{0}}$ is the asymptote of the hyperbolic spiral.