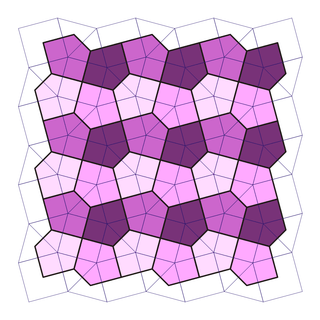
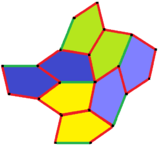
Cairo pentagonal tiling
In geometry, the Cairo pentagonal tiling is a dual semiregular tiling of the Euclidean plane. It is given its name because several streets in Cairo are paved in this design.[1][2] It is one of 15 known monohedral pentagon tilings. It is also called MacMahon's net[3] after Percy Alexander MacMahon and his 1921 publication New Mathematical Pastimes.[4] Conway calls it a 4-fold pentille.[5]
| Cairo pentagonal tiling | |
|---|---|
 | |
| Type | Dual semiregular tiling |
| Faces | irregular pentagons |
| Coxeter diagram | |
| Symmetry group | p4g, [4+,4], (4*2) p4, [4,4]+, (442) |
| Rotation group | p4, [4,4]+, (442) |
| Dual polyhedron | Snub square tiling |
| Face configuration | V3.3.4.3.4 |
| Properties | face-transitive |
As a 2-dimensional crystal net, it shares a special feature with the honeycomb net. Both nets are examples of standard realization, the notion introduced by M. Kotani and T. Sunada for general crystal nets.[6][7]
Geometry

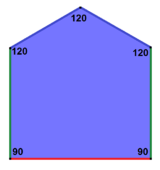
These are not regular pentagons: their sides are not equal (they have four long ones and one short one in the ratio 1:sqrt(3)-1[8]), and their angles in sequence are 120°, 120°, 90°, 120°, 90°. It is represented by with face configuration V3.3.4.3.4.
It is similar to the prismatic pentagonal tiling with face configuration V3.3.3.4.4, which has its right angles adjacent to each other.
Variations
The Cairo pentagonal tiling has two lower symmetry forms given as monohedral pentagonal tilings types 4 and 8:
| p4 (442) | pgg (22×) |
|---|---|
 |
 |
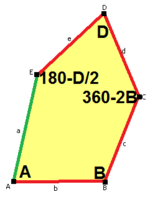
 b=c, d=e B=D=90° |
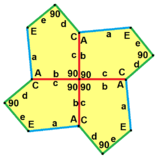
 b=c=d=e 2B+C=D+2E=360° |
 |
 |
Dual tiling
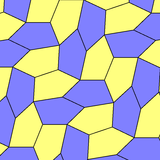
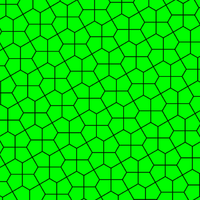
It is the dual of the snub square tiling, made of two squares and three equilateral triangles around each vertex.[9]
Relation to hexagonal tilings
This tiling can be seen as the union of two perpendicular hexagonal tilings, flattened by a ratio of . Each hexagon is divided into four pentagons. The two hexagons can also be distorted to be concave, leading to concave pentagons.[10] Alternately one of the hexagonal tilings can remain regular, and the second one stretched and flattened by in each direction, intersecting into 2 forms of pentagons.
 |
 |
 |
Topologically equivalent tilings
As a dual to the snub square tiling the geometric proportions are fixed for this tiling. However it can be adjusted to other geometric forms with the same topological connectivity and different symmetry. For example, this rectangular tiling is topologically identical.
 |
 |
 |
| Basketweave tiling | Cairo overlay | |
|---|---|---|
Truncated cairo pentagonal tiling
Truncating the 4-valence nodes creates a form related to the Goldberg polyhedra, and can be given the symbol {4+,4}2,1. The pentagons are truncated into heptagons. The dual {4,4+}2,1 has all triangle faces, related to the geodesic polyhedra. It can be seen as a snub square tiling with its squares replaced by 4 triangles.
 Truncated cairo pentagonal tiling |
 Kis snub square tiling |
Related polyhedra and tilings
The Cairo pentagonal tiling is similar to the prismatic pentagonal tiling with face configuration V3.3.3.4.4, and two 2-uniform dual tilings and 2 3-uniform duals which mix the two types of pentagons. They are drawn here with colored edges, or k-isohedral pentagons.[11]
 V3.3.3.4.4 |
 V3.3.4.3.4 |
| Related pentagonal tilings | |||||||
|---|---|---|---|---|---|---|---|
| Cairo pentagonal tiling | 2-uniform duals | ||||||
| p4g (4*2) | p2, (2222) | pgg (22×) | cmm (2*22) | ||||
 |  |
 |  |
 |  | ||
| V3.3.4.3.4 | (V3.3.3.4.4; V3.3.4.3.4) | ||||||
| Prismatic pentagonal tiling | 3-uniform duals | ||||||
| cmm (2*22) | p2 (2222) | pgg (22×) | p2 (2222) | pgg (22×) | |||
 |  |
 |  |
 |  | ||
| V3.3.3.4.4 | (V3.3.3.4.4; V3.3.4.3.4) | ||||||
The Cairo pentagonal tiling is in a sequence of dual snub polyhedra and tilings with face configuration V3.3.4.3.n.
| 4n2 symmetry mutations of snub tilings: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry 4n2 |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Snub figures |
 |
 |
 |
 |
 |
 |
 |
 |
| Config. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Gyro figures |
 |
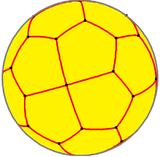 |
 |
 |
||||
| Config. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
It is in a sequence of dual snub polyhedra and tilings with face configuration V3.3.n.3.n.
| 4n2 symmetry mutations of snub tilings: 3.3.n.3.n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry 4n2 |
Spherical | Euclidean | Compact hyperbolic | Paracompact | |||||||
| 222 | 322 | 442 | 552 | 662 | 772 | 882 | ∞∞2 | ||||
| Snub figures |
 |
 |
 |
 |
 |
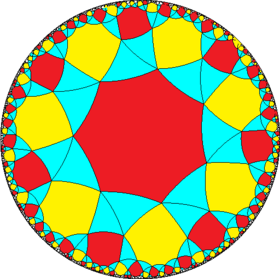 |
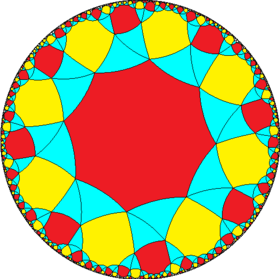 |
 | |||
| Config. | 3.3.2.3.2 | 3.3.3.3.3 | 3.3.4.3.4 | 3.3.5.3.5 | 3.3.6.3.6 | 3.3.7.3.7 | 3.3.8.3.8 | 3.3.∞.3.∞ | |||
| Gyro figures |
 |
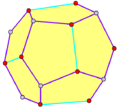 |
 |
 | |||||||
| Config. | V3.3.2.3.2 | V3.3.3.3.3 | V3.3.4.3.4 | V3.3.5.3.5 | V3.3.6.3.6 | V3.3.7.3.7 | V3.3.8.3.8 | V3.3.∞.3.∞ | |||
See also
| Wikimedia Commons has media related to Cairo pentagonal tiling. |
- Tilings of regular polygons
- List of uniform tilings
Notes
- Alsina, Claudi; Nelsen, Roger B. (2010), Charming proofs: a journey into elegant mathematics, Dolciani mathematical expositions, 42, Mathematical Association of America, p. 164, ISBN 978-0-88385-348-1.
- Martin, George Edward (1982), Transformation Geometry: An Introduction to Symmetry, Undergraduate Texts in Mathematics, Springer, p. 119, ISBN 978-0-387-90636-2.
- O'Keeffe, M.; Hyde, B. G. (1980), "Plane nets in crystal chemistry", Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 295 (1417): 553–618, doi:10.1098/rsta.1980.0150, JSTOR 36648.
- Macmahon, Major P. A. (1921), New Mathematical Pastimes, University Press. PDF p.101
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 Archived 2010-09-19 at the Wayback Machine (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p288 table)
- Kotani, M.; Sunada, T. (2000), "Standard realizations of crystal lattices via harmonic maps", Transactions of the American Mathematical Society, 353: 1–20, doi:10.1090/S0002-9947-00-02632-5
- T. Sunada, Topological Crystallography ---With a View Towards Discrete Geometric Analysis---, Surveys and Tutorials in the Applied Mathematical Sciences, Vol. 6, Springer
- http://catnaps.org/islamic/geometry2.html
- Weisstein, Eric W. "Dual tessellation". MathWorld.
- Defining a cairo type tiling
- Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.CS1 maint: ref=harv (link)
Further reading
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65) (Page 480, Tilings by polygons, #24 of 24 polygonal isohedral types by pentagons)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 38. ISBN 0-486-23729-X.
- Wells, David, The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 23, 1991.
- Keith Critchlow, Order in Space: A design source book, 1970, p. 77-76, pattern 3