Ratio test

In mathematics, the ratio test is a test (or "criterion") for the convergence of a series

\sum _{{n=1}}^{\infty }a_{n},

where each term is a real or complex number and $a n$ is nonzero when $n$ is large. The test was first published by Jean le Rond d'Alembert and is sometimes known as d'Alembert's ratio test or as the Cauchy ratio test.^[1]

The test

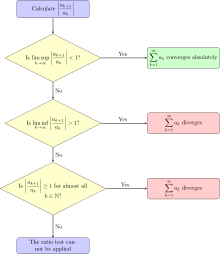
Decision diagram for the ratio test

The usual form of the test makes use of the limit

$L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\right|.$

(1)

The ratio test states that:

if L < 1 then the series converges absolutely;
if L > 1 then the series is divergent;
if L = 1 or the limit fails to exist, then the test is inconclusive, because there exist both convergent and divergent series that satisfy this case.

It is possible to make the ratio test applicable to certain cases where the limit L fails to exist, if limit superior and limit inferior are used. The test criteria can also be refined so that the test is sometimes conclusive even when L = 1. More specifically, let

R = \lim\sup \left|\frac{a_{n+1}}{a_n}\right|

r = \lim\inf \left|\frac{a_{n+1}}{a_n}\right|

.

Then the ratio test states that:^[2]^[3]

if R < 1, the series converges absolutely;
if r > 1, the series diverges;
if $\left|\frac{a_{n+1}}{a_n}\right|\ge 1$ for all large n (regardless of the value of r), the series also diverges; this is because $|a_n|$ is nonzero and increasing and hence $a n$ does not approach zero;
the test is otherwise inconclusive.

If the limit L in (1) exists, we must have L = R = r. So the original ratio test is a weaker version of the refined one.

Examples

Convergent because L < 1

Consider the series or sequence of series

\sum_{n=1}^\infty\frac{n}{e^n}

Applying the ratio test, one computes the limit

L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\right|=\lim _{{n\to \infty }}\left|{\frac {{\frac {n+1}{e^{{n+1}}}}}{{\frac {n}{e^{n}}}}}\right|={\frac {1}{e}}<1.

Since this limit is less than 1, the series converges.

Divergent because L > 1

Consider the series

\sum_{n=1}^\infty\frac{e^n}{n}.

Putting this into the ratio test:

L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\right|=\lim _{{n\to \infty }}\left|{\frac {{\frac {e^{{n+1}}}{n+1}}}{{\frac {e^{n}}{n}}}}\right|=e>1.

Thus the series diverges.

Inconclusive because L = 1

Consider the three series

\sum_{n=1}^\infty 1,

\sum _{{n=1}}^{\infty }{\frac {1}{n^{2}}},

\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}.

The first series (1 + 1 + 1 + 1 + ⋯) diverges, the second one (the one central to the Basel problem) converges absolutely and the third one (the alternating harmonic series) converges conditionally. However, the term-by-term magnitude ratios $\left|\frac{a_{n+1}}{a_n}\right|$ of the three series are respectively $1,$ $\frac{n^2}{(n+1)^2}$ and $\frac{n}{n+1}$ . So, in all three cases, one has that the limit $\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|$ is equal to 1. This illustrates that when L = 1, the series may converge or diverge, and hence the original ratio test is inconclusive. In such cases, more refined tests are required to determine convergence or divergence.

Proof

In this example, the ratio of adjacent terms in the blue sequence converges to L=1/2. We choose r = (L+1)/2 = 3/4. Then the blue sequence is dominated by the red sequence

r k

for all n ≥ 2. The red sequence converges, so the blue sequence does as well.

Below is a proof of the validity of the original ratio test.

Suppose that $L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{{n}}}}\right|<1$ . We can then show that the series converges absolutely by showing that its terms will eventually become less than those of a certain convergent geometric series. To do this, let $r = \frac{L+1}{2}$ . Then r is strictly between L and 1, and $|a_{n+1}| < r |a_{n}|$ for sufficiently large n (say, n greater than N). Hence $|a_{n+i}| < r^i|a_{n}|$ for each n > N and i > 0, and so

\sum _{{i=N+1}}^{{\infty }}|a_{i}|=\sum _{{i=1}}^{{\infty }}\left|a_{{N+i}}\right|<\sum _{{i=1}}^{{\infty }}r^{{i}}|a_{{N+1}}|=|a_{{N+1}}|\sum _{{i=1}}^{{\infty }}r^{{i}}=|a_{{N+1}}|{\frac {r}{1-r}}<\infty .

That is, the series converges absolutely.

On the other hand, if L > 1, then $|a_{n+1}| > |a_{n}|$ for sufficiently large n, so that the limit of the summands is non-zero. Hence the series diverges.

Extensions for L = 1

As seen in the previous example, the ratio test may be inconclusive when the limit of the ratio is 1. Extensions to ratio test, however, sometimes allows one to deal with this case. For instance, the aforementioned refined version of the test handles the case

\left|{\frac {a_{{n+1}}}{a_{n}}}\right|\geq 1.

Below are some other extensions. In all the tests below we assume that Σa_n is a sum with positive a_n.

Raabe's test

This extension is due to Joseph Ludwig Raabe. It states that if

\lim _{n\to \infty }n\left({\frac {a_{n}}{a_{n+1}}}-1\right)=R,

then the series will be convergent if R > 1 (this includes the case R = ∞) and divergent if R < 1.^[4] If R = 1, the test is inconclusive. d'Alembert's ratio test and Raabe's test are the first and second theorems in a hierarchy of such theorems due to Augustus De Morgan.

Proof of the validity of Raabe's test

Say $\delta _{n}=n\left({\frac {a_{n}}{a_{n+1}}}-1\right)$ . In fact we need not assume the limit exists; if $\limsup \delta _{n}<1$ then $\sum a_{n}$ diverges, while if $\liminf \delta _{n}>1$ the sum converges.

The proof proceeds essentially by comparison with $\sum 1/n^{R}$ . Suppose first that $\limsup \delta _{n}<1$ . Of course if $\limsup \delta _{n}<0$ then $a_{n+1}\geq a_{n}$ for large $n$ , so the sum diverges; assume then that $0\leq \limsup \delta _{n}<1$ . There exists $R<1$ such that $\delta _{n}\leq R$ for all $n\geq N$ , which is to say that $a_{n}/a_{n+1}\leq \left(1+{\frac {R}{n}}\right)\leq e^{R/n}$ . Thus $a_{n+1}\geq a_{n}e^{-R/n}$ , which implies that $a_{n+1}\geq a_{N}e^{-R(1/N+\dots +1/n)}\geq ca_{N}e^{-R\log(n)}=ca_{N}/n^{R}$ for $n\geq N$ ; since $R<1$ this shows that $\sum a_{n}$ diverges.

The proof of the other half is entirely analogous, with most of the inequalities simply reversed. We need a preliminary inequality to use in place of the simple $1+t<e^{t}$ that was used above: Fix $R$ and $N$ . Note that $\log \left(1+{\frac {R}{n}}\right)={\frac {R}{n}}+O\left({\frac {1}{n^{2}}}\right)$ . So $\log \left(\left(1+{\frac {R}{N}}\right)\dots \left(1+{\frac {R}{n}}\right)\right)=R\left({\frac {1}{N}}+\dots +{\frac {1}{n}}\right)+O(1)=R\log(n)+O(1)$ ; hence $\left(1+{\frac {R}{N}}\right)\dots \left(1+{\frac {R}{n}}\right)\geq cn^{R}$ .

Suppose now that $\liminf \delta _{n}>1$ . Arguing as in the first paragraph, using the inequality established in the previous paragraph, we see that there exists $R>1$ such that $a_{n+1}\leq ca_{N}n^{-R}$ for $n\geq N$ ; since $R>1$ this shows that $\sum a_{n}$ converges.

Higher order tests

The next cases in de Morgan's hierarchy are Bertrand's and Gauss's test. Each test involves slightly different higher order asymptotics. Bertrand's test asserts that if

{\frac {a_{n}}{a_{n+1}}}=1+{\frac {1}{n}}+{\frac {\rho _{n}}{n\ln n}}

then the series converges if lim inf ρ_n > 1, and diverges if lim sup ρ_n < 1.^[5]

Gauss's test asserts that if

{\frac {a_{n}}{a_{n+1}}}=1+{\frac {h}{n}}+{\frac {C_{n}}{n^{r}}}

where r > 1 and C_n is bounded, then the series converges if h > 1 and diverges if h ≤ 1.^[6]

These are both special cases of Kummer's test. Let ζ_n be an auxiliary sequence of positive constants. Let

\rho = \lim_{n\to\infty} \left(\zeta_n \frac{a_n}{a_{n+1}} - \zeta_{n+1}\right).

Then if ρ > 0, the series converges. If ρ < 0 and Σ1/ζ_n diverges, then the series diverges. Otherwise the test is inconclusive.^[7]

Proof of Kummer's test

If $\rho >0$ then fix a positive number $0<\delta<\rho$ . There exists a natural number $N$ such that for every $n>N,$

\delta\leq\zeta_{n}\frac{a_{n}}{a_{n+1}}-\zeta_{n+1}.

Since $a_{n+1}>0$ , for every $n> N,$

0\leq \delta a_{n+1}\leq \zeta_{n}a_{n}-\zeta_{n+1}a_{n+1}.

In particular $\zeta_{n+1}a_{n+1}\leq \zeta_{n}a_{n}$ for all $n\geq N$ which means that starting from the index $N$ the sequence $\zeta_{n}a_{n}>0$ is monotonically decreasing and positive which in particular implies that it is bounded below by 0. Therefore the limit

\lim_{n\to\infty}\zeta_{n}a_{n}=L

exists.

This implies that the positive telescoping series

\sum_{n=1}^{\infty}\left(\zeta_{n}a_{n}-\zeta_{n+1}a_{n+1}\right)

is convergent,

and since for all $n>N,$

\delta a_{n+1}\leq \zeta_{n}a_{n}-\zeta_{n+1}a_{n+1}

by the direct comparison test for positive series, the series $\sum_{n=1}^{\infty}\delta a_{n+1}$ is convergent.

On the other hand, if $\rho<0$ , then there is an N such that $\zeta_n a_n$ is increasing for $n>N$ . In particular, there exists an $\epsilon >0$ for which $\zeta_n a_n>\epsilon$ for all $n>N$ , and so $\sum_n a_n=\sum_n \frac{a_n\zeta_n}{\zeta_n}$ diverges by comparison with $\sum_n \frac \epsilon {\zeta_n}$ .

Footnotes

References

d'Alembert, J. (1768), Opuscules, V, pp. 171–183 .
Apostol, Tom M. (1974), Mathematical analysis (2nd ed.), Addison-Wesley, ISBN 978-0-201-00288-1 : §8.14.
Knopp, Konrad (1956), Infinite Sequences and Series, New York: Dover publications, Inc., ISBN 0-486-60153-6 : §3.3, 5.4.
Rudin, Walter (1976), Principles of Mathematical Analysis (3rd ed.), New York: McGraw-Hill, Inc., ISBN 0-07-054235-X : §3.34.
Hazewinkel, Michiel, ed. (2001) [1994], "Bertrand criterion", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
Hazewinkel, Michiel, ed. (2001) [1994], "Gauss criterion", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
Hazewinkel, Michiel, ed. (2001) [1994], "Kummer criterion", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
Watson, G. N.; Whittaker, E. T. (1963), A Course in Modern Analysis (4th ed.), Cambridge University Press, ISBN 0-521-58807-3 : §2.36, 2.37.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-1] Weisstein, Eric W. "Ratio Test". MathWorld.

[2] Rudin 1976, §3.34

[3] Apostol 1974, §8.14

[4] Weisstein, Eric W. "Raabe's Test". MathWorld.

[5] Weisstein, Eric W. "Bertrand's Test". MathWorld.

[6] Weisstein, Eric W. "Gauss's Test". MathWorld.

[7] Weisstein, Eric W. "Kummer's Test". MathWorld.