Maximal entropy random walk

Maximal entropy random walk (MERW) is a popular type of biased random walk on a graph, in which transition probabilities are chosen accordingly to the principle of maximum entropy, which says that the probability distribution which best represents the current state of knowledge is the one with largest entropy. While standard random walk chooses for every vertex uniform probability distribution among its outgoing edges, locally maximizing entropy rate, MERW maximizes it globally (average entropy production) by assuming uniform probability distribution among all paths in a given graph.

MERW is used in various fields of science. A direct application is choosing probabilities to maximize transmission rate through a constrained channel, analogously to Fibonacci coding. Its properties also made it useful for example in analysis of complex networks,^[1] like link prediction,^[2] community detection^[3] and centrality measures.^[4] Also in image analysis, for example for detecting visual saliency regions,^[5] object localization,^[6] tampering detection^[7] or tractography problem.^[8]

Additionally, it recreates some properties of quantum mechanics, suggesting a way to repair the discrepancy between diffusion models and quantum predictions, like Anderson localization.^[9]

Basic model

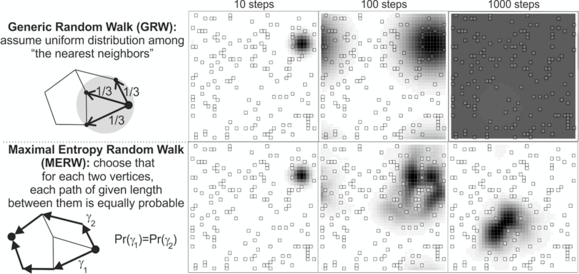
Left: basic concept of the generic random walk (GRW) and maximal entropy random walk (MERW)
Right: example of their evolution on the same inhomogeneous 2D lattice with cyclic boundary conditions – probability density after 10, 100 and 1000 steps while starting from the same vertex. The small boxes represent defects: all vertices but the marked ones have additional self-loop (edge to itself). For regular lattices (no defects), GRW and MERW are identical. While defects do not strongly affect the local behavior, they lead to a completely different global stationary probability here. While GRW (and based on it standard diffusion) leads to nearly uniform stationary density, MERW has strong localization property, imprisoning the walkers in entropic wells in analogy to electrons in defected lattice of semi-conductor.

Imagine there is a graph given by adjacency matrix: $A_{ij}=1$ if there is an edge from vertex $i$ to $j$ , 0 otherwise. For simplicity assume it is an undirected graph, what corresponds to symmetric $A$ , however, MERW can be also generalized for directed and weighted graphs (getting Boltzmann distribution among paths instead of uniform).

We would like to choose a random walk as Markov process on this graph: for every vertex $i$ and its outgoing edge to $j$ , choose probability $S_{ij}$ of the walker randomly using this edge after visiting $i$ . Formally, choose $S_{ij}$ stochastic matrix such that $0\leq S_{ij}\leq A_{ij},\ \sum _{j}S_{ij}=1$ . Assuming this graph is connected and not periodic, ergodic theory says that evolution of this stochastic process leads to some stationary probability distribution $\rho _{i}$ , such that $\sum _{i}\rho _{i}S_{ij}=\rho _{j}$ .

Using Shannon entropy for every vertex and averaging over probability of visiting this vertex (to be able to use its entropy), we get the following formula for average entropy production (entropy rate) of a stochastic process:

H(S)=\sum _{i}\rho _{i}\sum _{j}S_{ij}\log(1/S_{ij})

This definition turns out to be equivalent with asymptotic average entropy (per length) of the probability distribution in the space of paths for this stochastic process.

In the standard random walk, referred here as generic random walk (GRW), we naturally choose that each outgoing edge is equally probable: $S_{ij}=A_{ij}/\sum _{k}A_{ik}$ . For a symmetric $A$ it leads to $\rho _{i}\propto \sum _{j}A_{ij}$ stationary probability distribution. It locally maximizes entropy production (uncertainty) for every vertex, but usually leads to a suboptimal averaged global entropy rate $H(S)$ .

MERW chooses the stochastic matrix which maximizes $H(S)$ , or equivalently assumes uniform probability distribution among all paths in a given graph. Its formula is obtained by first calculating the dominant eigenvalue and corresponding eigenvector of the adjacency matrix: $\max _{|\lambda |}\ \psi A=\lambda \psi$ . Then stochastic matrix and stationary probability distribution are given by:

S_{ij}={\frac {A_{ij}}{\lambda }}{\frac {\psi _{j}}{\psi _{i}}}\qquad \qquad \rho _{i}\propto \psi _{i}^{2}

for which every length $l$ possible path from $i$ to $j$ has probability ${\frac {1}{\lambda ^{l}}}{\frac {\psi _{j}}{\psi _{i}}}$ . Its entropy rate is $\log(\lambda )$ .

In contrast to GRW, the MERW transition probabilities generally depend on situation of the entire graph (are nonlocal). Hence, they rather should not be imagined as directly applied by the walker – if she performs randomly looking decisions based on local situation, like a person, the GRW approach is rather more appropriate. MERW is based on the principle of maximum entropy, making it the safest assumption when we don't have any additional knowledge about the system. For example to model our knowledge about an object performing some complex dynamics – not necessarily random, like a particle.

Sketch of derivation

Assume for simplicity that the considered graph is indirected, connected and aperiodic, what allows to conclude from the Perron-Frobenius theorem that the dominant eigenvector is unique. Hence $A^{l}$ can be asymptotically $(l\to \infty )$ approximated by $\lambda ^{l}\psi \psi ^{T}$ (or $\lambda ^{l}|\psi \rangle \langle \psi |$ in bra-ket notation).

MERW is uniform distribution among paths. The number of length $2l$ paths with vertex $i$ in the center is $\sum _{jk}(A^{l})_{ji}(A^{l})_{ik}$ what asymptotically grows like $\lambda ^{2l}\psi _{i}^{2}$ , getting the $\rho _{i}\propto \psi _{i}^{2}$ behavior.

Analogously calculating probability distribution for two succeeding vertices $ij$ , we get ${\textrm {Pr}}(ij)\propto \psi _{i}A_{ij}\psi _{j}$ . Dividing by ${\textrm {Pr}}(i)=\rho _{i}$ and normalizing to $\sum _{j}S_{ij}=1$ , we get $S_{ij}={\frac {A_{ij}}{\lambda }}{\frac {\psi _{j}}{\psi _{i}}}$ .

Examples

Left: choosing the optimal probability after symbol 0 in Fibonacci coding. Right: one-dimensional defected lattice and its stationary density for length 1000 cycle (it has three defects). While in standard random walk the stationary density is proportional to degree of a vertex, leading to 3/2 difference here, in MERW density is nearly completely localized in the largest defect-free region, analogous to the ground state predicted by quantum mechanics.

Let us first look at probably the simplest nontrivial situation: Fibonacci coding, where we want to transmit a message as a sequence of 0/1, but not using two successive 1s – after 1 there has to be used 0. To maximize the amount of information transmitted in such sequence, we should assume uniform probability distribution in the space of all possible sequences fulfilling this constraint. To practically use such long sequences, after 1 we have to use 0, but there remains a freedom of choosing the probability of 0 after 0. Let us denote this probability by $q$ , then entropy coding would allow to encode a message using this chosen probability distribution. The stationary probability distribution of symbols for a given $q$ turns out to be $\rho =(1/(2-q),1-1/(2-q))$ . Hence, entropy production is $H(S)=\rho _{0}\left(q\log(1/q)+(1-q)\log(1/(1-q))\right)$ , which is maximized for $q=({\sqrt {5}}-1)/2\approx 0.618$ , known from golden ratio. In contrast, standard random walk would choose suboptimal $q=0.5$ . While choosing larger $q$ reduces the amount of information produced after 0, it also reduces frequency of 1, after which we cannot write any information.

A more complex example is defected one-dimensional cyclic lattice: let say 1000 nodes connected in a ring, for which all nodes but the defects have self-loop (edge to itself). In standard random walk (GRW) the stationary probability distribution would have defect probability being 2/3 of probability of the remaining vertices – there is nearly no localization, also analogously for standard diffusion, which is infinitesimal limit of GRW. For MERW we have to first find the dominant eigenvector of the adjacency matrix – maximizing $\lambda$ in:

$(\lambda \psi )_{x}=(A\psi )_{x}=\psi _{x-1}+(1-V_{x})\psi _{x}+\psi _{x+1}$

for all positions $x$ , where $V_{x}=1$ for defects, 0 otherwise. Substituting $3\psi _{x}$ and multiplying the equation by −1 we get:

$E\psi _{x}=-(\psi _{x-1}-2\psi _{x}+\psi _{x+1})+V_{x}\psi _{x}$

where $E=3-\lambda$ is minimized now, becoming the analog of energy. The formula inside the bracket is discrete Laplace operator, making this equation a discrete analogue of stationary Schrodinger equation. Like in quantum mechanics, MERW predicts that the probability distribution should lead exactly to the one of quantum ground state: $\rho _{x}\propto \psi _{x}^{2}$ with its strongly localized density (in contrast to standard diffusion). Performing infinitesimal limit, we can get standard continuous stationary Schrodinger equation ( $E\psi =-C\psi _{xx}+V\psi$ for $C=\hbar ^{2}/2m$ ) here.^[10]

References

↑ R. Sinatra, J. Gómez-Gardenes, R. Lambiotte, V. Nicosia, Maximal-entropy random walks in complex networks with limited information, Phys. Rev. E, 2011.
↑ R.H. Li, J.X. Yu, J. Liu, Link Prediction: the Power of Maximal Entropy Random Walk, CIKM '11, 2011.
↑ J. Ochab, Z. Burda, Maximal entropy random walk in community detection, Z. Eur. Phys. J., 2013.
↑ J.C. Delvenne, A.S. Libert, Centrality measures and thermodynamic formalism for complex networks, Phys. Rev. E, 2011.
↑ J.G. Yu, J. Zhao, J. Tian, Y. Tan, Maximal entropy random walk for region-based visual saliency, IEEE Transactions on Cybernetics, 2014.
↑ L. Wang, J. Zhao, X. Hu, J. Lu, Weakly supervised object localization via maximal entropy random walk, ICIP, 2014.
↑ P. Korus, J. Huang, Improved Tampering Localization in Digital Image Forensics Based on Maximal Entropy Random Walk, IEEE Signal Processing Letters, 2016.
↑ V.L. Galinsky, L.R. Frank, Simultaneous multi-scale diffusion estimation and tractography guided by entropy spectrum pathways, IEEE Transactions on Medical Imaging, 2015.
↑ Z. Burda, J. Duda, J. M. Luck, and B. Waclaw, Localization of the Maximal Entropy Random Walk, Phys. Rev. Lett., 2009.
↑ J. Duda, Extended Maximal Entropy Random Walk, PhD Thesis, 2012.

External links

Gábor Simonyi, Y. Lin, Z. Zhang, "Mean first-passage time for maximal-entropy random walks in complex networks". Scientific Reports, 2014.
Electron Conductance Models Using Maximal Entropy Random Walks Wolfram Demonstration Project

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Sinatra-1] R. Sinatra, J. Gómez-Gardenes, R. Lambiotte, V. Nicosia, Maximal-entropy random walks in complex networks with limited information, Phys. Rev. E, 2011.

[link-2] R.H. Li, J.X. Yu, J. Liu, Link Prediction: the Power of Maximal Entropy Random Walk, CIKM '11, 2011.

[community-3] J. Ochab, Z. Burda, Maximal entropy random walk in community detection, Z. Eur. Phys. J., 2013.

[central-4] J.C. Delvenne, A.S. Libert, Centrality measures and thermodynamic formalism for complex networks, Phys. Rev. E, 2011.

[saliency-5] J.G. Yu, J. Zhao, J. Tian, Y. Tan, Maximal entropy random walk for region-based visual saliency, IEEE Transactions on Cybernetics, 2014.

[local-6] L. Wang, J. Zhao, X. Hu, J. Lu, Weakly supervised object localization via maximal entropy random walk, ICIP, 2014.

[tamp-7] P. Korus, J. Huang, Improved Tampering Localization in Digital Image Forensics Based on Maximal Entropy Random Walk, IEEE Signal Processing Letters, 2016.

[trac-8] V.L. Galinsky, L.R. Frank, Simultaneous multi-scale diffusion estimation and tractography guided by entropy spectrum pathways, IEEE Transactions on Medical Imaging, 2015.

[prl-9] Z. Burda, J. Duda, J. M. Luck, and B. Waclaw, Localization of the Maximal Entropy Random Walk, Phys. Rev. Lett., 2009.

[ext-10] J. Duda, Extended Maximal Entropy Random Walk, PhD Thesis, 2012.