Eckhaus equation

In mathematical physics, the Eckhaus equation – or the Kundu–Eckhaus equation – is a nonlinear partial differential equations within the nonlinear Schrödinger class:^[1]

i\psi _{t}+\psi _{{xx}}+2\left(|\psi |^{2}\right)_{x}\,\psi +|\psi |^{4}\,\psi =0.

The equation was independently introduced by Wiktor Eckhaus and by Anjan Kundu to model the propagation of waves in dispersive media.^[2]^[3] The Kundu–Eckhaus equation admits many different types of analytical solutions – just like the nonlinear Schrödinger equation – including but not limited to rational rogue wave solutions.^[4] Behavior of its stochastic rogue wave solutions and their spectra may be used for early detection purposes.^[5]

Linearization

Animation of a wave-packet solution of the Eckhaus equation. The blue line is the real part of the solution, the red line is the imaginary part and the black line is the wave envelope (absolute value). Note the asymmetry in the envelope

|\psi (x,t)|

for the Eckhaus equation, while the envelope

|\varphi (x,t)|

– of the corresponding solution to the linear Schrödinger equation – is symmetric (in

x

). The short waves in the packet propagate faster than the long waves.

Animation of the wave-packet solution of the linear Schrödinger equation – corresponding with the above animation for the Eckhaus equation. The blue line is the real part of the solution, the red line is the imaginary part, the black line is the wave envelope (absolute value) and the green line is the centroid of the wave packet envelope.

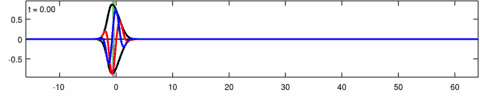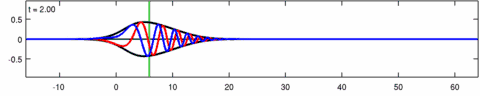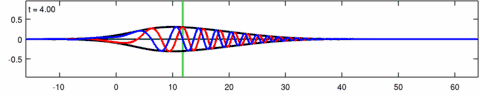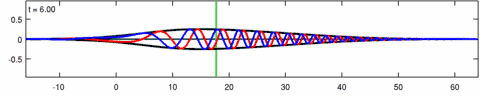
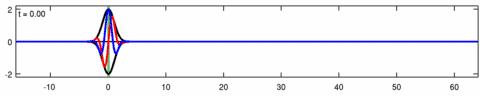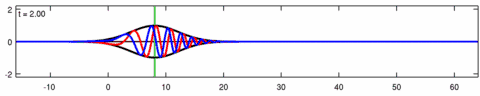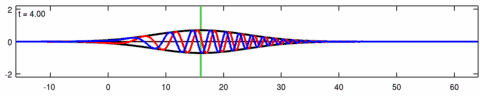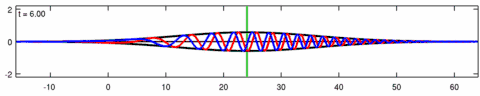
The Eckhaus equation can be linearized to the linear Schrödinger equation:^[6]

i\varphi _{t}+\varphi _{{xx}}=0,

through the non-linear transformation:^[7]

\varphi (x,t)=\psi (x,t)\,\exp \left(\int _{{-\infty }}^{x}|\psi (x^{\prime },t)|^{2}\;{\text{d}}x^{\prime }\right).

The inverse transformation is:

\psi (x,t)={\frac {\varphi (x,t)}{\displaystyle \left(1+2\,\int _{{-\infty }}^{x}|\varphi (x^{\prime },t)|^{2}\;{\text{d}}x^{\prime }\right)^{{1/2}}}}.

This linearization also implies that the Eckhaus equation is integrable.

Notes

References

Ablowitz, M.J.; Ahrens, C.D.; De Lillo, S. (2005), "On a "quasi" integrable discrete Eckhaus equation", Journal of Nonlinear Mathematical Physics, 12 (Supplement 1): 1–12, Bibcode:2005JNMP...12S...1A, doi:10.2991/jnmp.2005.12.s1.1
Calogero, F.; De Lillo, S. (1987), "The Eckhaus PDE iψ_t + ψ_xx+ 2(|ψ|²)_x ψ + |ψ|⁴ ψ = 0", Inverse Problems, 3 (4): 633–682, Bibcode:1987InvPr...3..633C, doi:10.1088/0266-5611/3/4/012
Eckhaus, W. (1985), The long-time behaviour for perturbed wave-equations and related problems, Department of Mathematics, University of Utrecht, Preprint no. 404 .
Published in part in: Eckhaus, W. (1986), "The long-time behaviour for perturbed wave-equations and related problems", in Kröner, E.; Kirchgässner, K., Trends in applications of pure mathematics to mechanics, Lecture Notes in Physics, 249, Berlin: Springer, pp. 168–194, doi:10.1007/BFb0016391, ISBN 978-3-540-16467-8
Bayindir, C. (2016a), "Rogue waves of the Kundu–Eckhaus equation in a chaotic wavefield", Physical Review E, 93 (032201), arXiv:1601.00209, Bibcode:2016PhRvE..93c2201B, doi:10.1103/PhysRevE.93.032201
Bayindir, C. (2016b), "Rogue wave spectra of the Kundu–Eckhaus equation", Physical Review E, 93 (062215), arXiv:1604.08035, Bibcode:2016PhRvE..93f2215B, doi:10.1103/PhysRevE.93.062215
Kundu, A. (1984), "Landau–Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations", Journal of Mathematical Physics, 25: 3433–3438, Bibcode:1984JMP....25.3433K, doi:10.1063/1.526113
Taghizadeh, N.; Mirzazadeh, M.; Tascan, F. (2012), "The first-integral method applied to the Eckhaus equation", Applied Mathematics Letters, 25 (5): 798–802, doi:10.1016/j.aml.2011.10.021
Zwillinger, D. (1998), Handbook of differential equations (3rd ed.), Academic Press, ISBN 978 0 12 784396 4

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Zwillinger (1998, pp. 177 & 390)

[2] Eckhaus (1985)

[3] Kundu (1984)

[4] Bayindir (2016a)

[5] Bayindir (2016b)

[6] Calogero & De Lillo (1987)

[7] Ablowitz, Ahrens & De Lillo (2005)