mandelbrot-numerics is a library for advanced numeric calculations related with Mandelbrot set by Claude Heiland-Allen.
This is unofficial wiki about it, containing most of maximus/book 'lib' and 'bin' (but no rendering)
See:
- dictionary
- notation
- fork of the library
Notation
directories
- bin for programs
- lib for functions with 2 versions
- d for double precision
- r for arbitrary precision
- include
precision
Precision here means precision of floating point numbers in the numerical computing.
It is a positive integer. It is a number of bits of binary number (
Function names ( notation)
- double precision: m_d_*()
- functions taking pointers to double _Complex use them for output
- arbitrary precision: m_r_*()
how to find precision ?
- start with minimal precision ( double = 53 bits )
- compute new precision = 53 + f(parameter) where parameter is a feature of the procedure ( for example minimal size of the component for m-interior ). In other words new precision is grater then 53
Installation
" you need to "make install" mandelbrot-symbolics lib before trying anything with mandelbrot-numerics"
dependencies
#include <complex.h>
#include <math.h>
#include <stdbool.h>
#include <stdint.h>
#include <stdlib.h>
#include <gmp.h>
#include <mpfr.h>
#include <mpc.h>
Gcc flags :
gcc -lmpc -lmpfr -lgmp -lm
From console :
sudo aptitude install libmpc-dev
git
clone
From directory in which you want to clone git repo:
git clone https://code.mathr.co.uk/mandelbrot-numerics.git
compile
and from the same directory :
make -C mandelbrot-numerics/c/lib prefix=${HOME}/opt install
make -C mandelbrot-numerics/c/bin prefix=${HOME}/opt install
then to run do:
export LD_LIBRARY_PATH=${HOME}/opt/lib
check :
echo $LD_LIBRARY_PATH
result :
/home/a/opt/lib
or
export PATH=${HOME}/opt/bin:${PATH}
and check :
echo $PATH
To set it permanently change file .profile[1]
test
m-describe 53 20 100 0 0 4
update
git
From console opened in the mandelbrot-numerics directory :
git pull
If you made some local changes you can undu them :
git checkout -f
then
git pull
Now install again
how to use it
- to include library c source should *only* have #include <mandelbrot-numerics.h>
- compile and link with pkg-config: see mandelbrot-numerics/c/bin/Makefile for an example
- quickest way to get started is to just put your file in mandelbrot-numerics/c/bin and run make
m-describe
This procedure gives description of point c from the parameter plane.
Use withote parameters:
m-describe
gives usage description:
usage: m-describe precision maxperiod maxiters re im ncpus
Check:
- point c = 0 = 0 +0*I= re+ im*I
- with precision = 53 bits
- max period= 20
- max iters = 100
m-describe 53 20 100 0 0 4
output is :
the input point was +0e+00 + +0e+00 i the point didn't escape after 100 iterations nearby hyperbolic components to the input point: - a period 1 cardioid with nucleus at +0e+00 + +0e+00 i the component has size 1.00000e+00 and is pointing west the atom domain has size 0.00000e+00 the atom domain coordinates of the input point are -nan + -nan i the atom domain coordinates in polar form are nan to the east the nucleus is 0.00000e+00 to the east of the input point the input point is interior to this component at radius 0.00000e+00 and angle 0.000000000000000000 (in turns) the multiplier is +0.00000e+00 + +0.00000e+00 i a point in the attractor is +0e+00 + +0e+00 i external angles of this component are: .(0) .(1)
shape
Versions
- m_d.shape.c
- m_r_shape.c
Description[2]
size
atom domain
Atom domain size estimate[3] [4]formula from
http://ibiblio.org/e-notes/MSet/windows.htm <-- where I got the formula from
component size
Files:
- m-size.c
- m_d_size.c
- output: complex double size
- m_r_size.c
- output : mpc_t size
Use without parameters:
./m-size
gives usage description :
usage: ./m-size precision nucleus-re nucleus-im period
Parameters:
Results are 2 numbers is:
- cabs(size), carg(size)
- mpc_abs(r, size, MPFR_RNDN); mpc_arg(t, size, MPFR_RNDN);
Example usage:
./m-size double 0 0 1
output :
1.0000000000000000e+00 0.0000000000000000e+00
In other words:
the component has size 1.00000e+00 and is pointing west
period
box-period
Computing period under complex quadratic polynomial
"But, the box period method detects the period of a *nucleus* within the box - if there is no nucleus there it will fail."
See:
binaries
m-box-period
The result :
usage: m-box-period precision center-re center-im radius maxperiod
code
This is one file program using code extracted from Claude's library.
/*
http://code.mathr.co.uk/mandelbrot-numerics/blob/HEAD:/c/bin/m-box-period.c
numerical algorithms related to the Mandelbrot set
by Claude Heiland-Allen
https://mathr.co.uk/blog/
GNU GENERAL PUBLIC LICENSE Version 3, 29 June 2007
http://code.mathr.co.uk/mandelbrot-numerics/blob/HEAD:/COPYING
mandelbrot-numerics
Numerical algorithms related to the Mandelbrot set: ray tracing, nucleus location, bond points, etc.
---------------------
Dependencies
sudo aptitude install libmpc-dev
---------------------------------
https://gitlab.com/adammajewski/mandelbrot-numerics-box-periood
Existing folder or Git repository
cd existing_folder
git init
git remote add origin git@gitlab.com:adammajewski/mandelbrot-numerics-box-periood.git
git add p.c
git commit -m "sasa"
git push -u origin master
-------------------
gcc p.c -lmpc -lmpfr -lgmp -Wall
./a.out precision center-re center-im radius maxperiod
./a.out 100 0.37496784 0.21687214 1.0 20
*/
#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>
#include <errno.h>
#include <string.h>
#include <math.h>
#include <complex.h>
#include <stdbool.h>
#include <gmp.h>
#include <mpfr.h>
#include <mpc.h>
// static const double twopi = 6.283185307179586;
/* --------------- http://code.mathr.co.uk/mandelbrot-numerics/blob_plain/HEAD:/c/lib/m_d_util.h ---- */
static inline int sgn(double z) {
if (z > 0) { return 1; }
if (z < 0) { return -1; }
return 0;
}
static inline bool odd(int a) {
return a & 1;
}
static inline double cabs2(double _Complex z) {
return creal(z) * creal(z) + cimag(z) * cimag(z);
}
static inline bool cisfinite(double _Complex z) {
return isfinite(creal(z)) && isfinite(cimag(z));
}
static const double pi = 3.141592653589793;
static const double twopi = 6.283185307179586;
// last . takeWhile (\x -> 2 /= 2 + x) . iterate (/2) $ 1 :: Double
static const double epsilon = 4.440892098500626e-16;
// epsilon^2
static const double epsilon2 = 1.9721522630525295e-31;
/* --------------- utils.h -------------------------------------- */
static inline bool arg_precision(const char *arg, bool *native, int *bits) {
if (0 == strcmp("double", arg)) {
*native = true;
*bits = 53;
return true;
} else {
char *check = 0;
errno = 0;
long int li = strtol(arg, &check, 10);
bool valid = ! errno && arg != check && ! *check;
int i = li;
if (valid && i > 1) {
*native = false;
*bits = i;
return true;
}
}
return false;
}
static inline bool arg_double(const char *arg, double *x) {
char *check = 0;
errno = 0;
double d = strtod(arg, &check);
if (! errno && arg != check && ! *check) {
*x = d;
return true;
}
return false;
}
static inline bool arg_int(const char *arg, int *x) {
char *check = 0;
errno = 0;
long int li = strtol(arg, &check, 10);
if (! errno && arg != check && ! *check) {
*x = li;
return true;
}
return false;
}
static inline bool arg_rational(const char *arg, mpq_t x) {
int ok = mpq_set_str(x, arg, 10);
mpq_canonicalize(x);
return ok == 0;
}
static inline bool arg_mpfr(const char *arg, mpfr_t x) {
return 0 == mpfr_set_str(x, arg, 10, MPFR_RNDN);
}
static inline bool arg_mpc(const char *re, const char *im, mpc_t x) {
int ok
= mpfr_set_str(mpc_realref(x), re, 10, MPFR_RNDN)
+ mpfr_set_str(mpc_imagref(x), im, 10, MPFR_RNDN);
return ok == 0;
}
/* -----------c/lib/m_d_box_period.c -----------------------*/
static double cross(double _Complex a, double _Complex b) {
return cimag(a) * creal(b) - creal(a) * cimag(b);
}
static bool crosses_positive_real_axis(double _Complex a, double _Complex b) {
if (sgn(cimag(a)) != sgn(cimag(b))) {
double _Complex d = b - a;
int s = sgn(cimag(d));
int t = sgn(cross(d, a));
return s == t;
}
return false;
}
static bool surrounds_origin(double _Complex a, double _Complex b, double _Complex c, double _Complex d) {
return odd
( crosses_positive_real_axis(a, b)
+ crosses_positive_real_axis(b, c)
+ crosses_positive_real_axis(c, d)
+ crosses_positive_real_axis(d, a)
);
}
typedef struct m_d_box_period {
double _Complex c[4];
double _Complex z[4];
int p;
} m_d_box_period_t ;
m_d_box_period_t *m_d_box_period_new(double _Complex center, double radius) {
m_d_box_period_t *box = (m_d_box_period_t *) malloc(sizeof(*box));
if (! box) {
return 0;
}
box->z[0] = box->c[0] = center + ((-radius) + I * (-radius));
box->z[1] = box->c[1] = center + (( radius) + I * (-radius));
box->z[2] = box->c[2] = center + (( radius) + I * ( radius));
box->z[3] = box->c[3] = center + ((-radius) + I * ( radius));
box->p = 1;
return box;
}
void m_d_box_period_delete(m_d_box_period_t *box) {
if (box) {
free(box);
}
}
extern bool m_d_box_period_step(m_d_box_period_t *box) {
if (! box) {
return false;
}
bool ok = true;
for (int i = 0; i < 4; ++i) {
box->z[i] = box->z[i] * box->z[i] + box->c[i];
ok = ok && cisfinite(box->z[i]);
}
box->p = box->p + 1;
return ok;
}
extern bool m_d_box_period_have_period(const m_d_box_period_t *box) {
if (! box) {
return true;
}
return surrounds_origin(box->z[0], box->z[1], box->z[2], box->z[3]);
}
extern int m_d_box_period_get_period(const m_d_box_period_t *box) {
if (! box) {
return 0;
}
return box->p;
}
extern int m_d_box_period_do(double _Complex center, double radius, int maxperiod) {
m_d_box_period_t *box = m_d_box_period_new(center, radius);
if (! box) {
return 0;
}
int period = 0;
for (int i = 0; i < maxperiod; ++i) {
if (m_d_box_period_have_period(box)) {
period = m_d_box_period_get_period(box);
break;
}
if (! m_d_box_period_step(box)) {
break;
}
}
m_d_box_period_delete(box);
return period;
}
/* -----------http://code.mathr.co.uk/mandelbrot-numerics/blob_plain/HEAD:/c/lib/m_r_box_period.c -----------------------*/
static void cross_r(mpfr_t out, const mpc_t a, const mpc_t b, mpfr_t t) {
mpfr_mul(out, mpc_imagref(a), mpc_realref(b), MPFR_RNDN);
mpfr_mul(t, mpc_realref(a), mpc_imagref(b), MPFR_RNDN);
mpfr_sub(out, out, t, MPFR_RNDN);
}
static bool crosses_positive_real_axis_r(const mpc_t a, const mpc_t b, mpc_t d, mpfr_t t1, mpfr_t t2) {
if (mpfr_sgn(mpc_imagref(a)) != mpfr_sgn(mpc_imagref(b))) {
// d = b - a;
mpc_sub(d, b, a, MPC_RNDNN);
// s = sgn(cimag(d));
int s = mpfr_sgn(mpc_imagref(d));
// t = sgn(cross(d, a));
cross_r(t1, d, a, t2);
int t = mpfr_sgn(t1);
return s == t;
}
return false;
}
static bool surrounds_origin_r(const mpc_t a, const mpc_t b, const mpc_t c, const mpc_t d, mpc_t e, mpfr_t t1, mpfr_t t2) {
return odd
( crosses_positive_real_axis_r(a, b, e, t1, t2)
+ crosses_positive_real_axis_r(b, c, e, t1, t2)
+ crosses_positive_real_axis_r(c, d, e, t1, t2)
+ crosses_positive_real_axis_r(d, a, e, t1, t2)
);
}
typedef struct m_r_box_period {
mpc_t c[4];
mpc_t z[4];
int p;
mpc_t e;
mpfr_t t1;
mpfr_t t2;
} m_r_box_period_t;
extern m_r_box_period_t *m_r_box_period_new(const mpc_t center, const mpfr_t radius) {
m_r_box_period_t *box = (m_r_box_period_t *) malloc(sizeof(*box));
if (! box) {
return 0;
}
// prec
mpfr_prec_t precr, preci, prec;
mpc_get_prec2(&precr, &preci, center);
prec = precr > preci ? precr : preci;
// init
for (int i = 0; i < 4; ++i) {
mpc_init2(box->c[i], prec);
mpc_init2(box->z[i], prec);
}
mpc_init2(box->e, prec);
mpfr_init2(box->t1, prec);
mpfr_init2(box->t2, prec);
// box
mpfr_sub(mpc_realref(box->c[0]), mpc_realref(center), radius, MPFR_RNDN);
mpfr_sub(mpc_imagref(box->c[0]), mpc_imagref(center), radius, MPFR_RNDN);
mpfr_add(mpc_realref(box->c[1]), mpc_realref(center), radius, MPFR_RNDN);
mpfr_sub(mpc_imagref(box->c[1]), mpc_imagref(center), radius, MPFR_RNDN);
mpfr_add(mpc_realref(box->c[2]), mpc_realref(center), radius, MPFR_RNDN);
mpfr_add(mpc_imagref(box->c[2]), mpc_imagref(center), radius, MPFR_RNDN);
mpfr_sub(mpc_realref(box->c[3]), mpc_realref(center), radius, MPFR_RNDN);
mpfr_add(mpc_imagref(box->c[3]), mpc_imagref(center), radius, MPFR_RNDN);
mpc_set(box->z[0], box->c[0], MPC_RNDNN);
mpc_set(box->z[1], box->c[1], MPC_RNDNN);
mpc_set(box->z[2], box->c[2], MPC_RNDNN);
mpc_set(box->z[3], box->c[3], MPC_RNDNN);
box->p = 1;
return box;
}
extern void m_r_box_period_delete(m_r_box_period_t *box) {
if (box) {
for (int i = 0; i < 4; ++i) {
mpc_clear(box->c[i]);
mpc_clear(box->z[i]);
}
mpc_clear(box->e);
mpfr_clear(box->t1);
mpfr_clear(box->t2);
free(box);
}
}
extern bool m_r_box_period_step(m_r_box_period_t *box) {
if (! box) {
return false;
}
bool ok = true;
for (int i = 0; i < 4; ++i) {
// box->z[i] = box->z[i] * box->z[i] + box->c[i];
mpc_sqr(box->z[i], box->z[i], MPC_RNDNN);
mpc_add(box->z[i], box->z[i], box->c[i], MPC_RNDNN);
ok = ok && mpfr_number_p(mpc_realref(box->z[i])) && mpfr_number_p(mpc_imagref(box->z[i]));
}
box->p = box->p + 1;
return ok;
}
extern bool m_r_box_period_have_period(const m_r_box_period_t *box) {
if (! box) {
return true;
}
m_r_box_period_t *ubox = (m_r_box_period_t *) box; // const cast
return surrounds_origin_r(box->z[0], box->z[1], box->z[2], box->z[3], ubox->e, ubox->t1, ubox->t2);
}
extern int m_r_box_period_get_period(const m_r_box_period_t *box) {
if (! box) {
return 0;
}
return box->p;
}
extern int m_r_box_period_do(const mpc_t center, const mpfr_t radius, int maxperiod) {
m_r_box_period_t *box = m_r_box_period_new(center, radius);
if (! box) {
return 0;
}
int period = 0;
for (int i = 0; i < maxperiod; ++i) {
if (m_r_box_period_have_period(box)) {
period = m_r_box_period_get_period(box);
break;
}
if (! m_r_box_period_step(box)) {
break;
}
}
m_r_box_period_delete(box);
return period;
}
/*--------------- */
/*
c:0.37496784+%i*0.21687214;
./a.out 100 0.37496784 0.21687214 1.0 20
./a.out 200 -1.121550281113895 +0.265176187855967 0.005 40
so radius = domain size
*/
static void usage(const char *progname) {
fprintf
( stderr
, "usage: %s precision center-re center-im radius maxperiod\n"
, progname
);
}
/* ========================= mAIN =========================== */
extern int main(int argc, char **argv) {
if (argc != 6) {
usage(argv[0]);
return 1;
}
bool native = true;
int bits = 0;
if (! arg_precision(argv[1], &native, &bits)) { return 1; }
if (native) {
double cre = 0;
double cim = 0;
double radius = 0;
int maxperiod = 0;
if (! arg_double(argv[2], &cre)) { return 1; }
if (! arg_double(argv[3], &cim)) { return 1; }
if (! arg_double(argv[4], &radius)) { return 1; }
if (! arg_int(argv[5], &maxperiod)) { return 1; }
int period = m_d_box_period_do(cre + I * cim, radius, maxperiod);
if (period > 0) {
printf("%d\n", period);
return 0;
}
} else {
mpc_t center;
mpfr_t radius;
int maxperiod = 0;
mpc_init2(center, bits);
mpfr_init2(radius, bits);
if (! arg_mpc(argv[2], argv[3], center)) { return 1; }
if (! arg_mpfr(argv[4], radius)) { return 1; }
if (! arg_int(argv[5], &maxperiod)) { return 1; }
int period = m_r_box_period_do(center, radius, maxperiod);
if (period > 0) {
printf("%d\n", period);
}
mpc_clear(center);
mpfr_clear(radius);
return period <= 0;
}
return 1;
}
m-interior
Interior coordinates in the Mandelbrot set
Steps: C is fixed throughout this process - it determines the pixel we want to colour.
The first step is to find a special z (maybe call it w) such that p iterations of z to z^2 + c starting from w, gets you back to w. This is the limit cycle attractor of c. This is done by m_d_attractor, using Newton's method to solve f_c^p(z) - z = 0.
Then to find the interior coordinate for c, take your w, and iterate it p times, calculating the derivative w.r.t. z:
z = w; dz = 1; for (int i = 0; i < p; ++i)
dz = 2 * z * dz z = z * z + c
then the interior coordinate is simply dz after the loop. if |dz| < 1 then c is interior to a component of period p
you can colour pixels based on dz (eg angle -> hue, radius -> saturation)
for highlighting the edge you can optionally use the w to find the interior distance estimate (m_d_interior_de).
Description
- from math.stackexchange[6]
- blog [7]
- "traced boundaries using Newton's method in two variables"
- theory
an algorithm to find points on the boundary of the Mandelbrot set, given a particular hyperbolic component and the desired internal angle. It involves Newton's method in two complex variables to solve system of 2 equations:
where:
- F is function ( complex quadratic polynomial)
- is iterated polynomial
- p is the period of the target component
- with |r|≤1.
- θ is the desired internal angle.
- First equation describes periodic point
- second equation describes attractive periodic point ( magnitude r of multiplier b is not grater then 1 )
The resulting c is the coordinates of the point on the boundary. It can also be modified to find points in the interior, simply set b=re2πiθ with |r|≤1.
The algorithm for finding numerically interior coordinate b by Claude:
- When c is outside the Mandelbrot set, give up now;
- For each period p, starting from 1 and increasing:
- Find z0 such that Fp(z0,c)=z0 using Newton's method in one complex variable;
- Find b by evaluating first derivative with respect to z at z0;
- If |b|≤1 then return b, otherwise continue with the next p.
usage
Use without parameters:
m-interior
gives usage
usage: ./m-interior precision z-guess-re z-guess-im c-guess-re c-guess-im interior-r interior-t period maxsteps
| parameter | variable | description |
|---|---|---|
| precision | int bits | number of binary digits = width of significant = precision. Here one can use :
|
| z-guess-re | double zre | real part of the initial guess z_0 for Newton method, use z = 0 |
| z-guess-im | double zim | |
| c-guess-re | double cre | real part of the initial guess c_0 for Newton method, use nucleus of given hyperbolic component |
| c-guess-im | double cim | imaginary part of c_0 |
| interior-r | double ir | Example |
| interior-t | double it | Example |
| period | int period | Period of given hyperbolic component |
| maxsteps | int maxsteps | Example |
z-guess = z-guess-re+z-guess-im*I c-guess = c-guess-re + c-guess=im*I
Output:
- point c with given internal coordinate from hyperbolic componenet described by period and nuceus
- periodic point z (wucleus)
Example :
./a.out double 0 0 0 0 1 0 1 100 5.0000000000000000e-01 0.0000000000000000e+00 2.5000000000000000e-01 0.0000000000000000e+00
General algorithm:
- choose period
- compute / choose center c from period = initial aproximation
- compute size of component with center c. Compute precision from size
- choose t = p/q and r
- compute
code
Program m-interior from bin directory
Source code :
- mandelbrot-numerics/c/bin/ m-interior.c
- mandelbrot-numerics/c/lib/m_d_interior.c
- mandelbrot-numerics/c/lib/m_r_interior.c
Functions:
- m_d_interior(&z, &c, zre + I * zim, cre + I * cim, ir * cexp(I * twopi * it), period, maxsteps);
- m_r_interior(z, c, z, c, interior, period, maxsteps);
#include <mandelbrot-numerics.h>
#include "m_d_util.h"
extern m_newton m_d_interior_step(double _Complex *z_out, double _Complex *c_out, double _Complex z_guess, double _Complex c_guess, double _Complex interior, int period) {
double _Complex c = c_guess;
double _Complex z = z_guess;
double _Complex dz = 1;
double _Complex dc = 0;
double _Complex dzdz = 0;
double _Complex dcdz = 0;
for (int p = 0; p < period; ++p) {
dcdz = 2 * (z * dcdz + dc * dz);
dzdz = 2 * (z * dzdz + dz * dz);
dc = 2 * z * dc + 1;
dz = 2 * z * dz;
z = z * z + c;
}
double _Complex det = (dz - 1) * dcdz - dc * dzdz;
double _Complex z_new = z_guess - (dcdz * (z - z_guess) - dc * (dz - interior)) / det;
double _Complex c_new = c_guess - ((dz - 1) * (dz - interior) - dzdz * (z - z_guess)) / det;
if (cisfinite(z_new) && cisfinite(c_new)) {
*z_out = z_new;
*c_out = c_new;
if (cabs2(z_new - z_guess) <= epsilon2 && cabs2(c_new - c_guess) <= epsilon2) {
return m_converged;
} else {
return m_stepped;
}
} else {
*z_out = z_guess;
*c_out = c_guess;
return m_failed;
}
}
extern m_newton m_d_interior(double _Complex *z_out, double _Complex *c_out, double _Complex z_guess, double _Complex c_guess, double _Complex interior, int period, int maxsteps) {
m_newton result = m_failed;
double _Complex z = z_guess;
double _Complex c = c_guess;
for (int i = 0; i < maxsteps; ++i) {
if (m_stepped != (result = m_d_interior_step(&z, &c, z, c, interior, period))) {
break;
}
}
*z_out = z;
*c_out = c;
return result;
}
m-interior-de
description[8]
m-attractor
to find a special z (maybe call it w) such that p iterations of z to z^2 + c starting from w, gets you back to w. This is the limit cycle attractor of c. It is done using Newton's method to solve f_c^p(z) - z = 0.
usage: %s precision z-guess-re z-guess-im c-re c-im period maxsteps
Finds one periodic z point ( point on dynamical plane ) near z-guess
- for :
- period
- c= c-re + c-im* i
- using Newton method with :
- z-guess = z-guess-re + z-guess-im* i ( initial aproximation of the root)
- maxima number of steps = maxsteps
- using number with width of significant = precision. Here one can use :
- double or 53
- positive integer = number of bits for MPFR
./m-attractor double 0 0 -0.965 0.085 2 100
or
./m-attractor 53 0 0 -0.965 0.085 2 100
result :
-2.7669310528133408e-02 -8.9979332165608591e-02
The precision is set manually in m-attractor to let user experiment.
m-exray-in
Parameter external ray:[9]
- traced inward ( from infinity to the boundary )
- using Newton method
When tracing inwards, one peels off the most-significant bit (aka angle doubling) each time the ray crosses a dwell band (integer part of normalized iteration count increases by 1).
binaries
~/mandelbrot-numerics/c/bin$ ./m-exray-in usage: ./m-exray-in precision angle sharpness maxsteps
./m-exray-in double 1/3 4 200
Code
Source code:
- c/bin/m-exray-in.c = program showing usage of the library function
- c/lib/m_d_exray_in.c = double ( machine double precision ) version of procedure
- c/lib/m_r_exray_in.c = mpfr version of procedure = (dynamically changed as necessary) precision
variables :
- native ( if true then use double= native precision)
- precision (can be double , see arg_precision )
double version :
m_newton m_d_exray_in_step(m_d_exray_in *ray, int maxsteps) {
if (ray->j >= ray->sharpness) {
mpq_mul_2exp(ray->angle, ray->angle, 1);
if (mpq_cmp_ui(ray->angle, 1, 1) >= 0) {
mpq_sub(ray->angle, ray->angle, ray->one);
}
ray->k = ray->k + 1;
ray->j = 0;
}
double r = pow(ray->er, pow(0.5, (ray->j + 0.5) / ray->sharpness));
double a = twopi * mpq_get_d(ray->angle);
double _Complex target = r * (cos(a) + I * sin(a));
double _Complex c = ray->c;
for (int i = 0; i < maxsteps; ++i) {
double _Complex z = 0;
double _Complex dc = 0;
for (int p = 0; p <= ray->k; ++p) {
dc = 2 * z * dc + 1;
z = z * z + c;
}
double _Complex c_new = c - (z - target) / dc;
double d2 = cabs2(c_new - c);
if (cisfinite(c_new)) {
c = c_new;
} else {
break;
}
if (d2 <= epsilon2) {
break;
}
}
ray->j = ray->j + 1;
double d2 = cabs2(c - ray->c);
if (d2 <= epsilon2) {
ray->c = c;
return m_converged;
}
if (cisfinite(c)) {
ray->c = c;
return m_stepped;
} else {
return m_failed;
}
}
mpfr version :
/*
it is a c console program which
- computes external parameter ray
- for complex quadratic polynomial fc(z) = z^2+c
- uses arbitrary precision ( mpfr) with dynamic precision adjustment
- uses Newton method ( described by T Kawahira) http://www.math.nagoya-u.ac.jp/~kawahira/programs/mandel-exray.pdf
gcc -o rayin e.c -std=c99 -Wall -Wextra -pedantic -lmpfr -lgmp -lm
./rayin 1/3 25
./rayin 1/3 25 >ray13.txt
./rayin 1/3 25 | ./rescale 53 53 -0.75 0 1.5 0 >rray13.txt
program uses the code by Claude Heiland-Allen
from https://gitorious.org/maximus/book/
" ray_in computes 4 points per dwell band, and ray_out currently computes 16.
Moreover ray_in has dynamic precision adjustment and
ray_out doesn't (so you need a high precision to get through the thin
gaps) - fixing both of these is on my mental todo list. ray_out will
always be slower though, as it needs to compute extra points when
crossing dwell bands to accumulate angle bits (and to work correctly)."
What algorithm do you use for drawing external ray ?
"essentially the Newton's method one in
http://www.math.nagoya-u.ac.jp/~kawahira/programs/mandel-exray.pdf
precision is automatic, effectively it checks how close dwell bands are
together and uses higher precision when they are narrow and lower
precision when they are wide. in general precision will increase along
the ray as it gets closer to the boundary. "
"periodic rays stop near the landing point at the current zoom level,
manually retrace if you zoom in and find the gap annoying. tracing
periodic rays is a lot slower than tracing preperiodic rays, especially
if you zoom in to the cusp - suggestions welcome for improvements here
(perhaps a larger radius than a single pixel for landing point nearness
threshold?). "
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <gmp.h>
#include <mpfr.h> // arbitrary precision
const float pif = 3.14159265358979323846264338327950288419716939937510f;
const double pi = 3.14159265358979323846264338327950288419716939937510;
const long double pil = 3.14159265358979323846264338327950288419716939937510l;
struct mandelbrot_external_ray_in {
mpq_t angle;
mpq_t one;
unsigned int sharpness; // number of steps to take within each dwell band
unsigned int precision; // delta needs this many bits of effective precision
unsigned int accuracy; // epsilon is scaled relative to magnitude of delta
double escape_radius;
mpfr_t epsilon2;
mpfr_t cx;
mpfr_t cy;
unsigned int j;
unsigned int k;
// temporaries
mpfr_t zx, zy, dzx, dzy, ux, uy, vx, vy, ccx, ccy, cccx, cccy;
};
// new : allocates memory, inits and sets variables
// input angle = external angle in turns
extern struct mandelbrot_external_ray_in *mandelbrot_external_ray_in_new(mpq_t angle) {
struct mandelbrot_external_ray_in *r = malloc(sizeof(struct mandelbrot_external_ray_in));
mpq_init(r->angle);
mpq_set(r->angle, angle);
mpq_init(r->one);
mpq_set_ui(r->one, 1, 1);
r->sharpness = 4;
r->precision = 4;
r->accuracy = 4;
r->escape_radius = 65536.0;
mpfr_init2(r->epsilon2, 53);
mpfr_set_ui(r->epsilon2, 1, GMP_RNDN);
// external angle in radions
double a = 2.0 * pi * mpq_get_d(r->angle);
// initial value c =
mpfr_init2(r->cx, 53);
mpfr_init2(r->cy, 53);
mpfr_set_d(r->cx, r->escape_radius * cos(a), GMP_RNDN);
mpfr_set_d(r->cy, r->escape_radius * sin(a), GMP_RNDN);
r->k = 0;
r->j = 0;
// initialize temporaries
mpfr_inits2(53, r->zx, r->zy, r->dzx, r->dzy, r->ux, r->uy, r->vx, r->vy, r->ccx, r->ccy, r->cccx, r->cccy, (mpfr_ptr) 0);
return r;
}
// delete
extern void mandelbrot_external_ray_in_delete(struct mandelbrot_external_ray_in *r) {
mpfr_clear(r->epsilon2);
mpfr_clear(r->cx);
mpfr_clear(r->cy);
mpq_clear(r->angle);
mpq_clear(r->one);
mpfr_clears(r->zx, r->zy, r->dzx, r->dzy, r->ux, r->uy, r->vx, r->vy, r->ccx, r->ccy, r->cccx, r->cccy, (mpfr_ptr) 0);
free(r);
}
// step
extern int mandelbrot_external_ray_in_step(struct mandelbrot_external_ray_in *r) {
if (r->j >= r->sharpness) {
mpq_mul_2exp(r->angle, r->angle, 1);
if (mpq_cmp_ui(r->angle, 1, 1) >= 0) {
mpq_sub(r->angle, r->angle, r->one);
}
r->k++;
r->j = 0;
}
// r0 <- er ** ((1/2) ** ((j + 0.5)/sharpness))
// t0 <- r0 cis(2 * pi * angle)
double r0 = pow(r->escape_radius, pow(0.5, (r->j + 0.5) / r->sharpness));
double a0 = 2.0 * pi * mpq_get_d(r->angle);
double t0x = r0 * cos(a0);
double t0y = r0 * sin(a0);
// c <- r->c
mpfr_set(r->ccx, r->cx, GMP_RNDN);
mpfr_set(r->ccy, r->cy, GMP_RNDN);
for (unsigned int i = 0; i < 64; ++i) { // FIXME arbitrary limit
// z <- 0
// dz <- 0
mpfr_set_ui(r->zx, 0, GMP_RNDN);
mpfr_set_ui(r->zy, 0, GMP_RNDN);
mpfr_set_ui(r->dzx, 0, GMP_RNDN);
mpfr_set_ui(r->dzy, 0, GMP_RNDN);
// iterate
for (unsigned int p = 0; p <= r->k; ++p) {
// dz <- 2 z dz + 1
mpfr_mul(r->ux, r->zx, r->dzx, GMP_RNDN);
mpfr_mul(r->uy, r->zy, r->dzy, GMP_RNDN);
mpfr_mul(r->vx, r->zx, r->dzy, GMP_RNDN);
mpfr_mul(r->vy, r->zy, r->dzx, GMP_RNDN);
mpfr_sub(r->dzx, r->ux, r->uy, GMP_RNDN);
mpfr_add(r->dzy, r->vx, r->vy, GMP_RNDN);
mpfr_mul_2ui(r->dzx, r->dzx, 1, GMP_RNDN);
mpfr_mul_2ui(r->dzy, r->dzy, 1, GMP_RNDN);
mpfr_add_ui(r->dzx, r->dzx, 1, GMP_RNDN);
// z <- z^2 + c
mpfr_sqr(r->ux, r->zx, GMP_RNDN);
mpfr_sqr(r->uy, r->zy, GMP_RNDN);
mpfr_sub(r->vx, r->ux, r->uy, GMP_RNDN);
mpfr_mul(r->vy, r->zx, r->zy, GMP_RNDN);
mpfr_mul_2ui(r->vy, r->vy, 1, GMP_RNDN);
mpfr_add(r->zx, r->vx, r->ccx, GMP_RNDN);
mpfr_add(r->zy, r->vy, r->ccy, GMP_RNDN);
}
// c' <- c - (z - t0) / dz
mpfr_sqr(r->ux, r->dzx, GMP_RNDN);
mpfr_sqr(r->uy, r->dzy, GMP_RNDN);
mpfr_add(r->vy, r->ux, r->uy, GMP_RNDN);
mpfr_sub_d(r->zx, r->zx, t0x, GMP_RNDN);
mpfr_sub_d(r->zy, r->zy, t0y, GMP_RNDN);
mpfr_mul(r->ux, r->zx, r->dzx, GMP_RNDN);
mpfr_mul(r->uy, r->zy, r->dzy, GMP_RNDN);
mpfr_add(r->vx, r->ux, r->uy, GMP_RNDN);
mpfr_div(r->ux, r->vx, r->vy, GMP_RNDN);
mpfr_sub(r->cccx, r->ccx, r->ux, GMP_RNDN);
mpfr_mul(r->ux, r->zy, r->dzx, GMP_RNDN);
mpfr_mul(r->uy, r->zx, r->dzy, GMP_RNDN);
mpfr_sub(r->vx, r->ux, r->uy, GMP_RNDN);
mpfr_div(r->uy, r->vx, r->vy, GMP_RNDN);
mpfr_sub(r->cccy, r->ccy, r->uy, GMP_RNDN);
// delta^2 = |c' - c|^2
mpfr_sub(r->ux, r->cccx, r->ccx, GMP_RNDN);
mpfr_sub(r->uy, r->cccy, r->ccy, GMP_RNDN);
mpfr_sqr(r->vx, r->ux, GMP_RNDN);
mpfr_sqr(r->vy, r->uy, GMP_RNDN);
mpfr_add(r->ux, r->vx, r->vy, GMP_RNDN);
// enough_bits = 0 < 2 * prec(eps^2) + exponent eps^2 - 2 * precision
int enough_bits = 0 < 2 * (mpfr_get_prec(r->epsilon2) - r->precision) + mpfr_get_exp(r->epsilon2);
if (enough_bits) {
// converged = delta^2 < eps^2
int converged = mpfr_less_p(r->ux, r->epsilon2);
if (converged) {
// eps^2 <- |c' - r->c|^2 >> (2 * accuracy)
mpfr_sub(r->ux, r->cccx, r->cx, GMP_RNDN);
mpfr_sub(r->uy, r->cccy, r->cy, GMP_RNDN);
mpfr_sqr(r->vx, r->ux, GMP_RNDN);
mpfr_sqr(r->vy, r->uy, GMP_RNDN);
mpfr_add(r->ux, r->vx, r->vy, GMP_RNDN);
mpfr_div_2ui(r->epsilon2, r->ux, 2 * r->accuracy, GMP_RNDN);
// j <- j + 1
r->j = r->j + 1;
// r->c <- c'
mpfr_set(r->cx, r->cccx, GMP_RNDN);
mpfr_set(r->cy, r->cccy, GMP_RNDN);
return 1;
}
} else {
// bump precision
mpfr_prec_t prec = mpfr_get_prec(r->cx) + 32;
mpfr_prec_round(r->cx, prec, GMP_RNDN);
mpfr_prec_round(r->cy, prec, GMP_RNDN);
mpfr_prec_round(r->epsilon2, prec, GMP_RNDN);
mpfr_set_prec(r->ccx, prec);
mpfr_set_prec(r->ccy, prec);
mpfr_set_prec(r->cccx, prec);
mpfr_set_prec(r->cccy, prec);
mpfr_set_prec(r->zx, prec);
mpfr_set_prec(r->zy, prec);
mpfr_set_prec(r->dzx, prec);
mpfr_set_prec(r->dzy, prec);
mpfr_set_prec(r->ux, prec);
mpfr_set_prec(r->uy, prec);
mpfr_set_prec(r->vx, prec);
mpfr_set_prec(r->vy, prec);
i = 0;
}
mpfr_set(r->ccx, r->cccx, GMP_RNDN);
mpfr_set(r->ccy, r->cccy, GMP_RNDN);
}
return 0;
}
// get
extern void mandelbrot_external_ray_in_get(struct mandelbrot_external_ray_in *r, mpfr_t x, mpfr_t y) {
mpfr_set_prec(x, mpfr_get_prec(r->cx));
mpfr_set(x, r->cx, GMP_RNDN);
mpfr_set_prec(y, mpfr_get_prec(r->cy));
mpfr_set(y, r->cy, GMP_RNDN);
}
void usage(const char *progname) {
fprintf(stderr,
"usage: %s angle depth\n"
"outputs space-separated complex numbers on stdout\n"
"example : \n %s 1/3 25\n"
"or \n %s 1/3 25 > r.txt\n",
progname, progname, progname);
}
// needs input
int main(int argc, char **argv) {
// read and check input
if (argc < 3) { usage(argv[0]); return 1; }
mpq_t angle;
mpq_init(angle);
mpq_set_str(angle, argv[1], 0);
mpq_canonicalize(angle);
int depth = atoi(argv[2]);
struct mandelbrot_external_ray_in *ray = mandelbrot_external_ray_in_new(angle);
mpfr_t cre, cim;
mpfr_init2(cre, 53);
mpfr_init2(cim, 53);
// compute and send output
for (int i = 0; i < depth * 4; ++i) {
mandelbrot_external_ray_in_step(ray);
mandelbrot_external_ray_in_get(ray, cre, cim);
// send new c to output
mpfr_out_str(0, 10, 0, cre, GMP_RNDN); putchar(' ');
mpfr_out_str(0, 10, 0, cim, GMP_RNDN); putchar('\n');
}
// clear
mpfr_clear(cre);
mpfr_clear(cim);
mandelbrot_external_ray_in_delete(ray);
mpq_clear(angle);
return 0;
}
m-exray-out
The trick when tracing outwards is to prepend bits when crossing dwell bands, depending if the outer cell was entered from its left or right inner cell. A picture may make it clearer:
Parameter external ray:
- traced outward ( from point c ( from exterior of Mandelbrot set ) to the infinity )
- using Newton method
"there are m_r_exray_out_* functions that can be used to get the external angle by tracing an external ray. but it is O(dwell^2), too slow to be practical beyond a few 1000, and it does not yet have adaptive precision so it cam get stuck in tight gaps between spirals..."
checkin what ray
- crosses given c point
- land on that c point
arguments:
- precision: input string is converted to integer number, in bits "replace double with 1000 to use 1000 bits instead of native 53". It can be "double" string = native precision.
- c-re = real part of complex c
- c-im = imaginary part of complex c
- int sharpness ( replace 8 with 4 to be less sharp, but don't go too low or it may break )
- int maxdwell
- used only for formatting output (" if you have a desired (pre)period, use that to get the angle formatted nicely" )
- preperiod ( int)
- period (int)
usage :
m-exray-out precision c-re c-im sharpness maxdwell preperiod period
Example
m-exray-out double -0.1 0.651 8 10000 100000 1 | tail -n 1
output ( only binary expansion of externala angle):
.00100100100100100100100100100100100100100100100100100100100100100100100100()
or full output:
m-exray-out double -1.7904997268969142e-01 1.0856197533070304e+00 4 20 100 1 -1.7904997268969142e-01 1.0856197533070304e+00 -1.7935443511056054e-01 1.0854961235734493e+00 -1.7969015435633140e-01 1.0853555826931407e+00 -1.8051917357961708e-01 1.0850119514784207e+00 1 -1.8269681168554189e-01 1.0840986080730519e+00 -1.8930978756749961e-01 1.0809967205891908e+00 0 -1.9360134634853554e-01 1.0737664210007076e+00 1 -2.0801776265667046e-01 1.0704315884719302e+00 0 -2.4370145596832851e-01 1.0627226337492655e+00 1 -2.7278498707172455e-01 1.0400463032627758e+00 1 -3.6142246174842857e-01 9.5627327660306660e-01 -4.0875942404913329e-01 9.4318016425218687e-01 -4.5809426255241681e-01 9.9407738931502432e-01 1 -6.0223759082842288e-01 9.3674887784190841e-01 -8.0664626534435835e-01 8.8455840042031386e-01 0 -8.3743553612789834e-01 9.3674304615806725e-01 -8.7287981833135664e-01 9.9952074265609137e-01 -9.1381642842183941e-01 1.0750773818725967e+00 -9.6138941844723436e-01 1.1665050307228815e+00 0 -1.0172147464760770e+00 1.2782611560409487e+00 -1.0836516873794186e+00 1.4168346080502183e+00 -1.1642543320399381e+00 1.5917680433570660e+00 -1.2645279518271537e+00 1.8173272090846146e+00 0 -1.3932089082214374e+00 2.1153654197070240e+00 -1.5644798765083927e+00 2.5204286897782238e+00 -1.8019543103478257e+00 3.0891768094384502e+00 -2.1462162170666716e+00 3.9184694463323830e+00 1 -2.6699272827383060e+00 5.1817748128576184e+00 -3.5099957053533952e+00 7.2066815445348764e+00 -4.9407140183321250e+00 1.0650884836446950e+01 -7.5526171722332034e+00 1.6932133257514206e+01 0 -1.2727799761990893e+01 2.9370322256332429e+01 -2.4030360674257757e+01 5.6528056606204473e+01 -5.1753810887543764e+01 1.2313571132413860e+02 -1.2986129881788275e+02 3.1079020626913712e+02 1 -3.8951035577778663e+02 9.3459826885312373e+02 -1.4412515103402823e+03 3.4614095793299703e+03 -6.8365543576278487e+03 1.6423640211807055e+04 -4.3547867632624519e+04 1.0462387704049867e+05 0 -3.9380510085478675e+05 9.4611788566395245e+05 -5.4017847803638447e+06 1.2977803446720989e+07 -1.2161023621086851e+08 2.9216894171553040e+08 .01010001110101()
Input :
./ray_in ".(0101101011010110101101011010110101100)" 1000
m-feigenbaum
computes c centers of hyperbolic components for period doubling cascade on the real axis ( so imaginary part is 0):
- center for period 1 : c = 0 ( omitted)
- center for period 2 : c = -1
- center for period 2^2= 4 : c = -1.310702641336833008
- ...
- center for period 2^n
./m-feigenbaum
-1.000000000000000000e+00
-1.310702641336833008e+00
-1.381547484432061657e+00
-1.396945359704560685e+00
-1.400253081214782869e+00
-1.400961962944840655e+00
-1.401113804939776664e+00
-1.401146325826946537e+00
-1.401153290849922906e+00
-1.401154782546613964e+00
-1.401155102022467736e+00
-1.401155170444417619e+00
-1.401155185098302614e+00
-1.401155188236698823e+00
-1.401155188908866478e+00
-1.401155189052811778e+00
-1.401155189083657104e+00
-1.401155189090263598e+00
-1.401155189091694675e+00
-1.401155189093319819e+00
-1.401155189093314712e+00
-1.401155189093314712e+00
-1.401155189093314712e+00
-1.401155189093314712e+00
-1.401155189093314712e+00
-1.401155189093314712e+00
-1.401155189093314712e+00
-1.401155189093314712e+00
-1.401155189093314712e+00
m-nearest-roots
prints:
- period + 1
- distance
./m-nearest-roots
5 -6.0077592739339081e-01
9 -1.2345690574077126e+00
17 -1.5948261888043576e+00
33 -1.7912740981919455e+00
65 -1.8940314652359109e+00
129 -1.9466050018630559e+00
257 -1.9731986196121953e+00
513 -1.9865731876029906e+00
1025 -1.9932800441369114e+00
2049 -1.9966383822549216e+00
4097 -1.9983187808738916e+00
8193 -1.9991592878359983e+00
nucleus
/*
console program in c language
based on the code by Claude Heiland-Allen
http://code.mathr.co.uk/mandelbrot-numerics
it computes center ( nucleus) of hyperbolic componnet of Mandelbrot set
using Newton method and double precision
https://en.wikibooks.org/wiki/Fractals/Iterations_in_the_complex_plane/Mandelbrot_set/centers
to compile
gcc m.c -Wall -std=c99 -lm
to run
./a.out
-------------
Newton method converged after 6 steps and near c= ( 0.000000 ;1.000000 ) found nucleus = center = ( -0.1225611668766536, 0.7448617666197442 ) for period = 3
Newton method converged after 5 steps and near c= ( 0.250000 ;0.500000 ) found nucleus = center = ( 0.2822713907669139, 0.5300606175785253 ) for period = 4
Newton method converged after 5 steps and near c= ( 0.250000 ;-0.500000 ) found nucleus = center = ( 0.2822713907669139, -0.5300606175785253 ) for period = 4
Newton method converged after 8 steps and near c= ( 0.300000 ;0.300000 ) found nucleus = center = ( 0.3795135880159238, 0.3349323055974976 ) for period = 5
Newton method converged after 5 steps and near c= ( -0.122561 ;0.844862 ) found nucleus = center = ( -0.1134186559494366, 0.8605694725015731 ) for period = 6
Newton method converged after 7 steps and near c= ( -1.250000 ;0.250000 ) found nucleus = center = ( -1.1380006666509646, 0.2403324012620983 ) for period = 6
Newton method converged after 35 steps and near c= ( -3.250000 ;0.250000 ) found nucleus = center = ( -1.9667732163929286, -0.0000000000000000 ) for period = 6
compare
https://gitlab.com/adammajewski/cpp-mandelbrot-center-by-knighty
https://gitlab.com/adammajewski/lawrence
https://gitlab.com/adammajewski/mandelbrot-numerics-nucleus
*/
#include <complex.h>
#include <math.h>
#include <stdbool.h>
#include <stdint.h>
#include <stdlib.h>
#include <stdio.h> //
// from mandelbrot-numerics.h
enum m_newton { m_failed, m_stepped, m_converged };
typedef enum m_newton m_newton;
// from m_d_util.h
static inline bool cisfinite(double _Complex z) {
return isfinite(creal(z)) && isfinite(cimag(z));
}
static inline double cabs2(double _Complex z) {
return creal(z) * creal(z) + cimag(z) * cimag(z);
}
// last . takeWhile (\x -> 2 /= 2 + x) . iterate (/2) $ 1 :: Double
static const double epsilon = 4.440892098500626e-16;
// epsilon^2
static const double epsilon2 = 1.9721522630525295e-31;
int PrintResult(int iResult, double _Complex c_guess, double _Complex nucleus, int period, int steps)
{
static char* sResult;
switch (iResult){
case 0 : sResult = "failed"; break;
case 1 : sResult = "stepped"; break;
case 2 : sResult = "converged"; break;
default : sResult = "unknown";
}
printf("Newton method %s after %d steps and near c= ( %f ;%f ) found nucleus = center = ( %.16f, %.16f ) for period = %d \n ", sResult, steps, creal(c_guess), cimag(c_guess), creal(nucleus), cimag(nucleus), period );
return 0;
}
// ----------------------- from m_d_nucleus.c -------------------------------------------------
// nucleus = center of hyperbolic componnet of Mandelbrot set
// https://en.wikibooks.org/wiki/Fractals/Mathematics/Newton_method#center
//
extern m_newton m_d_nucleus_step(double _Complex *c_out, double _Complex c_guess, int period) {
double _Complex z = 0;
double _Complex dc = 0;
for (int i = 0; i < period; ++i) {
dc = 2 * z * dc + 1;
z = z * z + c_guess;
}
if (cabs2(dc) <= epsilon2) {
*c_out = c_guess;
return m_converged;
}
double _Complex c_new = c_guess - z / dc;
double _Complex d = c_new - c_guess;
if (cabs2(d) <= epsilon2) {
*c_out = c_new;
return m_converged;
}
if (cisfinite(d)) {
*c_out = c_new;
return m_stepped;
} else {
*c_out = c_guess;
return m_failed;
}
}
// compute nucleus using double precision and Newton method
extern m_newton m_d_nucleus(double _Complex *c_out, double _Complex c_guess, int period, int maxsteps) {
m_newton result = m_failed;
double _Complex c = c_guess;
int i;
for (i = 0; i < maxsteps; ++i) {
if (m_stepped != (result = m_d_nucleus_step(&c, c, period))) {
break;
}
}
*c_out = c;
PrintResult(result,c_guess, c , period, i);
return result;
}
/* ==================== main ================================================================================================*/
int main() {
double _Complex c3, c4a, c4b, c5, c3c2, c2c3;
m_d_nucleus(&c3, 0 + I * 1, 3, 64);
m_d_nucleus(&c4a, 0.25 + 0.5 * I, 4, 64);
m_d_nucleus(&c4b, 0.25 - 0.5 * I, 4, 64);
m_d_nucleus(&c5, 0.3 + 0.3 * I, 5, 64);
m_d_nucleus(&c3c2, c3 + I * 0.1, 6, 64);
m_d_nucleus(&c2c3, -1 - 0.25 + 0.25 * I, 6, 64);
m_d_nucleus(&c2c3, -3 - 0.25 + 0.25 * I, 6, 64);
return 0;
}
Images
- Wakes
 Wakes near the period 1 continent
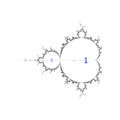
Wakes near the period 1 continent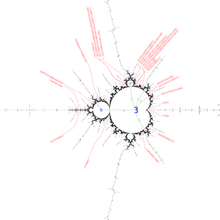 Wakes near the period 3 island
Wakes near the period 3 island Wakes along the main antenna
Wakes along the main antenna
 Escape route 1/2
Escape route 1/2
References
- ↑ stackoverflow question how-to-permanently-set-path-on-linux
- ↑ math.stackexchange question: perfect-circles-in-the-mandelbrot-set
- ↑ atom_domain_size_estimation by Claude Heiland-Allen
- ↑ deriving_the_size_estimate by Claude Heiland-Allen
- ↑ on_the_precision_required_for_size_estimates by Claude Heiland-Allen
- ↑ math.stackexchange question test-for-membership-in-mandelbrot-bulb-of-period-n/1151953#1151953
- ↑ interior_coordinates_in_the_mandelbrot_set
- ↑ practical_interior_distance_rendering
- ↑ mathoverflow question: algorithm-for-computing-external-angles-for-the-mandelbrot-set