Name

• Parabolic chessboard = parabolic checkerboard
• zeros of qn - use only interior of Filled Julia set

Algorithm

Star = Parabolic critical orbit with arms in different colors

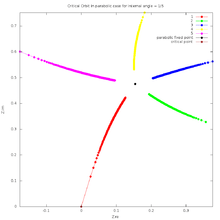
Color depends on:

• sign of imaginary part of numericaly aproximated Fatou coordinate (numerical explanation )
• position of ${\displaystyle z_{\infty }}$ under ${\displaystyle f^{p}}$ in relation to one arm of critical orbit star: above or below ( geometric explanation)

Attracting ( critical orbit) and repelling axes ( external rays landing on the parabolic fixed point ) divide niegbourhood of fixed point intio sectors

How to compute preimages of critical point ?

• (a,b)
• (aa, ab)
• (aaa,aab )
• (aaaa, aaab )
• (aaaaa, aaaab )

dictionary

• The chessboard is the name of this decomposition of A into a graph and boxes
• the chessboard graph
• the chessboard boxes :" The connected components of its complement in A are called the chessboard boxes (in an actual chessboard they are called squares but here they have infinitely many corners and not just four). " ^[1]
• the two principal or main chessboard boxes

description

"A nice way to visualize the extended Fatou coordinates is to make use of the parabolic graph and chessboard." ^[2]

Color points according to :^[3]

• the integer part of Fatou coordinate
• the sign of imaginary part

Corners of the chessboard ( where four tiles meet ) are precritical points ^[4]

${\displaystyle \bigcup _{n=0}^{n\geq 0}f^{-n}(z_{cr})}$

or

${\displaystyle \{z:f^{n}(z)=z_{cr}\}}$

"each yellow tile biholomorphically maps to the upper half plane, and each blue tile biholomorphically maps to the lower half plane under ${\displaystyle \psi _{att}}$. The pre-critical points of ${\displaystyle z+z^{2}}$ or equivalently the critical points of ${\displaystyle \psi _{att}}$ are located where four tiles meet"^[5]

Images

Click on the images to see the code and descriptions on the Commons !

• on the real slice of Mandelbrot set
• 
  on the cusp of main cardioid
• 
• 
  from main cardioid to period 2
• 
  between period 2 and 4 along 1/2 ray

• on the boundary of main cardioid of Mandelbrot set
• 
  0/1 = 1/1
• 
• 
  1/2
• 
  1/3

• other polynomials
• 
  various number of star branches

• orbits inside sepals
• 
  0/1 = 1/1
• 
  invariant curves inside main boxes
• 

Examples :

• Tiles: Tessellation of the Interior of Filled Julia Sets by T Kawahira^[6]
• coloured califlower by A Cheritat ^[7]

code

For the internal angle 0/1 and 1/2 critical orbit is on the real line ( Im(z) = 0). It is easy to compute parabolic chesboard because one have to check only imaginary part of z. For other cases it is not so easy

  // in function uint mndlbrot::esctime(double x, double y)
  if (b == 0.0 && !drawmode && sign < 0
      && (a == 0.25 || a == -0.75)) return parabolic(x, y);
 // uint mndlbrot::parabolic(double x, double y)
 if (Zx>=0 && Zx <= 0.5 && (Zy > 0 ? Zy : -Zy)<= 0.5 - Zx) 
            { if (Zy>0) data[i]=200; // show petal
                     else data[i]=150;}

reset
f(x,y)=  x>=0 && x<=0.5 &&  (y > 0 ? y : -y) <= 0.5 - x
unset colorbox
set isosample 300, 300
set xlabel 'x'
set ylabel 'y'
set sample 300
set pm3d map
splot [-2:2] [-2:2] f(x,y)

  // in function uint mndlbrot::esctime(double x, double y)
  if (b == 0.0 && !drawmode && sign < 0
      && (a == 0.25 || a == -0.75)) return parabolic(x, y);
 // uint mndlbrot::parabolic(double x, double y)
  if (A < 0 && x >= -0.5 && x <= 0 && (y > 0 ? y : -y) <= 0.3 + 0.6*x)
      {  if (j & 1) return (y > 0 ? 65282u : 65290u);
         else return (y > 0 ? 65281u : 65289u);
      }

See also

• Checkerboard in Hyperbolic tilings by User:Tamfang : images and Python code
• https://plus.google.com/110803890168343196795/posts/Eun6pZVkkmA
• shadertoy: Orbit trapped julia Created by maeln in 2016-Jan-19
• Holomorphic checkerboard by etale_cohomology
• Sepals of cauliflower
• wikipedia :Zebra striping in computer graphics

references

1. ↑ Near parabolic renormalization for unisingular holomorphic maps by Arnaud Cheritat
2. ↑ About Inou and Shishikura’s near parabolic renormalization by Arnaud Cheritat
3. ↑ Applications of near-parabolic renormalization by Mitsuhiro Shishikura
4. ↑ Complex Dynamical Systems by Robert L. Devaney, page
5. ↑ Antiholomorphic Dynamics: Topology of Parameter Spaces and Discontinuity of Straightening by Sabyasachi Mukherjee
6. ↑ tiles by T Kawahira
7. ↑ checkerboards by A Cheritat
8. ↑ commons:Category:Fractals created with Mandel
9. ↑ Program Mandel by Wolf Jung
10. ↑ Program Mandel by Wolf Jung