Wiener–Araya graph
The Wiener–Araya graph is, in graph theory, a graph on 42 vertices with 67 edges. It is hypohamiltonian, which means that it does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from it is Hamiltonian. It is also planar.
| Wiener-Araya graph | |
|---|---|
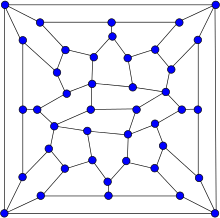 | |
| Vertices | 42 |
| Edges | 67 |
| Radius | 5 |
| Diameter | 7 |
| Girth | 4 |
| Automorphisms | 2 |
| Chromatic number | 3 |
| Chromatic index | 4 |
| Properties | Hypohamiltonian Planar |
| Table of graphs and parameters | |
History
Hypohamiltonian graphs were first studied by Sousselier in Problèmes plaisants et délectables (1963).[1] In 1967, Lindgren builds an infinite sequence of hypohamiltonian graphs.[2] He first cites Gaudin, Herz and Rossi,[3] then Busacker and Saaty[4] as pioneers on this topic.
From the start, the smallest hypohamiltonian graph is known: the Petersen graph. However, the hunt for the smallest planar hypohamiltonian graph continues. This question was first raised by Václav Chvátal in 1973.[5] The answer is provided in 1976 by Carsten Thomassen, who exhibits a 105-vertices construction, the 105-Thomassen graph.[6] In 1979, Hatzel improves this result with a planar hypohamiltonian graph on 57 vertices : the Hatzel graph.[7] This bound is lowered in 2007 by the 48-Zamfirescu graph.[8]
In 2009, a graph built by Gábor Wiener and Makoto Araya becomes (with its 42 vertices) the smallest planar hypohamiltonian graph known.[9][10] In their paper, Wiener and Araya conjecture that their graph's is optimal arguing that its order (42) appears to be the answer to The Ultimate Question of Life, the Universe, and Everything from The Hitchhiker's Guide to the Galaxy, a Douglas Adams novel.
References
- Sousselier, R. (1963), Problème no. 29: Le cercle des irascibles, 7, Rev. Franç. Rech. Opérationnelle, pp. 405–406
- Lindgren, W. F. (1967), "An infinite class of hypohamiltonian graphs", American Mathematical Monthly, 74: 1087–1089, doi:10.2307/2313617, MR 0224501
- Gaudin, T.; Herz, P.; Rossi (1964), "Solution du problème No. 29", Rev. Franç. Rech. Opérationnelle (in French), 8: 214–218
- Busacker, R. G.; Saaty, T. L. (1965), Finite Graphs and Networks
- Chvátal, V. (1973), "Flip-flops in hypo-Hamiltonian graphs", Canadian Mathematical Bulletin, 16: 33–41, doi:10.4153/cmb-1973-008-9, MR 0371722
- Thomassen, Carsten (1976), "Planar and infinite hypohamiltonian and hypotraceable graphs", Discrete Mathematics, 14 (4): 377–389, doi:10.1016/0012-365x(76)90071-6, MR 0422086
- Hatzel, Wolfgang (1979), "Ein planarer hypohamiltonscher Graph mit 57 Knoten", Mathematische Annalen (in German), 243 (3): 213–216, doi:10.1007/BF01424541, MR 0548801
- Zamfirescu, Carol T.; Zamfirescu, Tudor I. (2007), "A planar hypohamiltonian graph with 48 vertices", Journal of Graph Theory, 55 (4): 338–342, doi:10.1002/jgt.20241, MR 2336805
- Wiener, Gábor; Araya, Makoto (April 20, 2009), The ultimate question, arXiv:0904.3012, Bibcode:2009arXiv0904.3012W.
- Wiener, Gábor; Araya, Makoto (2011), "On planar hypohamiltonian graphs", Journal of Graph Theory, 67 (1): 55–68, doi:10.1002/jgt.20513, MR 2809563.