Suffix automaton

In computer science, a suffix automaton is the smallest partial deterministic finite automaton that recognizes the set of suffixes of a given string. The state graph of the suffix automaton is called the directed acyclic word graph (DAWG). The term DAWG is also sometimes used for any deterministic acyclic finite state automaton. The term suffix automaton is also sometimes used for any automaton recognizing suffixes of a text.

For example, the suffix automaton of the string "suffix" accepts the strings "suffix", "uffix", "ffix", "fix", "ix", "x" and the empty string. The automaton can be thought of as a compressed form of the trie of all suffixes of a text. It can be constructed in linear time in the length of the string.[1] For a string S of length at least 2, the suffix automaton has at most states and at most transitions.[1]

Suffix automata have applications in approximate string matching.[2]

Properties
The suffix automaton of abbab. The primary edges are in black, secondary edges are in gray and suffix pointers are in red. Accepting states are marked by a double circle.

The states of the suffix automaton correspond to classes of end-position equivalent strings, defined as follows:

Suppose we have a string S. We say that substrings x and y of S are end-position equivalent if the sets of all end positions of occurrences of x and y in S are the same. This relation partitions the substrings of S into equivalence classes which are in a one-to-one correspondence with the states of the suffix automaton. The strings in the class of a node v are spelled out by paths from the source to v.

We call the longest string in an equivalence class of a state v the representative of that class, and it is spelled out by the longest path from the source to v. The automaton has one sink state, which represents the whole string S.

There is an edge labelled with a from the state represented by x to the state represented by y if and only if xa is end-position equivalent with y. Each edge of the suffix automaton is either primary or secondary. An edge labelled with character a from the state represented by x is primary if and only if xa is the representative of an equivalence class. The distinction between primary and secondary edges is important in the construction of the automaton and the analysis of the size of the automaton.[1] For practical applications the automaton is also usually augmented with suffix pointers, which point from a state represented by x to the state represented by the longest proper suffix of x that represents a class.

Applications

The suffix automaton of S can be used to efficiently decide whether a query string Q is a substring of S. This is true if and only if there exists a path starting from the source of the automaton that spells Q. This works because every substring of S is a prefix of a suffix of S.

When combined with dynamic programming, the automaton can be used to answer many interesting questions about S. For example, the number of distinct substrings of S is equal to the number of distinct paths in the automaton starting from the source, which can be counted using dynamic programming on the automaton. The number of occurrences of any substring Q of S can be counted by finding the state v such that a path from the source to v spells Q and then counting the number of paths from v to the sink state of the automaton.

Relationships with other suffix structures
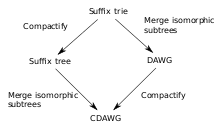
Relationship of the suffix trie, suffix tree, DAWG and CDAWG.[3]

The directed acyclic word graph (DAWG) of S can be obtained by taking the trie of suffixes of S and merging all isomorphic subtrees. The DAWG also has another deep connection with the suffix tree of S: The suffix pointers of the DAWG of S form a tree which is identical to the suffix tree of the reverse of S.

Replacing all non-branching paths of the DAWG with a single edge gives a data structure that is called the compact DAWG, or the CDAWG of S. The CDAWG is identical to the DAG obtained by merging all isomorphic subtrees of the suffix tree of S.

See also

References
  1. Blumer, A.; Blumer, J.; Haussler, D. (1985), "The smallest automation recognizing the subwords of a text.", Theoretical Computer Science, 40: 31–55, doi:10.1016/0304-3975(85)90157-4
  2. Navarro, Gonzalo (2001), "A guided tour to approximate string matching" (PDF), ACM Computing Surveys, 33 (1): 31–88, CiteSeerX 10.1.1.452.6317, doi:10.1145/375360.375365
  3. Crochemore, Maxime; Rytter, Wojciech (2003), Jewels of stringology: text algorithms

Further reading
  • Inenaga, S.; Hoshino, H.; Shinohara, A.; Takeda, M.; Arikawa, S. (2001), "On-line construction of symmetric compact directed acyclic word graphs", Proc. 8th Int. Symp. String Processing and Information Retrieval, 2001. SPIRE 2001, pp. 96–110, CiteSeerX 10.1.1.799.9933, doi:10.1109/SPIRE.2001.989743, ISBN 978-0-7695-1192-4.
  • Crochemore, Maxime; Vérin, Renaud (1997), "Direct construction of compact directed acyclic word graphs", Combinatorial Pattern Matching, Lecture Notes in Computer Science, 1264, Springer-Verlag, pp. 116–129, CiteSeerX 10.1.1.53.6273, doi:10.1007/3-540-63220-4_55, ISBN 978-3-540-63220-7.
  • Epifanio, Chiara; Mignosi, Filippo; Shallit, Jeffrey; Venturini, Ilaria (2004), "Sturmian graphs and a conjecture of Moser", in Calude, Cristian S.; Calude, Elena; Dineen, Michael J. (eds.), Developments in language theory. Proceedings, 8th international conference (DLT 2004), Auckland, New Zealand, December 2004, Lecture Notes in Computer Science, 3340, Springer-Verlag, pp. 175–187, ISBN 978-3-540-24014-3, Zbl 1117.68454
  • Do, H.H.; Sung, W.K. (2011), "Compressed Directed Acyclic Word Graph with Application in Local Alignment", Computing and Combinatorics, Lecture Notes in Computer Science, 6842, Springer-Verlag, pp. 503–518, doi:10.1007/978-3-642-22685-4_44, ISBN 978-3-642-22684-7
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.