Apéry's constant
In mathematics, at the intersection of number theory and special functions, Apéry's constant is the sum of the inverses of the positive cubes. That is, it is defined as the number
| Binary | 1.0011001110111010… |
| Decimal | 1.2020569031595942854… |
| Hexadecimal | 1.33BA004F00621383… |
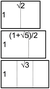
| Continued fraction | Note that this continued fraction is infinite, but it is not known whether this continued fraction is periodic or not. |
where ζ is the Riemann zeta function. It has an approximate value of[1]
The constant is named after Roger Apéry. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics. It also arises in the analysis of random minimum spanning trees[2] and in conjunction with the gamma function when solving certain integrals involving exponential functions in a quotient which appear occasionally in physics, for instance when evaluating the two-dimensional case of the Debye model and the Stefan–Boltzmann law.
Irrational number
ζ(3) was named Apéry's constant after the French mathematician Roger Apéry, who proved in 1978 that it is an irrational number.[3] This result is known as Apéry's theorem. The original proof is complex and hard to grasp,[4] and simpler proofs were found later.[5][6]
Beuker's simplified irrationality proof involves approximating the integrand of the known triple integral for ,
by the Legendre polynomials. In particular, van der Poorten's article chronicles this approach by noting that
where , are the Legendre polynomials, and the subsequences are integers or almost integers.
It is still not known whether Apéry's constant is transcendental.
Series representations
Classical
In addition to the fundamental series:
Leonhard Euler gave the series representation:[7]
in 1772, which was subsequently rediscovered several times.[8]
Other classical series representations include:
Fast convergence
Since the 19th century, a number of mathematicians have found convergence acceleration series for calculating decimal places of ζ(3). Since the 1990s, this search has focused on computationally efficient series with fast convergence rates (see section "Known digits").
The following series representation was found by A.A. Markov in 1890[9], rediscovered by Hjortnaes in 1953,[10] and rediscovered once more and widely advertised by Apéry in 1979:[3]
The following series representation, found by Amdeberhan in 1996,[11] gives (asymptotically) 1.43 new correct decimal places per term:
The following series representation, found by Amdeberhan and Zeilberger in 1997,[12] gives (asymptotically) 3.01 new correct decimal places per term:
The following series representation, found by Sebastian Wedeniwski in 1998,[13] gives (asymptotically) 5.04 new correct decimal places per term:
It was used by Wedeniwski to calculate Apéry's constant with several million correct decimal places.[14]
The following series representation, found by Mohamud Mohammed in 2005,[15] gives (asymptotically) 3.92 new correct decimal places per term:
Digit by digit
In 1998, Broadhurst[16] gave a series representation that allows arbitrary binary digits to be computed, and thus, for the constant to be obtained in nearly linear time, and logarithmic space.
Others
The following series representation was found by Ramanujan:[17]
The following series representation was found by Simon Plouffe in 1998:[18]
Srivastava[19] collected many series that converge to Apéry's constant.
Integral representations
There are numerous integral representations for Apéry's constant. Some of them are simple, others are more complicated.
Simple formulas
For example, this one follows from the summation representation for Apéry's constant:
- .
The next two follow directly from the well-known integral formulas for the Riemann zeta function:
and
- .
This one follows from a Taylor expansion of χ3(eix) about x = ±π/2, where χν(z) is the Legendre chi function:
Note the similarity to
where G is Catalan's constant.
More complicated formulas
For example, one formula was found by Johan Jensen:[20]
- ,
another by F. Beukers:[5]
- ,
Mixing these two formula, one can obtain :
- ,
By symmetry,
- ,
Summing both, .
Yet another by Iaroslav Blagouchine:[21]
- .
Evgrafov et al.'s connection to the derivatives of the gamma function
is also very useful for the derivation of various integral representations via the known integral formulas for the gamma and polygamma-functions.[22]
Known digits
The number of known digits of Apéry's constant ζ(3) has increased dramatically during the last decades. This is due both to the increasing performance of computers and to algorithmic improvements.
| Date | Decimal digits | Computation performed by |
|---|---|---|
| 1735 | 16 | Leonhard Euler |
| unknown | 16 | Adrien-Marie Legendre |
| 1887 | 32 | Thomas Joannes Stieltjes |
| 1996 | 520000 | Greg J. Fee & Simon Plouffe |
| 1997 | 1000000 | Bruno Haible & Thomas Papanikolaou |
| May 1997 | 10536006 | Patrick Demichel |
| February 1998 | 14000074 | Sebastian Wedeniwski |
| March 1998 | 32000213 | Sebastian Wedeniwski |
| July 1998 | 64000091 | Sebastian Wedeniwski |
| December 1998 | 128000026 | Sebastian Wedeniwski[1] |
| September 2001 | 200001000 | Shigeru Kondo & Xavier Gourdon |
| February 2002 | 600001000 | Shigeru Kondo & Xavier Gourdon |
| February 2003 | 1000000000 | Patrick Demichel & Xavier Gourdon[23] |
| April 2006 | 10000000000 | Shigeru Kondo & Steve Pagliarulo |
| January 2009 | 15510000000 | Alexander J. Yee & Raymond Chan[24] |
| March 2009 | 31026000000 | Alexander J. Yee & Raymond Chan[24] |
| September 2010 | 100000001000 | Alexander J. Yee[25] |
| September 2013 | 200000001000 | Robert J. Setti[25] |
| August 2015 | 250000000000 | Ron Watkins[25] |
| November 2015 | 400000000000 | Dipanjan Nag[26] |
| August 2017 | 500000000000 | Ron Watkins[25] |
| June 2019 | 1000000000000 | Ian Cutress[27] |
Reciprocal
The reciprocal of ζ(3) is the probability that any three positive integers, chosen at random, will be relatively prime (in the sense that as N goes to infinity, the probability that three positive integers less than N chosen uniformly at random will be relatively prime approaches this value).[28]
Extension to ζ(2n + 1)
Many people have tried to extend Apéry's proof that ζ(3) is irrational to other values of the zeta function with odd arguments. In 2000, Tanguy Rivoal showed that infinitely many of the numbers ζ(2n + 1) must be irrational.[29] In 2001, Wadim Zudilin proved that at least one of the numbers ζ(5), ζ(7), ζ(9), and ζ(11) must be irrational.[30]
See also
Notes
- See Wedeniwski 2001.
- See Frieze 1985.
- See Apéry 1979.
- See van der Poorten 1979.
- See Beukers 1979.
- See Zudilin 2002.
- See Euler 1773.
- See Srivastava 2000, p. 571 (1.11).
- See Markov 1890.
- See Hjortnaes 1953.
- See Amdeberhan 1996.
- See Amdeberhan & Zeilberger 1997.
- See Wedeniwski 1998 and Wedeniwski 2001. In his message to Simon Plouffe, Sebastian Wedeniwski states that he derived this formula from Amdeberhan & Zeilberger 1997. The discovery year (1998) is mentioned in Simon Plouffe's Table of Records (8 April 2001).
- See Wedeniwski 1998 and Wedeniwski 2001.
- See Mohammed 2005.
- See Broadhurst 1998.
- See Berndt 1989, chapter 14, formulas 25.1 and 25.3.
- See Plouffe 1998.
- See Srivastava 2000.
- See Jensen 1895.
- See Blagouchine 2014.
- See Evgrafov et al. 1969, exercise 30.10.1.
- See Gourdon & Sebah 2003.
- See Yee 2009.
- See Yee 2017.
- See Nag 2015.
- "Records set by y-cruncher". Retrieved June 8, 2019.
- Mollin (2009).
- See Rivoal 2000.
- See Zudilin 2001.
References
- Amdeberhan, Tewodros (1996), "Faster and faster convergent series for ", El. J. Combinat., 3 (1).
- Amdeberhan, Tewodros; Zeilberger, Doron (1997), "Hypergeometric Series Acceleration Via the WZ method", El. J. Combinat., 4 (2).
- Apéry, Roger (1979), "Irrationalité de et ", Astérisque, 61: 11–13.
- Berndt, Bruce C. (1989), Ramanujan's notebooks, Part II, Springer.
- Beukers, F. (1979), "A Note on the Irrationality of and ", Bull. London Math. Soc., 11 (3): 268–272, doi:10.1112/blms/11.3.268.
- Blagouchine, Iaroslav V. (2014), "Rediscovery of Malmsten's integrals, their evaluation by contour integration methods and some related results", The Ramanujan Journal, 35 (1): 21–110, doi:10.1007/s11139-013-9528-5.
- Broadhurst, D.J. (1998), Polylogarithmic ladders, hypergeometric series and the ten millionth digits of and , arXiv:math.CA/9803067.
- Euler, Leonhard (1773), "Exercitationes analyticae" (PDF), Novi Commentarii Academiae Scientiarum Petropolitanae (in Latin), 17: 173–204, retrieved 2008-05-18.
- Evgrafov, M. A.; Bezhanov, K. A.; Sidorov, Y. V.; Fedoriuk, M. V.; Shabunin, M. I. (1969), A Collection of Problems in the Theory of Analytic Functions [in Russian], Moscow: Nauka.
- Frieze, A. M. (1985), "On the value of a random minimum spanning tree problem", Discrete Applied Mathematics, 10 (1): 47–56, doi:10.1016/0166-218X(85)90058-7, MR 0770868.
- Gourdon, Xavier; Sebah, Pascal (2003), The Apéry's constant: .
- Hjortnaes, M. M. (August 1953), Overføring av rekken til et bestemt integral, in Proc. 12th Scandinavian Mathematical Congress, Lund, Sweden: Scandinavian Mathematical Society, pp. 211–213.
- Jensen, Johan Ludwig William Valdemar (1895), "Note numéro 245. Deuxième réponse. Remarques relatives aux réponses du MM. Franel et Kluyver", L'Intermédiaire des Mathématiciens, II: 346–347.
- Markov, A.A. (1890), "Mémoire sur la transformation des séries peu convergentes en séries très convergentes", Mém. de l’Acad. Imp. Sci. de St. Pétersbourg, t. XXXVII, No. 9: 18pp.
- Mohammed, Mohamud (2005), "Infinite families of accelerated series for some classical constants by the Markov-WZ method", Discrete Mathematics and Theoretical Computer Science, 7: 11–24.
- Mollin, Richard A. (2009), Advanced Number Theory with Applications, Discrete Mathematics and Its Applications, CRC Press, p. 220, ISBN 9781420083293.
- Plouffe, Simon (1998), Identities inspired from Ramanujan Notebooks II.
- Plouffe, Simon, Zeta(3) or Apéry constant to 2000 places.
- Ramaswami, V. (1934), "Notes on Riemann's -function", J. London Math. Soc., 9 (3): 165–169, doi:10.1112/jlms/s1-9.3.165.
- Rivoal, Tanguy (2000), "La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs", Comptes Rendus de l'Académie des Sciences, Série I, 331 (4): 267–270, arXiv:math/0008051, Bibcode:2000CRASM.331..267R, doi:10.1016/S0764-4442(00)01624-4.
- Setti, Robert J. (2015), Apéry's Constant - Zeta(3) - 200 Billion Digits, archived from the original on 2013-10-08.
- Srivastava, H. M. (December 2000), "Some Families of Rapidly Convergent Series Representations for the Zeta Functions" (PDF), Taiwanese Journal of Mathematics, 4 (4): 569–599, OCLC 36978119, retrieved 2015-08-22.
- van der Poorten, Alfred (1979), "A proof that Euler missed ... Apéry's proof of the irrationality of " (PDF), The Mathematical Intelligencer, 1 (4): 195–203, doi:10.1007/BF03028234, archived from the original (PDF) on 2011-07-06.
- Wedeniwski, Sebastian (2001), Simon Plouffe (ed.), The Value of Zeta(3) to 1,000,000 places, Project Gutenberg (Message to Simon Plouffe, with all decimal places but a shorter text edited by Simon Plouffe).
- Wedeniwski, Sebastian (13 December 1998), The Value of Zeta(3) to 1,000,000 places (Message to Simon Plouffe, with original text but only some decimal places).
- Weisstein, Eric W. "Apéry's constant". MathWorld.
- Yee, Alexander J. (2009), Large Computations.
- Yee, Alexander J. (2017), Zeta(3) - Apéry's Constant
- Nag, Dipanjan (2015), Calculated Apéry's constant to 400,000,000,000 Digit, A world record
- Zudilin, Wadim (2001), "One of the numbers , , , is irrational", Russ. Math. Surv., 56 (4): 774–776, Bibcode:2001RuMaS..56..774Z, doi:10.1070/RM2001v056n04ABEH000427.
- Zudilin, Wadim (2002), An elementary proof of Apéry's theorem, arXiv:math/0202159, Bibcode:2002math......2159Z.
Credits
This article incorporates material from Apéry's constant on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.