Activation function
In artificial neural networks, the activation function of a node defines the output of that node given an input or set of inputs. A standard integrated circuit can be seen as a digital network of activation functions that can be "ON" (1) or "OFF" (0), depending on input. This is similar to the behavior of the linear perceptron in neural networks. However, only nonlinear activation functions allow such networks to compute nontrivial problems using only a small number of nodes.[1]
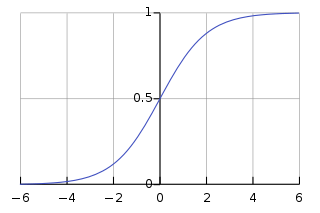
Functions
In biologically inspired neural networks, the activation function is usually an abstraction representing the rate of action potential firing in the cell.[2] In its simplest form, this function is binary—that is, either the neuron is firing or not. The function looks like , where is the Heaviside step function.
A line of positive slope may be used to reflect the increase in firing rate that occurs as input current increases. Such a function would be of the form , where is the slope. This activation function is linear and therefore cannot make decisions.
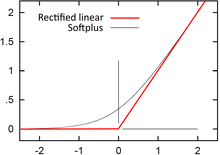
As biological neurons cannot lower their firing rate below zero, rectified linear activation functions are used: . They introduce a non-linearity at zero that can be used for decision making.[3]
Neurons also cannot fire faster than a certain rate. Sigmoid activation functions use a second non-linearity for large inputs: . Because they are in the range between zero and one, sigmoid activations can be interpreted as probabilities. If a range from -1 to 1 is desired, the sigmoid can be scaled and shifted to yield the hyperbolic tangent activation function: .
Alternative structures
A special class of activation functions known as radial basis functions (RBFs) are used in RBF networks, which are extremely efficient as universal function approximators. These activation functions can take many forms, but they are usually found as one of three functions:
- Gaussian:
- Multiquadratics:
- Inverse multiquadratics:
where is the vector representing the function center and and are parameters affecting the spread of the radius.
A computationally efficient Radial Basis Function has been proposed,[4] called Square-law based RBF kernel (SQ-RBF) which eliminates the exponential term as found in Gaussian RBF.
- SQ-RBF:
Support-vector machines (SVMs) can effectively utilize a class of activation functions that includes both sigmoids and RBFs. In this case, the input is transformed to reflect a decision boundary hyperplane based on a few training inputs called support-vectors . The activation function for the hidden layer of these machines is referred to as the inner product kernel, . The support-vectors are represented as the centers in RBFs with the kernel equal to the activation function, but they take a unique form in the perceptron as
- ,
where and must satisfy certain conditions for convergence. These machines can also accept arbitrary-order polynomial activation functions where
- .[5]
Activation function having types:
- Identity function
- Binary step function
- Bipolar step function
- Sigmoidal function
- Binary sigmoidal function
- Bipolar sigmoidal function
- Ramp function
Comparison of activation functions
Some desirable properties in an activation function include:
- Nonlinear – When the activation function is non-linear, then a two-layer neural network can be proven to be a universal function approximator.[6] This is known as the Universal Approximation Theorem. The identity activation function does not satisfy this property. When multiple layers use the identity activation function, the entire network is equivalent to a single-layer model.
- Range – When the range of the activation function is finite, gradient-based training methods tend to be more stable, because pattern presentations significantly affect only limited weights. When the range is infinite, training is generally more efficient because pattern presentations significantly affect most of the weights. In the latter case, smaller learning rates are typically necessary.
- Continuously differentiable – This property is desirable (RELU is not continuously differentiable and has some issues with gradient-based optimization, but it is still possible) for enabling gradient-based optimization methods. The binary step activation function is not differentiable at 0, and it differentiates to 0 for all other values, so gradient-based methods can make no progress with it.[7]
- Monotonic – When the activation function is monotonic, the error surface associated with a single-layer model is guaranteed to be convex.[8]
- Smooth functions with a monotonic derivative – These have been shown to generalize better in some cases.
- Approximates identity near the origin – When activation functions have this property, the neural network will learn efficiently when its weights are initialized with small random values. When the activation function does not approximate identity near the origin, special care must be used when initializing the weights.[9] In the table below, activation functions where and and is continuous at 0 are indicated as having this property.
The following table compares the properties of several activation functions that are functions of one fold x from the previous layer or layers:
| Name | Plot | Equation | Derivative (with respect to x) | Range | Order of continuity | Monotonic | Monotonic derivative | Approximates identity near the origin |
|---|---|---|---|---|---|---|---|---|
| Identity |  |
Yes | Yes | Yes | ||||
| Binary step |  |
Yes | No | No | ||||
| Logistic (a.k.a. Sigmoid or Soft step) | 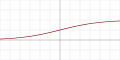 |
Yes | No | No | ||||
| TanH | 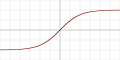 |
Yes | No | Yes | ||||
| SQNL[10] |  |
Yes | No | Yes | ||||
| ArcTan | 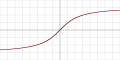 |
Yes | No | Yes | ||||
| ArSinH | Yes | No | Yes | |||||
| ElliotSig[11][12] Softsign[13][14] | 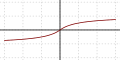 |
Yes | No | Yes | ||||
| Inverse square root unit (ISRU)[15] |  |
Yes | No | Yes | ||||
| Inverse square root linear unit (ISRLU)[15] | 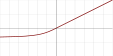 |
Yes | Yes | Yes | ||||
| Piecewise Linear Unit (PLU)[16] | 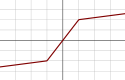 |
Yes | No | Yes | ||||
| Rectified linear unit (ReLU)[17] | 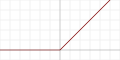 |
Yes | Yes | No | ||||
| Bipolar rectified linear unit (BReLU)[18] | .png) |
Yes | Yes | No | ||||
| Leaky rectified linear unit (Leaky ReLU)[19] | 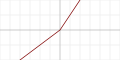 |
Yes | Yes | No | ||||
| Parameteric rectified linear unit (PReLU)[20] |  |
Yes iff | Yes | Yes iff | ||||
| Randomized leaky rectified linear unit (RReLU)[21] |  |
Yes | Yes | No | ||||
| Gaussian Error Linear Unit (GELU)[22] | 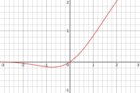 |
No | No | No | ||||
| Exponential linear unit (ELU)[23] | 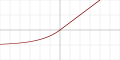 |
Yes iff | Yes iff | Yes iff | ||||
| Scaled exponential linear unit (SELU)[24] |
with and |
Yes | No | No | ||||
| S-shaped rectified linear activation unit (SReLU)[25] | are parameters. |
No | No | No | ||||
| Adaptive piecewise linear (APL)[26] | No | No | No | |||||
| SoftPlus[27] | 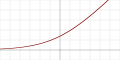 |
Yes | Yes | No | ||||
| Bent identity | 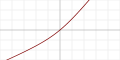 |
Yes | Yes | Yes | ||||
| Sigmoid Linear Unit (SiLU)[22] (AKA SiL[28] and Swish-1[29]) | 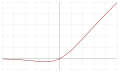 |
No | No | Approximates identity/2 | ||||
| SoftExponential[30] |  |
Yes | Yes | Yes iff | ||||
| Soft Clipping [31][32] | 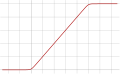 |
Yes | No | No | ||||
| Squashing[32][33][34] | 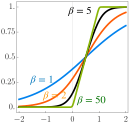 |
Yes | No | No | ||||
| Sinusoid[35] | 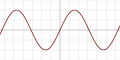 |
No | No | Yes | ||||
| Sinc | 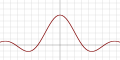 |
No | No | No | ||||
| Gaussian | 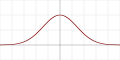 |
No | No | No | ||||
| SQ-RBF | No | No | No |
- ^ Here, H is the Heaviside step function.
- ^ α is a stochastic variable sampled from a uniform distribution at training time and fixed to the expectation value of the distribution at test time.
- ^ ^ ^ Here, is the logistic function.
- ^ for the range to hold true.
The following table lists activation functions that are not functions of a single fold x from the previous layer or layers:
| Name | Equation | Derivatives | Range | Order of continuity |
|---|---|---|---|---|
| Softmax | for i = 1, …, J | |||
| Maxout[36] |
^ Here, is the Kronecker delta.
See also
References
- Hinkelmann, Knut. "Neural Networks, p. 7" (PDF). University of Applied Sciences Northwestern Switzerland.
- Hodgkin, A. L.; Huxley, A. F. (1952-08-28). "A quantitative description of membrane current and its application to conduction and excitation in nerve". The Journal of Physiology. 117 (4): 500–544. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237.
- Behnke, Sven (2003). Hierarchical Neural Networks for Image Interpretation. Lecture Notes in Computer Science. 2766. Springer. doi:10.1007/b11963. ISBN 978-3-540-40722-5.
- Wuraola, Adedamola; Patel, Nitish (2018), "Computationally Efficient Radial Basis Function", 2018 International Conference on Neural Information Processing (ICONIP), Siem reap Cambodia: Springer, pp. 103–112, doi:10.1007/978-3-030-04179-3_9
- Haykin, Simon S. (1999). Neural Networks: A Comprehensive Foundation. Prentice Hall. ISBN 978-0-13-273350-2.
- Cybenko, G. (December 1989). "Approximation by superpositions of a sigmoidal function". Mathematics of Control, Signals, and Systems. 2 (4): 303–314. doi:10.1007/BF02551274. ISSN 0932-4194.
- Snyman, Jan (3 March 2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Science & Business Media. ISBN 978-0-387-24348-1.
- Wu, Huaiqin (2009). "Global stability analysis of a general class of discontinuous neural networks with linear growth activation functions". Information Sciences. 179 (19): 3432–3441. doi:10.1016/j.ins.2009.06.006.
- Sussillo, David; Abbott, L. F. (2014-12-19). "Random Walk Initialization for Training Very Deep Feedforward Networks". arXiv:1412.6558 [cs.NE].
- Wuraola, Adedamola; Patel, Nitish (2018), "SQNL:A New Computationally Efficient Activation Function", 2018 International Joint Conference on Neural Networks (IJCNN), Rio Rio de Janeiro, Brazil: IEEE, pp. 1–7
- Elliot, David L. (1993), "A better activation function for artificial neural networks", ISR Technical Report TR 93-8, University of Maryland, College Park, MD 20742., CiteSeerX 10.1.1.46.7204
- "elliotsig, Elliot symmetric sigmoid transfer function", command introduced in Matlab R2012b, Matlab Documentation, MathWorks.
- Bergstra, James; Desjardins, Guillaume; Lamblin, Pascal; Bengio, Yoshua (2009). "Quadratic polynomials learn better image features". Technical Report 1337". Département d’Informatique et de Recherche Opérationnelle, Université de Montréal. Archived from the original on 2018-09-25.
- Glorot, Xavier; Bengio, Yoshua (2010), "Understanding the difficulty of training deep feedforward neural networks" (PDF), International Conference on Artificial Intelligence and Statistics (AISTATS'10), Society for Artificial Intelligence and Statistics
- Carlile, Brad; Delamarter, Guy; Kinney, Paul; Marti, Akiko; Whitney, Brian (2017-11-09). "Improving Deep Learning by Inverse Square Root Linear Units (ISRLUs)". arXiv:1710.09967 [cs.LG].
- Nicolae, Andrei (2018-09-03). "PLU: The Piecewise Linear Unit Activation Function". arXiv:1809.09534 [cs.NE].
- Nair, Vinod; Hinton, Geoffrey E. (2010), "Rectified Linear Units Improve Restricted Boltzmann Machines", 27th International Conference on International Conference on Machine Learning, ICML'10, USA: Omnipress, pp. 807–814, ISBN 9781605589077
- Eidnes, Lars; Nøkland, Arild (2018). "Shifting Mean Activation Towards Zero with Bipolar Activation Functions". International Conference on Learning Representations (ICLR) Workshop. arXiv:1709.04054. Bibcode:2017arXiv170904054E.
- Maas, Andrew L.; Hannun, Awni Y.; Ng, Andrew Y. (June 2013). "Rectifier nonlinearities improve neural network acoustic models". Proc. ICML. 30 (1). S2CID 16489696.
- He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015-02-06). "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification". arXiv:1502.01852 [cs.CV].
- Xu, Bing; Wang, Naiyan; Chen, Tianqi; Li, Mu (2015-05-04). "Empirical Evaluation of Rectified Activations in Convolutional Network". arXiv:1505.00853 [cs.LG].
- Hendrycks, Dan; Gimpel, Kevin (2016). "Gaussian Error Linear Units (GELUs)". arXiv:1606.08415 [cs.LG].
- Clevert, Djork-Arné; Unterthiner, Thomas; Hochreiter, Sepp (2015-11-23). "Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)". arXiv:1511.07289 [cs.LG].
- Klambauer, Günter; Unterthiner, Thomas; Mayr, Andreas; Hochreiter, Sepp (2017-06-08). "Self-Normalizing Neural Networks". Advances in Neural Information Processing Systems. 30 (2017). arXiv:1706.02515. Bibcode:2017arXiv170602515K.
- Jin, Xiaojie; Xu, Chunyan; Feng, Jiashi; Wei, Yunchao; Xiong, Junjun; Yan, Shuicheng (2015-12-22). "Deep Learning with S-shaped Rectified Linear Activation Units". arXiv:1512.07030 [cs.CV].
- Forest Agostinelli; Matthew Hoffman; Peter Sadowski; Pierre Baldi (21 Dec 2014). "Learning Activation Functions to Improve Deep Neural Networks". arXiv:1412.6830 [cs.NE].
- Glorot, Xavier; Bordes, Antoine; Bengio, Yoshua (2011). "Deep sparse rectifier neural networks" (PDF). International Conference on Artificial Intelligence and Statistics.
- Elfwing, Stefan; Uchibe, Eiji; Doya, Kenji (2018). "Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning". Neural Networks. 107: 3–11. arXiv:1702.03118. doi:10.1016/j.neunet.2017.12.012. PMID 29395652.
- Ramachandran, Prajit; Zoph, Barret; Le, Quoc V (2017). "Searching for Activation Functions". arXiv:1710.05941 [cs.NE].
- Godfrey, Luke B.; Gashler, Michael S. (2016-02-03). "A continuum among logarithmic, linear, and exponential functions, and its potential to improve generalization in neural networks". 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management: KDIR. 1602: 481–486. arXiv:1602.01321. Bibcode:2016arXiv160201321G.
- Klimek, Matthew D.; Perelstein, Maxim (2018-10-26). "Neural Network-Based Approach to Phase Space Integration". arXiv:1810.11509 [hep-ph].
- Csiszár, Orsolya; Csiszár, Gábor; Dombi, József (2020-04-28). "Interpretable neural networks based on continuous-valued logic and multicriteria decision operators". Knowledge-Based Systems. 199: 105972. arXiv:1910.02486. doi:10.1016/j.knosys.2020.105972. ISSN 0950-7051.
- Urenda, Julio; Csiszár, Orsoly; Csiszár, Gábor; Dombi, József; Kosheleva, Olga; Kreinovich, Vladik; Eigner, György (2020-02-01). "Why Squashing Functions in Multi-Layer Neural Networks". Departmental Technical Reports (CS).
- Dombi, József; Gera, Zsolt (September 2005). "The approximation of piecewise linear membership functions and Łukasiewicz operators". Fuzzy Sets and Systems. 154 (2): 275–286. doi:10.1016/j.fss.2005.02.016.
- Gashler, Michael S.; Ashmore, Stephen C. (2014-05-09). "Training Deep Fourier Neural Networks To Fit Time-Series Data". arXiv:1405.2262 [cs.NE].
- Goodfellow, Ian J.; Warde-Farley, David; Mirza, Mehdi; Courville, Aaron; Bengio, Yoshua (2013). "Maxout Networks". JMLR Workshop and Conference Proceedings. 28 (3): 1319–1327. arXiv:1302.4389. Bibcode:2013arXiv1302.4389G.