Zernike polynomials

The first 21 Zernike polynomials, ordered vertically by radial degree and horizontally by azimuthal degree

In mathematics, the Zernike polynomials are a sequence of polynomials that are orthogonal on the unit disk. Named after optical physicist Frits Zernike, winner of the 1953 Nobel Prize in Physics and the inventor of phase-contrast microscopy, they play an important role in beam optics.^[1]^[2]

Definitions

There are even and odd Zernike polynomials. The even ones are defined as

Z_{n}^{{m}}(\rho ,\varphi )=R_{n}^{m}(\rho )\,\cos(m\,\varphi )\!

and the odd ones as

Z_{n}^{{-m}}(\rho ,\varphi )=R_{n}^{m}(\rho )\,\sin(m\,\varphi ),\!

where m and n are nonnegative integers with n ≥ m, φ is the azimuthal angle, ρ is the radial distance $0\leq \rho \leq 1$ , and R^m_n are the radial polynomials defined below. Zernike polynomials have the property of being limited to a range of −1 to +1, i.e. $|Z_{n}^{{m}}(\rho ,\varphi )|\leq 1$ . The radial polynomials R^m_n are defined as

R_{n}^{m}(\rho )=\sum _{{k=0}}^{{{\tfrac {n-m}{2}}}}{\frac {(-1)^{k}\,(n-k)!}{k!\left({\tfrac {n+m}{2}}-k\right)!\left({\tfrac {n-m}{2}}-k\right)!}}\;\rho ^{{n-2\,k}}

for n − m even, and are identically 0 for n − m odd.

Other representations

Rewriting the ratios of factorials in the radial part as products of binomials shows that the coefficients are integer numbers:

R_{n}^{m}(\rho )=\sum _{{k=0}}^{{{\tfrac {n-m}{2}}}}(-1)^{k}{\binom {n-k}{k}}{\binom {n-2k}{{\tfrac {n-m}{2}}-k}}\rho ^{{n-2k}}

.

A notation as terminating Gaussian hypergeometric functions is useful to reveal recurrences, to demonstrate that they are special cases of Jacobi polynomials, to write down the differential equations, etc.:

{\begin{aligned}R_{n}^{m}(\rho )&={\binom {n}{\tfrac {n+m}{2}}}\rho ^{n}\ {}_{2}F_{1}\left(-{\tfrac {n+m}{2}},-{\tfrac {n-m}{2}};-n;\rho ^{-2}\right)\\&=(-1)^{\tfrac {n-m}{2}}{\binom {\tfrac {n+m}{2}}{m}}\rho ^{m}\ {}_{2}F_{1}\left(1+{\tfrac {n+m}{2}},-{\tfrac {n-m}{2}};1+m;\rho ^{2}\right)\end{aligned}}

for n − m even.

The factor $\rho ^{n-2k}$ in the radial polynomial $R_{n}^{m}(\rho )$ may be expanded in a Bernstein basis of $b_{s,n/2}(\rho ^{2})$ for even $n$ or $\rho$ times a function of $b_{s,(n-1)/2}(\rho ^{2})$ for odd $n$ in the range $\lfloor n/2\rfloor -k\leq s\leq \lfloor n/2\rfloor$ . The radial polynomial may therefore be expressed by a finite number of Bernstein Polynomials with rational coefficients:

R_{n}^{m}(\rho )={\frac {1}{\binom {\lfloor n/2\rfloor }{\lfloor m/2\rfloor }}}\rho ^{n\mod 2}\sum _{s=\lfloor m/2\rfloor }^{\lfloor n/2\rfloor }(-1)^{\lfloor n/2\rfloor -s}{\binom {s}{\lfloor m/2\rfloor }}{\binom {(n+m)/2}{s+\lceil m/2\rceil }}b_{s,\lfloor n/2\rfloor }(\rho ^{2}).

Noll's sequential indices

Applications often involve linear algebra, where integrals over products of Zernike polynomials and some other factor build the matrix elements. To enumerate the rows and columns of these matrices by a single index, a conventional mapping of the two indices n and m to a single index j has been introduced by Noll.^[3] The table of this association $Z_{n}^{m}\rightarrow Z_{j}$ starts as follows (sequence A176988 in the OEIS). $j={\frac {n(n+1)}{2}}+|m|+\left\{{\begin{array}{ll}0,&m>0\land n\equiv \{0,1\}{\pmod {4}};\\0,&m<0\land n\equiv \{2,3\}{\pmod {4}};\\1,&m\geq 0\land n\equiv \{2,3\}{\pmod {4}};\\1,&m\leq 0\land n\equiv \{0,1\}{\pmod {4}}.\end{array}}\right.$

n,m	0,0	1,1	1,−1	2,0	2,−2	2,2	3,−1	3,1	3,−3	3,3
j	1	2	3	4	5	6	7	8	9	10
n,m	4,0	4,2	4,−2	4,4	4,−4	5,1	5,−1	5,3	5,−3	5,5
j	11	12	13	14	15	16	17	18	19	20

The rule is that the even Z (with even azimuthal part m, $\cos(m\varphi )$ ) obtain even indices j, the odd Z odd indices j. Within a given n, lower values of |m| obtain lower j.

OSA/ANSI standard indices

OSA ^[4] and ANSI single-index Zernike polynomials using:

j={\frac {n(n+2)+m}{2}}

n,m	0,0	1,-1	1,1	2,-2	2,0	2,2	3,-3	3,-1	3,1	3,3
j	0	1	2	3	4	5	6	7	8	9
n,m	4,-4	4,-2	4,0	4,2	4,4	5,-5	5,-3	5,-1	5,1	5,3
j	10	11	12	13	14	15	16	17	18	19

Fringe/Zemax indices

Zemax uses the Fringe indexing scheme.^[5]

$j=\left(1+{\frac {n+|m|}{2}}\right)^{2}-2|m|+{\frac {1-\operatorname {sgn} m}{2}}$

The first 20 fringe numbers are listed below.

n,m	0,0	1,1	1,−1	2,0	2,2	2,-2	3,1	3,-1	4,0	3,3
j	1	2	3	4	5	6	7	8	9	10
n,m	3,-3	4,2	4,−2	5,1	5,−1	6,0	4,4	4,-4	5,3	5,-3
j	11	12	13	14	15	16	17	18	19	20

Properties

Orthogonality

The orthogonality in the radial part reads^[6]

\int _{0}^{1}\rho {\sqrt {2n+2}}R_{n}^{m}(\rho )\,{\sqrt {2n'+2}}R_{{n'}}^{{m}}(\rho )\,d\rho =\delta _{{n,n'}}.

Orthogonality in the angular part is represented by the elementary

\int _{0}^{{2\pi }}\cos(m\varphi )\cos(m'\varphi )\,d\varphi =\epsilon _{m}\pi \delta _{{|m|,|m'|}},

\int _{0}^{{2\pi }}\sin(m\varphi )\sin(m'\varphi )\,d\varphi =(-1)^{{m+m'}}\pi \delta _{{|m|,|m'|}};\quad m\neq 0,

\int _{0}^{{2\pi }}\cos(m\varphi )\sin(m'\varphi )\,d\varphi =0,

where $\epsilon _{m}$ (sometimes called the Neumann factor because it frequently appears in conjunction with Bessel functions) is defined as 2 if $m=0$ and 1 if $m\neq 0$ . The product of the angular and radial parts establishes the orthogonality of the Zernike functions with respect to both indices if integrated over the unit disk,

\int Z_{n}^{m}(\rho ,\varphi )Z_{{n'}}^{{m'}}(\rho ,\varphi )\,d^{2}r={\frac {\epsilon _{m}\pi }{2n+2}}\delta _{{n,n'}}\delta _{{m,m'}},

where $d^{2}r=\rho \,d\rho \,d\varphi$ is the Jacobian of the circular coordinate system, and where $n-m$ and $n'-m'$ are both even.

A special value is

R_{n}^{m}(1)=1,\,

Zernike transform

Any sufficiently smooth real-valued phase field over the unit disk $G(\rho ,\varphi )$ can be represented in terms of its Zernike coefficients (odd and even), just as periodic functions find an orthogonal representation with the Fourier series. We have

G(\rho ,\varphi )=\sum _{{m,n}}\left[a_{{m,n}}Z_{n}^{{m}}(\rho ,\varphi )+b_{{m,n}}Z_{n}^{{-m}}(\rho ,\varphi )\right],

where the coefficients can be calculated using inner products. On the space of $L^{2}$ functions on the unit disk, there is an inner product defined by

\langle F,G\rangle :=\int F(\rho ,\varphi )G(\rho ,\varphi )\rho d\rho d\varphi .

The Zernike coefficients can then be expressed as follows:

{\begin{aligned}a_{{m,n}}&={\frac {2n+2}{\epsilon _{m}\pi }}\left\langle G(\rho ,\varphi ),Z_{n}^{{m}}(\rho ,\varphi )\right\rangle ,\\b_{{m,n}}&={\frac {2n+2}{\epsilon _{m}\pi }}\left\langle G(\rho ,\varphi ),Z_{n}^{{-m}}(\rho ,\varphi )\right\rangle .\end{aligned}}

Alternatively, one can use the known values of phase function G on the circular grid to form a system of equations. The phase function is retrieved by the unknown-coefficient weighted product with (known values) of Zernike polynomial across the unit grid. Hence, coefficients can also be found by solving a linear system, for instance by matrix inversion. Fast algorithms to calculate the forward and inverse Zernike transform use symmetry properties of trigonometric functions, separability of radial and azimuthal parts of Zernike polynomials, and their rotational symmetries.

Symmetries

The parity with respect to reflection along the x axis is

Z_{n}^{{m}}(\rho ,\varphi )=(-1)^{m}Z_{n}^{{m}}(\rho ,-\varphi ).

The parity with respect to point reflection at the center of coordinates is

Z_{n}^{m}(\rho ,\varphi )=(-1)^{m}Z_{n}^{m}(\rho ,\varphi +\pi ),

where $(-1)^{m}$ could as well be written $(-1)^{n}$ because $n-m$ is even for the relevant, non-vanishing values. The radial polynomials are also either even or odd, depending on order n or m:

R_{n}^{m}(\rho )=(-1)^{n}R_{n}^{m}(-\rho )=(-1)^{m}R_{n}^{m}(-\rho ).

The periodicity of the trigonometric functions implies invariance if rotated by multiples of $2\pi /m$ radian around the center:

Z_{n}^{m}\left(\rho ,\varphi +{\tfrac {2\pi k}{m}}\right)=Z_{n}^{m}(\rho ,\varphi ),\qquad k=0,\pm 1,\pm 2,\cdots .

Recurrence relations

The Zernike polynomials satisfy the following recurrence relation which depends neither on the degree nor on the azimuthal order of the radial polynomials:^[7]

{\begin{aligned}R_{n}^{m}(\rho )+R_{n-2}^{m}(\rho )=\rho \left[R_{n-1}^{\left|m-1\right|}(\rho )+R_{n-1}^{m+1}(\rho )\right]{\text{ .}}\end{aligned}}

From the definition of $R_{n}^{m}$ it can be seen that $R_{m}^{m}(\rho )=\rho ^{m}$ and $R_{m+2}^{m}(\rho )=((m+2)\rho ^{2}-(m+1))\rho ^{m}$ . The following three-term recurrence relation^[8] then allows to calculate all other $R_{n}^{m}(\rho )$ :

R_{n}^{m}(\rho )={\frac {2(n-1)(2n(n-2)\rho ^{2}-m^{2}-n(n-2))R_{n-2}^{m}(\rho )-n(n+m-2)(n-m-2)R_{n-4}^{m}(\rho )}{(n+m)(n-m)(n-2)}}{\text{ .}}

The above relation is especially useful since the derivative of $R_{n}^{m}$ can be calculated from two radial Zernike polynomials of adjacent degree:^[8]

{\frac {\operatorname {d} }{\operatorname {d} \!\rho }}R_{n}^{m}(\rho )={\frac {(2nm(\rho ^{2}-1)+(n-m)(m+n(2\rho ^{2}-1)))R_{n}^{m}(\rho )-(n+m)(n-m)R_{n-2}^{m}(\rho )}{2n\rho (\rho ^{2}-1)}}{\text{ .}}

Examples

Radial polynomials

The first few radial polynomials are:

R_{0}^{0}(\rho )=1\,

R_{1}^{1}(\rho )=\rho \,

R_{2}^{0}(\rho )=2\rho ^{2}-1\,

R_{2}^{2}(\rho )=\rho ^{2}\,

R_{3}^{1}(\rho )=3\rho ^{3}-2\rho \,

R_{3}^{3}(\rho )=\rho ^{3}\,

R_{4}^{0}(\rho )=6\rho ^{4}-6\rho ^{2}+1\,

R_{4}^{2}(\rho )=4\rho ^{4}-3\rho ^{2}\,

R_{4}^{4}(\rho )=\rho ^{4}\,

R_{5}^{1}(\rho )=10\rho ^{5}-12\rho ^{3}+3\rho \,

R_{5}^{3}(\rho )=5\rho ^{5}-4\rho ^{3}\,

R_{5}^{5}(\rho )=\rho ^{5}\,

R_{6}^{0}(\rho )=20\rho ^{6}-30\rho ^{4}+12\rho ^{2}-1\,

R_{6}^{2}(\rho )=15\rho ^{6}-20\rho ^{4}+6\rho ^{2}\,

R_{6}^{4}(\rho )=6\rho ^{6}-5\rho ^{4}\,

R_{6}^{6}(\rho )=\rho ^{6}.\,

Zernike polynomials

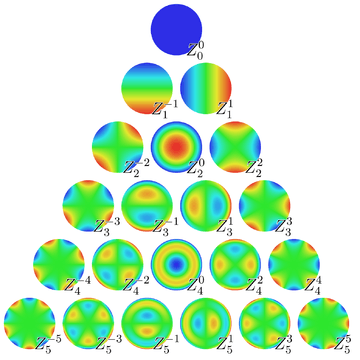
The first few Zernike modes, with OSA/ANSI and Noll single-indices, are shown below. They are normalized such that

\int _{0}^{{2\pi }}\int _{0}^{1}Z_{j}^{2}\,\rho \,d\rho \,d\theta =\pi .

	OSA/ANSI index ( $j$ )	Noll index ( $j$ )	Radial degree ( $n$ )	Azimuthal degree ( $m$ )	$Z_{j}$	Classical name
$Z_{0}^{0}$	00	01	0	00	$1$	Piston (see, Wigner semicircle distribution)
$Z_{1}^{-1}$	01	03	1	−1	$2\rho \sin \theta$	Tilt (Y-Tilt, vertical tilt)
$Z_{1}^{1}$	02	02	1	+1	$2\rho \cos \theta$	Tip (X-Tilt, horizontal tilt)
$Z_{2}^{-2}$	03	05	2	−2	${\sqrt {6}}\rho ^{2}\sin 2\theta$	Oblique astigmatism
$Z_{2}^{0}$	04	04	2	00	${\sqrt {3}}(2\rho ^{2}-1)$	Defocus (longitudinal position)
$Z_{2}^{2}$	05	06	2	+2	${\sqrt {6}}\rho ^{2}\cos 2\theta$	Vertical astigmatism
$Z_{3}^{-3}$	06	09	3	−3	${\sqrt {8}}\rho ^{3}\sin 3\theta$	Vertical trefoil
$Z_{3}^{-1}$	07	07	3	−1	${\sqrt {8}}(3\rho ^{3}-2\rho )\sin \theta$	Vertical coma
$Z_{3}^{1}$	08	08	3	+1	${\sqrt {8}}(3\rho ^{3}-2\rho )\cos \theta$	Horizontal coma
$Z_{3}^{3}$	09	10	3	+3	${\sqrt {8}}\rho ^{3}\cos 3\theta$	Oblique trefoil
$Z_{4}^{-4}$	10	15	4	−4	${\sqrt {10}}\rho ^{4}\sin 4\theta$	Oblique quadrafoil
$Z_{4}^{-2}$	11	13	4	−2	${\sqrt {10}}(4\rho ^{4}-3\rho ^{2})\sin 2\theta$	Oblique secondary astigmatism
$Z_{4}^{0}$	12	11	4	00	${\sqrt {5}}(6\rho ^{4}-6\rho ^{2}+1)$	Primary spherical
$Z_{4}^{2}$	13	12	4	+2	${\sqrt {10}}(4\rho ^{4}-3\rho ^{2})\cos 2\theta$	Vertical secondary astigmatism
$Z_{4}^{4}$	14	14	4	+4	${\sqrt {10}}\rho ^{4}\cos 4\theta$	Vertical quadrafoil

Applications

The functions are a basis defined over the circular support area, typically the pupil planes in classical optical imaging at visible and infrared wavelengths through systems of lenses and mirrors of finite diameter. Their advantages are the simple analytical properties inherited from the simplicity of the radial functions and the factorization in radial and azimuthal functions; this leads, for example, to closed-form expressions of the two-dimensional Fourier transform in terms of Bessel functions^[9]^[10]. Their disadvantage, in particular if high n are involved, is the unequal distribution of nodal lines over the unit disk, which introduces ringing effects near the perimeter $\rho \approx 1$ , which often leads attempts to define other orthogonal functions over the circular disk.^[11]^[12]^[13]

In precision optical manufacturing, Zernike polynomials are used to characterize higher-order errors observed in interferometric analyses. In optometry and ophthalmology, Zernike polynomials are used to describe aberrations of the cornea or lens from an ideal spherical shape, which result in refraction errors.

They are commonly used in adaptive optics, where they can be used to characterize atmospheric distortion. Obvious applications for this are IR or visual astronomy and satellite imagery.

Another application of the Zernike polynomials is found in the Extended Nijboer–Zernike theory of diffraction and aberrations.

Zernike polynomials are widely used as basis functions of image moments. Since Zernike polynomials are orthogonal to each other, Zernike moments can represent properties of an image with no redundancy or overlap of information between the moments. Although Zernike moments are significantly dependent on the scaling and the translation of the object in a region of interest (ROI), their magnitudes are independent of the rotation angle of the object.^[14] Thus, they can be utilized to extract features from images that describe the shape characteristics of an object. For instance, Zernike moments are utilized as shape descriptors to classify benign and malignant breast masses^[15] or the surface of vibrating disks^[16]. Zernike Moments also have been used to quantify shape of osteosarcoma cancer cell lines in single cell level.^[17]

Higher dimensions

The concept translates to higher dimensions D if multinomials $x_{1}^{i}x_{2}^{j}\cdots x_{D}^{k}$ in Cartesian coordinates are converted to hyperspherical coordinates, $\rho ^{s},s\leq D$ , multiplied by a product of Jacobi polynomials of the angular variables. In $D=3$ dimensions, the angular variables are spherical harmonics, for example. Linear combinations of the powers $\rho ^{s}$ define an orthogonal basis $R_{n}^{{(l)}}(\rho )$ satisfying

\int _{0}^{1}\rho ^{{D-1}}R_{n}^{{(l)}}(\rho )R_{{n'}}^{{(l)}}(\rho )d\rho =\delta _{{n,n'}}

.

(Note that a factor ${\sqrt {2n+D}}$ is absorbed in the definition of R here, whereas in $D=2$ the normalization is chosen slightly differently. This is largely a matter of taste, depending on whether one wishes to maintain an integer set of coefficients or prefers tighter formulas if the orthogonalization is involved.) The explicit representation is

{\begin{aligned}R_{n}^{{(l)}}(\rho )&={\sqrt {2n+D}}\sum _{{s=0}}^{{{\tfrac {n-l}{2}}}}(-1)^{s}{{\tfrac {n-l}{2}} \choose s}{n-s-1+{\tfrac {D}{2}} \choose {\tfrac {n-l}{2}}}\rho ^{{n-2s}}\\&=(-1)^{{{\tfrac {n-l}{2}}}}{\sqrt {2n+D}}\sum _{{s=0}}^{{{\tfrac {n-l}{2}}}}(-1)^{s}{{\tfrac {n-l}{2}} \choose s}{s-1+{\tfrac {n+l+D}{2}} \choose {\tfrac {n-l}{2}}}\rho ^{{2s+l}}\\&=(-1)^{{{\tfrac {n-l}{2}}}}{\sqrt {2n+D}}{{\tfrac {n+l+D}{2}}-1 \choose {\tfrac {n-l}{2}}}\rho ^{l}\ {}_{2}F_{1}\left(-{\tfrac {n-l}{2}},{\tfrac {n+l+D}{2}};l+{\tfrac {D}{2}};\rho ^{2}\right)\end{aligned}}

for even $n-l\geq 0$ , else identical to zero.

References

↑ Zernike, F. (1934). "Beugungstheorie des Schneidenverfahrens und Seiner Verbesserten Form, der Phasenkontrastmethode". Physica. 1 (8): 689–704. Bibcode:1934Phy.....1..689Z. doi:10.1016/S0031-8914(34)80259-5.
↑ Born, Max, and Wolf, Emil (1999). Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (7th ed.). Cambridge, UK: Cambridge University Press. p. 986. ISBN 9780521642224.
↑ Noll, R. J. (1976). "Zernike polynomials and atmospheric turbulence" (PDF). J. Opt. Soc. Am. 66 (3): 207. Bibcode:1976JOSA...66..207N. doi:10.1364/JOSA.66.000207.
↑ Thibos, L. N.; Applegate, R. A.; Schwiegerling, J. T.; Webb, R. (2002). "Standards for reporting the optical aberrations of eyes" (PDF). Journal of Refractive Surgery. 18 (5): S652–60.
↑ Genberg, V. L.; Michels, G. J.; Doyle, K. B. (2002). "Orthogonality of Zernike polynomials". Optomechanical design and Engineering 2002. Proc SPIE. 4771. pp. 276–286. doi:10.1117/12.482169.
↑ Lakshminarayanan, V.; Fleck, Andre (2011). "Zernike polynomials: a guide". J. Mod. Opt. 58 (7). pp. 545–561. Bibcode:2011JMOp...58..545L. doi:10.1080/09500340.2011.554896.
↑ Honarvar Shakibaei Asli, Barmak; Raveendran, Paramesran (July 2013). "Recursive formula to compute Zernike radial polynomials" Opt. Lett. (OSA) 38 (14): 2487–2489. doi:10.1364/OL.38.002487
1 2 Kintner, E. C. (1976). "On the mathematical properties of the Zernike Polynomials". Opt. Acta. 23 (8): 679–680. Bibcode:1976AcOpt..23..679K. doi:10.1080/713819334.
↑ Tatulli, E. (2013). "Transformation of Zernike coefficients: a Fourier-based method for scaled, translated, and rotated wavefront apertures". J. Opt. Soc. Am. A. 30 (4): 726–32. arXiv:1302.7106. Bibcode:2013JOSAA..30..726T. doi:10.1364/JOSAA.30.000726. PMID 23595334.
↑ Janssen, A. J. E. M. (2011). "New analytic results for the Zernike Circle Polynomials from a basic result in the Nijboer-Zernike diffraction theory". Journal of the European Optical Society: Rapid Publications. 6. doi:10.2971/jeos.2011.11028.
↑ Barakat, Richard (1980). "Optimum balanced wave-front aberrations for radially symmetric amplitude distributions: Generalizations of Zernike polynomials". J. Opt. Soc. Am. 70 (6): 739–742. Bibcode:1980JOSA...70..739B. doi:10.1364/JOSA.70.000739.
↑ Janssen, A. J. E. M. (2011). "A generalization of the Zernike circle polynomials for forward and inverse problems in diffraction theory". arXiv:1110.2369 [math-ph].
↑ Mathar, R. J. (2018). "Orthogonal basis function over the unit circle with the minimax property". arXiv:1802.09518 [math.NA].
↑ Tahmasbi, A. (2010). An Effective Breast Mass Diagnosis System using Zernike Moments. 17th Iranian Conf. on Biomedical Engineering (ICBME'2010). Isfahan, Iran: IEEE. pp. 1–4. doi:10.1109/ICBME.2010.5704941.
↑ Tahmasbi, A.; Saki, F.; Shokouhi, S.B. (2011). "Classification of Benign and Malignant Masses Based on Zernike Moments". Computers in Biology and Medicine. 41 (8): 726–735. doi:10.1016/j.compbiomed.2011.06.009. PMID 21722886.
↑ Rdzanek, W. P. (2018). "Sound radiation of a vibrating elastically supported circular plate embedded into a flat screen revisited using the Zernike circle polynomials". J. Sound Vibr. 434: 91–125. Bibcode:2018JSV...434...92R. doi:10.1016/j.jsv.2018.07.035.
↑ Alizadeh, Elaheh; Lyons, Samanthe M; Castle, Jordan M; Prasad, Ashok (2016). "Measuring systematic changes in invasive cancer cell shape using Zernike moments". Integrative Biology. 8 (11): 1183–1193. doi:10.1039/C6IB00100A. PMID 27735002.

Weisstein, Eric W. "Zernike Polynomial". MathWorld.
Andersen, Torben B. (2018). "Efficient and robust recurrence relations for the Zernike circle polynomials and their derivatives in Cartesian coordinates". Opt. Exp. 26 (15): 18878–18896. doi:10.1364/OE.26.018878. PMID 30114148.
Bhatia, A. B.; Wolf, E. (1952). "The Zernike circle polynomials occurring in diffraction theory". Proc. Phys. Soc. B. 65 (11): 909–910. Bibcode:1952PPSB...65..909B. doi:10.1088/0370-1301/65/11/112.
Callahan, P. G.; De Graef, M. (2012). "Precipitate shape fitting and reconstruction by means of 3D Zernike functions". Model. Simul. Mat. Sci. Engin. 20 (1): 015003. Bibcode:2012MSMSE..20a5003C. doi:10.1088/0965-0393/20/1/015003.
Campbell, C. E. (2003). "Matrix method to find a new set of Zernike coefficients form an original set when the aperture radius is changed". J. Opt. Soc. Am. A. 20 (2): 209. Bibcode:2003JOSAA..20..209C. doi:10.1364/JOSAA.20.000209.
Cerjan, C. (2007). "The Zernike-Bessel representation and its application to Hankel transforms". J. Opt. Soc. Am. A. 24 (6): 1609. Bibcode:2007JOSAA..24.1609C. doi:10.1364/JOSAA.24.001609.
Comastri, S. A.; Perez, L. I.; Perez, G. D.; Martin, G.; Bastida Cerjan, K. (2007). "Zernike expansion coefficients: rescaling and decentering for different pupils and evaluation of corneal aberrations". J. Opt. Soc. Am. A. 9 (3): 209–221. Bibcode:2007JOptA...9..209C. doi:10.1088/1464-4258/9/3/001.
Conforti, G. (1983). "Zernike aberration coefficients from Seidel and higher-order power-series coefficients". Opt. Lett. 8 (7): 407–408. Bibcode:1983OptL....8..407C. doi:10.1364/OL.8.000407.
Dai, G-m.; Mahajan, V. N. (2007). "Zernike annular polynomials and atmospheric turbulence". J. Opt. Soc. Am. A. 24 (1): 139. Bibcode:2007JOSAA..24..139D. doi:10.1364/JOSAA.24.000139.
Dai, G-m. (2006). "Scaling Zernike expansion coefficients to smaller pupil sizes: a simpler formula". J. Opt. Soc. Am. A. 23 (3): 539. Bibcode:2006JOSAA..23..539D. doi:10.1364/JOSAA.23.000539.
Díaz, J. A.; Fernández-Dorado, J.; Pizarro, C.; Arasa, J. (2009). "Zernike Coefficients for Concentric, Circular, Scaled Pupils: An Equivalent Expression". Journal of Modern Optics. 56 (1): 149–155. Bibcode:2009JMOp...56..149D. doi:10.1080/09500340802531224.
Díaz, J. A.; Fernández-Dorado, J. "Zernike Coefficients for Concentric, Circular, Scaled Pupils". from The Wolfram Demonstrations Project.
Farokhi, Sajad; Shamsuddin, Siti Mariyam; Flusser, Jan; Sheikh, U.U; Khansari, Mohammad; Jafari-Khouzani, Kourosh (2013). "Rotation and noise invariant near-infrared face recognition by means of Zernike moments and spectral regression discriminant analysis". Journal of Electronic Imaging. 22 (1): 013030. Bibcode:2013JEI....22a3030F. doi:10.1117/1.JEI.22.1.013030.
Gu, J.; Shu, H. Z.; Toumoulin, C.; Luo, L. M. (2002). "A novel algorithm for fast computation of Zernike moments". Pattern Recogn. 35 (12): 2905–2911. doi:10.1016/S0031-3203(01)00194-7.
Herrmann, J. (1981). "Cross coupling and aliasing in modal wave-front estimation". J. Opt. Soc. Am. 71 (8): 989. Bibcode:1981JOSA...71..989H. doi:10.1364/JOSA.71.000989.
Hu, P. H.; Stone, J.; Stanley, T. (1989). "Application of Zernike polynomials to atmospheric propagation problems". J. Opt. Soc. Am. A. 6 (10): 1595. Bibcode:1989JOSAA...6.1595H. doi:10.1364/JOSAA.6.001595.
Kintner, E. C. (1976). "On the mathematical properties of the Zernike Polynomials". Opt. Acta. 23 (8): 679–680. Bibcode:1976AcOpt..23..679K. doi:10.1080/713819334.
Lawrence, G. N.; Chow, W. W. (1984). "Wave-front tomography by Zernike Polynomial decomposition". Opt. Lett. 9 (7): 267. Bibcode:1984OptL....9..267L. doi:10.1364/OL.9.000267.
Liu, Haiguang; Morris, Richard J.; Hexemer, A.; Grandison, Scott; Zwart, Peter H. (2012). "Computation of small-angle scattering profiles with three-dimensional Zernike polynomials". Acta Crystallogr. A. 68 (2): 278–285. doi:10.1107/S010876731104788X. PMID 22338662.
Lundström, L.; Unsbo, P. (2007). "Transformation of Zernike coefficients: scaled, translated and rotated wavefronts with circular and elliptical pupils". J. Opt. Soc. Am. A. 24 (3): 569. Bibcode:2007JOSAA..24..569L. doi:10.1364/JOSAA.24.000569.
Mahajan, V. N. (1981). "Zernike annular polynomials for imaging systems with annular pupils". J. Opt. Soc. Am. 71: 75. Bibcode:1981JOSA...71...75M. doi:10.1364/JOSA.71.000075.
Mathar, R. J. (2007). "Third Order Newton's Method for Zernike Polynomial Zeros". arXiv:0705.1329 [math.NA].
Mathar, R. J. (2009). "Zernike Basis to Cartesian Transformations". Serbian Astronomical Journal. 179 (179): 107–120. arXiv:0809.2368. Bibcode:2009SerAJ.179..107M. doi:10.2298/SAJ0979107M.
Prata Jr, A.; Rusch, W. V. T. (1989). "Algorithm for computation of Zernike polynomials expansion coefficients". Appl. Opt. 28 (4): 749–54. Bibcode:1989ApOpt..28..749P. doi:10.1364/AO.28.000749. PMID 20548554.
Schwiegerling, J. (2002). "Scaling Zernike expansion coefficients to different pupil sizes". J. Opt. Soc. Am. A. 19 (10): 1937. Bibcode:2002JOSAA..19.1937S. doi:10.1364/JOSAA.19.001937.
Sheppard, C. J. R.; Campbell, S.; Hirschhorn, M. D. (2004). "Zernike expansion of separable functions in Cartesian coordinates". Appl. Opt. 43 (20): 3963. Bibcode:2004ApOpt..43.3963S. doi:10.1364/AO.43.003963.
Shu, H.; Luo, L.; Han, G.; Coatrieux, J.-L. (2006). "General method to derive the relationship between two sets of Zernike coefficients corresponding to different aperture sizes". J. Opt. Soc. Am. A. 23 (8): 1960. Bibcode:2006JOSAA..23.1960S. doi:10.1364/JOSAA.23.001960. PMC 1961626.
Swantner, W.; Chow, W. W. (1994). "Gram-Schmidt orthogonalization of Zernike polynomials for general aperture shapes". Appl. Opt. 33 (10): 1832–7. Bibcode:1994ApOpt..33.1832S. doi:10.1364/AO.33.001832. PMID 20885515.
Tango, W. J. (1977). "The circle polynomials of Zernike and their application in optics". Appl. Phys. A. 13 (4): 327–332. Bibcode:1977ApPhy..13..327T. doi:10.1007/BF00882606.
Tyson, R. K. (1982). "Conversion of Zernike aberration coefficients to Seidel and higher-order power series aberration coefficients". Opt. Lett. 7 (6): 262. Bibcode:1982OptL....7..262T. doi:10.1364/OL.7.000262.
Wang, J. Y.; Silva, D. E. (1980). "Wave-front interpretation with Zernike Polynomials". Appl. Opt. 19 (9): 1510–8. Bibcode:1980ApOpt..19.1510W. doi:10.1364/AO.19.001510. PMID 20221066.
Barakat, R. (1980). "Optimum balanced wave-front aberrations for radially symmetric amplitude distributions: Generalizations of Zernike polynomials". J. Opt. Soc. Am. 70 (6): 739. Bibcode:1980JOSA...70..739B. doi:10.1364/JOSA.70.000739.
ten Brummelaar, T. A. (1996). "Modeling atmospheric wave aberrations and astronomical instrumentation using the polynomials of Zernike". Opt. Commun. 132 (3–4): 329–342. Bibcode:1996OptCo.132..329T. doi:10.1016/0030-4018(96)00407-5.
Novotni, M.; Klein, R. (2003). 3D Zernike Descriptors for Content Based Shape Retrieval (PDF). Proceedings of the 8th ACM Symposium on Solid Modeling and Applications. p. 216. CiteSeerX 10.1.1.14.4970. doi:10.1145/781606.781639. ISBN 978-1581137064.
Novotni, M.; Klein, R. (2004). "Shape retrieval using 3D Zernike descriptors" (PDF). Computer Aided Design. 36 (11): 1047–1062. CiteSeerX 10.1.1.71.8238. doi:10.1016/j.cad.2004.01.005.
Farokhi, Sajad; Shamsuddin, Siti Mariyam; Sheikh, U.U; Flusser, Jan (2014). "Near Infrared Face Recognition: A Comparison of Moment-Based Approaches". Lecture Notes in Electrical Engineering. 291 (1): 129–135. doi:10.1007/978-981-4585-42-2_15.
Farokhi, Sajad; Shamsuddin, Siti Mariyam; Flusser, Jan; Sheikh, U.U; Khansari, Mohammad; Jafari-Khouzani, Kourosh (2014). "Near infrared face recognition by combining Zernike moments and undecimated discrete wavelet transform". Digital Signal Processing. 31 (1): 13–27. doi:10.1016/j.dsp.2014.04.008.

External links

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Zernike, F. (1934). "Beugungstheorie des Schneidenverfahrens und Seiner Verbesserten Form, der Phasenkontrastmethode". Physica. 1 (8): 689–704. Bibcode:1934Phy.....1..689Z. doi:10.1016/S0031-8914(34)80259-5.

[2] Born, Max, and Wolf, Emil (1999). Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (7th ed.). Cambridge, UK: Cambridge University Press. p. 986. ISBN 9780521642224.

[noll1976-3] Noll, R. J. (1976). "Zernike polynomials and atmospheric turbulence" (PDF). J. Opt. Soc. Am. 66 (3): 207. Bibcode:1976JOSA...66..207N. doi:10.1364/JOSA.66.000207.

[thibos2002-4] Thibos, L. N.; Applegate, R. A.; Schwiegerling, J. T.; Webb, R. (2002). "Standards for reporting the optical aberrations of eyes" (PDF). Journal of Refractive Surgery. 18 (5): S652–60.

[5] Genberg, V. L.; Michels, G. J.; Doyle, K. B. (2002). "Orthogonality of Zernike polynomials". Optomechanical design and Engineering 2002. Proc SPIE. 4771. pp. 276–286. doi:10.1117/12.482169.

[6] Lakshminarayanan, V.; Fleck, Andre (2011). "Zernike polynomials: a guide". J. Mod. Opt. 58 (7). pp. 545–561. Bibcode:2011JMOp...58..545L. doi:10.1080/09500340.2011.554896.

[barmak-7] Honarvar Shakibaei Asli, Barmak; Raveendran, Paramesran (July 2013). "Recursive formula to compute Zernike radial polynomials" Opt. Lett. (OSA) 38 (14): 2487–2489. doi:10.1364/OL.38.002487

[kintner1976-8] 1 2 Kintner, E. C. (1976). "On the mathematical properties of the Zernike Polynomials". Opt. Acta. 23 (8): 679–680. Bibcode:1976AcOpt..23..679K. doi:10.1080/713819334.

[9] Tatulli, E. (2013). "Transformation of Zernike coefficients: a Fourier-based method for scaled, translated, and rotated wavefront apertures". J. Opt. Soc. Am. A. 30 (4): 726–32. arXiv:1302.7106. Bibcode:2013JOSAA..30..726T. doi:10.1364/JOSAA.30.000726. PMID 23595334.

[10] Janssen, A. J. E. M. (2011). "New analytic results for the Zernike Circle Polynomials from a basic result in the Nijboer-Zernike diffraction theory". Journal of the European Optical Society: Rapid Publications. 6. doi:10.2971/jeos.2011.11028.

[11] Barakat, Richard (1980). "Optimum balanced wave-front aberrations for radially symmetric amplitude distributions: Generalizations of Zernike polynomials". J. Opt. Soc. Am. 70 (6): 739–742. Bibcode:1980JOSA...70..739B. doi:10.1364/JOSA.70.000739.

[12] Janssen, A. J. E. M. (2011). "A generalization of the Zernike circle polynomials for forward and inverse problems in diffraction theory". arXiv:1110.2369 [math-ph].

[13] Mathar, R. J. (2018). "Orthogonal basis function over the unit circle with the minimax property". arXiv:1802.09518 [math.NA].

[14] Tahmasbi, A. (2010). An Effective Breast Mass Diagnosis System using Zernike Moments. 17th Iranian Conf. on Biomedical Engineering (ICBME'2010). Isfahan, Iran: IEEE. pp. 1–4. doi:10.1109/ICBME.2010.5704941.

[15] Tahmasbi, A.; Saki, F.; Shokouhi, S.B. (2011). "Classification of Benign and Malignant Masses Based on Zernike Moments". Computers in Biology and Medicine. 41 (8): 726–735. doi:10.1016/j.compbiomed.2011.06.009. PMID 21722886.

[16] Rdzanek, W. P. (2018). "Sound radiation of a vibrating elastically supported circular plate embedded into a flat screen revisited using the Zernike circle polynomials". J. Sound Vibr. 434: 91–125. Bibcode:2018JSV...434...92R. doi:10.1016/j.jsv.2018.07.035.

[17] Alizadeh, Elaheh; Lyons, Samanthe M; Castle, Jordan M; Prasad, Ashok (2016). "Measuring systematic changes in invasive cancer cell shape using Zernike moments". Integrative Biology. 8 (11): 1183–1193. doi:10.1039/C6IB00100A. PMID 27735002.

Zernike polynomials

Definitions

Other representations

Noll's sequential indices

OSA/ANSI standard indices

Fringe/Zemax indices

Properties

Orthogonality

Zernike transform

Symmetries

Recurrence relations

Examples

Radial polynomials

Zernike polynomials

Applications

Higher dimensions

See also

References

External links