Natural logarithm of 2

The decimal value of the natural logarithm of 2 (sequence A002162 in the OEIS) is approximately

\ln(2)\approx 0.693\,147\,180\,56

as shown in the first line of the table below. The logarithm in other bases is obtained with the formula

\log_b(2) = \frac{\ln(2)}{\ln(b)}.

The common logarithm in particular is ( A007524)

\log _{10}(2)\approx 0.301\,029\,995\,663\,981\,195.

The inverse of this number is the binary logarithm of 10:

\log _{2}(10)={\frac {1}{\log _{10}(2)}}\approx 3.321\,928\,095

(

A020862).

number	approximate natural logarithm	OEIS
2	6999693147180559945♠0.693147180559945309417232121458	A002162
3	7000109861228866810♠1.09861228866810969139524523692	A002391
4	7000138629436111989♠1.38629436111989061883446424292	A016627
5	7000160943791243410♠1.60943791243410037460075933323	A016628
6	7000179175946922805♠1.79175946922805500081247735838	A016629
7	7000194591014905531♠1.94591014905531330510535274344	A016630
8	7000207944154167983♠2.07944154167983592825169636437	A016631
9	7000219722457733621♠2.19722457733621938279049047384	A016632
10	7000230258509299404♠2.30258509299404568401799145468	A002392

By the Lindemann–Weierstrass theorem, the natural logarithm of any natural number other than 0 and 1 (more generally, of any positive algebraic number other than 1) is a transcendental number.

It is not known whether ln (2) is a normal number.

Series representations

Rising alternate factorial

\ln(2)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-{\frac {1}{6}}+\cdots .

This is the well-known "alternating harmonic series".

\ln(2)={\tfrac {1}{2}}+{\tfrac {1}{2}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n(n+1)}}.

\ln(2)={\tfrac {5}{8}}+{\tfrac {1}{2}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n(n+1)(n+2)}}.

\ln(2)={\tfrac {2}{3}}+{\tfrac {3}{4}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n(n+1)(n+2)(n+3)}}.

\ln(2)={\tfrac {131}{192}}+{\tfrac {3}{2}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n(n+1)(n+2)(n+3)(n+4)}}.

\ln(2)={\tfrac {661}{960}}+{\tfrac {15}{4}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n(n+1)(n+2)(n+3)(n+4)(n+5)}}.

Binary rising constant factorial

\ln(2)=\sum _{n=1}^{\infty }{\frac {1}{2^{n}n}}.

\ln(2)=1-\sum _{n=1}^{\infty }{\frac {1}{2^{n}n(n+1)}}.

\ln(2)={\tfrac {1}{2}}+2\sum _{n=1}^{\infty }{\frac {1}{2^{n}n(n+1)(n+2)}}.

\ln(2)={\tfrac {5}{6}}-6\sum _{n=1}^{\infty }{\frac {1}{2^{n}n(n+1)(n+2)(n+3)}}.

\ln(2)={\tfrac {7}{12}}+24\sum _{n=1}^{\infty }{\frac {1}{2^{n}n(n+1)(n+2)(n+3)(n+4)}}.

\ln(2)={\tfrac {47}{60}}-120\sum _{n=1}^{\infty }{\frac {1}{2^{n}n(n+1)(n+2)(n+3)(n+4)(n+5)}}.

Other series representations

\sum _{n=0}^{\infty }{\frac {1}{(2n+1)(2n+2)}}=\ln(2).

\sum_{n=1}^\infty \frac{1}{n(4n^2-1)} = 2\ln(2) -1.

\sum_{n=1}^\infty \frac{(-1)^n}{n(4n^2-1)} = \ln(2) -1.

\sum _{n=1}^{\infty }{\frac {(-1)^{n}}{n(9n^{2}-1)}}=2\ln(2)-{\tfrac {3}{2}}.

\sum _{n=1}^{\infty }{\frac {1}{4n^{2}-2n}}=\ln(2).

\sum _{n=1}^{\infty }{\frac {2(-1)^{n+1}(2n-1)+1}{8n^{2}-4n}}=\ln(2).

\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{3n+1}}={\frac {\ln(2)}{3}}+{\frac {\pi }{3{\sqrt {3}}}}.

Involving the Riemann Zeta function

\sum _{n=2}^{\infty }{\frac {1}{2^{n}}}[\zeta (n)-1]=\ln(2)-{\tfrac {1}{2}}.

\sum_{n=1}^\infty \frac{1}{2n+1}[\zeta(n)-1] = 1-\gamma-\frac{\ln(2)}{2}.

\sum _{n=1}^{\infty }{\frac {1}{2^{2n-1}(2n+1)}}\zeta (2n)=1-\ln(2).

( $γ$ is the Euler–Mascheroni constant and $ζ$ Riemann's zeta function.)

BBP-type representations

\ln(2)={\tfrac {2}{3}}+{\tfrac {1}{2}}\sum _{k=1}^{\infty }\left({\frac {1}{2k}}+{\frac {1}{4k+1}}+{\frac {1}{8k+4}}+{\frac {1}{16k+12}}\right){\frac {1}{16^{k}}}.

(See more about Bailey–Borwein–Plouffe (BBP)-type representations.)

Applying the three general series for natural logarithm to 2 directly gives:

\ln(2)=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{n}}.

\ln(2)=\sum _{n=1}^{\infty }{\frac {1}{2^{n}n}}.

\ln(2)={\tfrac {2}{3}}\sum _{k=0}^{\infty }{\frac {1}{9^{k}(2k+1)}}.

Applying them to $\textstyle 2={\frac {3}{2}}\cdot {\frac {4}{3}}$ gives:

\ln(2)=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{2^{n}n}}+\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{3^{n}n}}.

\ln(2)=\sum _{n=1}^{\infty }{\frac {1}{3^{n}n}}+\sum _{n=1}^{\infty }{\frac {1}{4^{n}n}}.

\ln(2)={\frac {2}{5}}\sum _{k=0}^{\infty }{\frac {1}{25^{k}(2k+1)}}+{\frac {2}{7}}\sum _{k=0}^{\infty }{\frac {1}{49^{k}(2k+1)}}.

Applying them to $\textstyle 2=({\sqrt {2}})^{2}$ gives:

\ln(2)=2\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{({\sqrt {2}}+1)^{n}n}}.

\ln(2)=2\sum _{n=1}^{\infty }{\frac {1}{(2+{\sqrt {2}})^{n}n}}.

\ln(2)={\frac {4}{3+2{\sqrt {2}}}}\sum _{k=0}^{\infty }{\frac {1}{(17+12{\sqrt {2}})^{k}(2k+1)}}.

Applying them to $\textstyle 2={\left({\frac {16}{15}}\right)}^{7}\cdot {\left({\frac {81}{80}}\right)}^{3}\cdot {\left({\frac {25}{24}}\right)}^{5}$ gives:

\ln(2)=7\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{15^{n}n}}+3\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{80^{n}n}}+5\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{24^{n}n}}.

\ln(2)=7\sum _{n=1}^{\infty }{\frac {1}{16^{n}n}}+3\sum _{n=1}^{\infty }{\frac {1}{81^{n}n}}+5\sum _{n=1}^{\infty }{\frac {1}{25^{n}n}}.

\ln(2)={\frac {14}{31}}\sum _{k=0}^{\infty }{\frac {1}{961^{k}(2k+1)}}\,+\,{\frac {6}{161}}\sum _{k=0}^{\infty }{\frac {1}{25921^{k}(2k+1)}}\,+\,{\frac {10}{49}}\sum _{k=0}^{\infty }{\frac {1}{2401^{k}(2k+1)}}.

Representation as integrals

\int_0^1 \frac{dx}{1+x} = \ln(2),\text{ or, equivalently, }\int_1^2 \frac{dx}{x} = \ln(2).

\int_1^\infty \frac{dx}{(1+x^2)(1+x)^2} = \frac{1-\ln(2)}{4}.

\int_0^\infty \frac{dx}{1+e^{nx}} = \frac{\ln(2)}{n}; \int_0^\infty \frac{dx}{3+e^{nx}} = \frac{2\ln(2)}{3n}.

\int_0^\infty \frac{1}{e^x-1}-\frac{2}{e^{2x}-1}\,dx=\ln(2).

\int_0^\infty e^{-x}\frac{1-e^{-x}}{x} \, dx= \ln(2).

\int_0^1 \ln\left(\frac{x^2-1}{x\ln(x)}\right)dx=-1+\ln(2)+\gamma.

\int_0^\frac{\pi}{3} \tan(x) \, dx=2\int_0^\frac{\pi}{4} \tan(x) \, dx=\ln(2).

\int_{-\frac{\pi}{4}}^\frac{\pi}{4} \ln\left(\sin(x)+\cos(x)\right)\,dx=-\frac{\pi \ln(2)}{4}.

\int_0^1 x^2\ln(1+x)\,dx=\frac{2\ln(2)}{3}-\frac{5}{18}.

\int _{0}^{1}x\ln(1+x)\ln(1-x)\,dx={\tfrac {1}{4}}-\ln(2).

\int _{0}^{1}x^{3}\ln(1+x)\ln(1-x)\,dx={\tfrac {13}{96}}-{\frac {2\ln(2)}{3}}.

\int_0^1 \frac{\ln x}{(1+x)^2}\,dx = -\ln(2).

\int_0^1 \frac{\ln(1+x)-x}{x^2}\,dx=1-2\ln(2).

\int_0^1 \frac{dx}{x(1-\ln(x))(1-2\ln(x))} = \ln(2).

\int _{1}^{\infty }{\frac {\ln \left(\ln(x)\right)}{x^{3}}}\,dx=-{\frac {\gamma +\ln(2)}{2}}.

( $γ$ is the Euler–Mascheroni constant.)

Other representations

The Pierce expansion is A091846

\ln(2)=1-{\frac {1}{1\cdot 3}}+{\frac {1}{1\cdot 3\cdot 12}}-\cdots .

The Engel expansion is A059180

\ln(2) = \frac{1}{2} + \frac{1}{2\cdot 3} + \frac{1}{2\cdot 3\cdot 7} + \frac{1}{2\cdot 3\cdot 7\cdot 9}+\cdots.

The cotangent expansion is A081785

\ln(2) = \cot({\arccot(0) -\arccot(1) + \arccot(5) - \arccot(55) + \arccot(14187) -\cdots}).

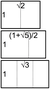
The simple continued fraction expansion is A016730

\ln(2)=\left[0;1,2,3,1,6,3,1,1,2,1,1,1,1,3,10,1,1,1,2,1,1,1,1,3,2,3,1,...\right]

,

which yields rational approximations, the first few of which are 0, 1, 2/3, 7/10, 9/13 and 61/88.

This generalized continued fraction:

\ln(2)=\left[0;1,2,3,1,5,{\tfrac {2}{3}},7,{\tfrac {1}{2}},9,{\tfrac {2}{5}},...,2k-1,{\frac {2}{k}},...\right]

,^[1]

also expressible as

\ln(2) = \cfrac{1} {1+\cfrac{1} {2+\cfrac{1} {3+\cfrac{2} {2+\cfrac{2} {5+\cfrac{3} {2+\cfrac{3} {7+\cfrac{4} {2+\ddots}}}}}}}} = \cfrac{2} {3-\cfrac{1^2} {9-\cfrac{2^2} {15-\cfrac{3^2} {21-\ddots}}}}

Bootstrapping other logarithms

Given a value of $ln(2)$ , a scheme of computing the logarithms of other integers is to tabulate the logarithms of the prime numbers and in the next layer the logarithms of the composite numbers $c$ based on their factorizations

c=2^{i}3^{j}5^{k}7^{l}\cdots \rightarrow \ln(c)=i\ln(2)+j\ln(3)+k\ln(5)+l\ln(7)+\cdots

Apart from the logarithms of 2, 3, 5 and 7 shown above, this employs

prime	approximate natural logarithm	OEIS
11	7000239789527279837♠2.39789527279837054406194357797	A016634
13	7000256494935746153♠2.56494935746153673605348744157	A016636
17	7000283321334405621♠2.83321334405621608024953461787	A016640
19	7000294443897916644♠2.94443897916644046000902743189	A016642
23	7000313549421592914♠3.13549421592914969080675283181	A016646
29	7000336729582998647♠3.36729582998647402718327203236	A016652
31	7000343398720448514♠3.43398720448514624592916432454	A016654
37	7000361091791264422♠3.61091791264422444436809567103	A016660
41	7000371357206670430♠3.71357206670430780386676337304	A016664
43	7000376120011569356♠3.76120011569356242347284251335	A016666
47	7000385014760171005♠3.85014760171005858682095066977	A016670
53	7000397029191355212♠3.97029191355212183414446913903	A016676
59	7000407753744390572♠4.07753744390571945061605037372	A016682
61	7000411087386417331♠4.11087386417331124875138910343	A016684
67	7000420469261939096♠4.20469261939096605967007199636	A016690
71	7000426267987704131♠4.26267987704131542132945453251	A016694
73	7000429045944114839♠4.29045944114839112909210885744	A016696
79	7000436944785246702♠4.36944785246702149417294554148	A016702
83	7000441884060779659♠4.41884060779659792347547222329	A016706
89	7000448863636973213♠4.48863636973213983831781554067	A016712
97	7000457471097850338♠4.57471097850338282211672162170	A016720

In a third layer, the logarithms of rational numbers $r = a / b$ are computed with $ln(r) = ln(a) - ln(b)$ , and logarithms of roots via $ln n \sqrt c = 1 / n ln(c)$ .

The logarithm of 2 is useful in the sense that the powers of 2 are rather densely distributed; finding powers $2 i$ close to powers $b j$ of other numbers $b$ is comparatively easy, and series representations of $ln(b)$ are found by coupling 2 to $b$ with logarithmic conversions.

Example

If $p s = q t + d$ with some small $d$ , then $p s / q t = 1 + d / q t$ and therefore

s\ln(p)-t\ln(q)=\ln \left(1+{\frac {d}{q^{t}}}\right)=\sum _{m=1}^{\infty }(-1)^{m+1}{\frac {({\frac {d}{q^{t}}})^{m}}{m}}=\sum _{n=0}^{\infty }{\frac {2}{2n+1}}{\left({\frac {d}{2q^{t}+d}}\right)}^{2n+1}.

Selecting $q = 2$ represents $ln(p)$ by $ln(2)$ and a series of a parameter $d / q t$ that one wishes to keep small for quick convergence. Taking $32 = 2 3 + 1$ , for example, generates

2\ln(3)=3\ln(2)-\sum _{k\geq 1}{\frac {(-1)^{k}}{8^{k}k}}=3\ln(2)+\sum _{n=0}^{\infty }{\frac {2}{2n+1}}{\left({\frac {1}{2\cdot 8+1}}\right)}^{2n+1}.

This is actually the third line in the following table of expansions of this type:

$s$	$p$	$t$	$q$	$d / q t$
1	3	1	2	1/2 = −6999500000000000000♠0.50000000…
1	3	2	2	−1/4 = −6999250000000000000♠0.25000000…
2	3	3	2	1/8 = −6999125000000000000♠0.12500000…
5	3	8	2	−13/256 = −6998507812500000000♠0.05078125…
12	3	19	2	7153/7005524288000000000♠524288 = −6998136432600000000♠0.01364326…
1	5	2	2	1/4 = −6999250000000000000♠0.25000000…
3	5	7	2	−3/128 = −6998234375000000000♠0.02343750…
1	7	2	2	3/4 = −6999750000000000000♠0.75000000…
1	7	3	2	−1/8 = −6999125000000000000♠0.12500000…
5	7	14	2	423/7004163840000000000♠16384 = −6998258178700000000♠0.02581787…
1	11	3	2	3/8 = −6999375000000000000♠0.37500000…
2	11	7	2	−7/128 = −6998546875000000000♠0.05468750…
11	11	38	2	7010104337636670000♠10433763667/7011274877906944000♠274877906944 = −6998379578100000000♠0.03795781…
1	13	3	2	5/8 = −6999625000000000000♠0.62500000…
1	13	4	2	−3/16 = −6999187500000000000♠0.18750000…
3	13	11	2	149/2048 = −6998727539100000000♠0.07275391…
7	13	26	2	−7006436034700000000♠4360347/7007671088640000000♠67108864 = −6998649742300000000♠0.06497423…
10	13	37	2	7008419538377000000♠419538377/7011137438953472000♠137438953472 = −6997305254000000000♠0.00305254…
1	17	4	2	1/16 = −6998625000000000000♠0.06250000…
1	19	4	2	3/16 = −6999187500000000000♠0.18750000…
4	19	17	2	−751/7005131072000000000♠131072 = −6997572968000000000♠0.00572968…
1	23	4	2	7/16 = −6999437500000000000♠0.43750000…
1	23	5	2	−9/32 = −6999281250000000000♠0.28125000…
2	23	9	2	17/512 = −6998332031200000000♠0.03320312…
1	29	4	2	13/16 = −6999812500000000000♠0.81250000…
1	29	5	2	−3/32 = −6998937500000000000♠0.09375000…
7	29	34	2	7007700071250000000♠70007125/7010171798691840000♠17179869184 = −6997407495000000000♠0.00407495…
1	31	5	2	−1/32 = −6998312500000000000♠0.03125000…
1	37	5	2	5/32 = −6999156250000000000♠0.15625000…
4	37	21	2	−7005222991000000000♠222991/7006209715200000000♠2097152 = −6999106330390000000♠0.10633039…
5	37	26	2	7006223509300000000♠2235093/7007671088640000000♠67108864 = −6998333054800000000♠0.03330548…
1	41	5	2	9/32 = −6999281250000000000♠0.28125000…
2	41	11	2	−367/2048 = −6999179199220000000♠0.17919922…
3	41	16	2	3385/7004655360000000000♠65536 = −6998516510000000000♠0.05165100…
1	43	5	2	11/32 = −6999343750000000000♠0.34375000…
2	43	11	2	−199/2048 = −6998971679700000000♠0.09716797…
5	43	27	2	7007127907150000000♠12790715/7008134217728000000♠134217728 = −6998952982500000000♠0.09529825…
7	43	38	2	−7009305929583700000♠3059295837/7011274877906944000♠274877906944 = −6998111296500000000♠0.01112965…

Starting from the natural logarithm of $q = 10$ one might use these parameters:

$s$	$p$	$t$	$q$	$d / q t$
10	2	3	10	3/125 = −6998240000000000000♠0.02400000…
21	3	10	10	7008460353203000000♠460353203/7010100000000000000♠10000000000 = −6998460353200000000♠0.04603532…
3	5	2	10	1/4 = −6999250000000000000♠0.25000000…
10	5	7	10	−3/128 = −6998234375000000000♠0.02343750…
6	7	5	10	7004176490000000000♠17649/7005100000000000000♠100000 = −6999176490000000000♠0.17649000…
13	7	11	10	−7009311098959300000♠3110989593/7011100000000000000♠100000000000 = −6998311099000000000♠0.03110990…
1	11	1	10	1/10 = −6999100000000000000♠0.10000000…
1	13	1	10	3/10 = −6999300000000000000♠0.30000000…
8	13	9	10	−7008184269279000000♠184269279/7009100000000000000♠1000000000 = −6999184269280000000♠0.18426928…
9	13	10	10	7008604499373000000♠604499373/7010100000000000000♠10000000000 = −6998604499400000000♠0.06044994…
1	17	1	10	7/10 = −6999700000000000000♠0.70000000…
4	17	5	10	−7004164790000000000♠16479/7005100000000000000♠100000 = −6999164790000000000♠0.16479000…
9	17	11	10	7010185878764970000♠18587876497/7011100000000000000♠100000000000 = −6999185878760000000♠0.18587876…
3	19	4	10	−3141/7004100000000000000♠10000 = −6999314100000000000♠0.31410000…
4	19	5	10	7004303210000000000♠30321/7005100000000000000♠100000 = −6999303210000000000♠0.30321000…
7	19	9	10	−7008106128261000000♠106128261/7009100000000000000♠1000000000 = −6999106128260000000♠0.10612826…
2	23	3	10	−471/1000 = −6999471000000000000♠0.47100000…
3	23	4	10	2167/7004100000000000000♠10000 = −6999216700000000000♠0.21670000…
2	29	3	10	−159/1000 = −6999159000000000000♠0.15900000…
2	31	3	10	−39/1000 = −6998390000000000000♠0.03900000…

References

Brent, Richard P. (1976). "Fast multiple-precision evaluation of elementary functions". J. ACM. 23 (2): 242–251. doi:10.1145/321941.321944. MR 0395314.
Uhler, Horace S. (1940). "Recalculation and extension of the modulus and of the logarithms of 2, 3, 5, 7 and 17". Proc. Natl. Acad. Sci. U.S.A. 26: 205–212. doi:10.1073/pnas.26.3.205. MR 0001523. PMC 1078033. PMID 16588339.
Sweeney, Dura W. (1963). "On the computation of Euler's constant". Mathematics of Computation. 17: 170–178. doi:10.1090/S0025-5718-1963-0160308-X. MR 0160308.
Chamberland, Marc (2003). "Binary BBP-formulae for logarithms and generalized Gaussian–Mersenne primes" (PDF). Journal of Integer Sequences. 6: 03.3.7. MR 2046407.
Gourévitch, Boris; Guillera Goyanes, Jesús (2007). "Construction of binomial sums for $π$ and polylogarithmic constants inspired by BBP formulas" (PDF). Applied Math. E-Notes. 7: 237–246. MR 2346048.
Wu, Qiang (2003). "On the linear independence measure of logarithms of rational numbers". Mathematics of Computation. 72 (242): 901–911. doi:10.1090/S0025-5718-02-01442-4.

↑ Borwein, J.; Crandall, R.; Free, G. (2004). "On the Ramanujan AGM Fraction , I: The Real-Parameter Case" (PDF). Exper. Math. 13 (3): 278–280. doi:10.1080/10586458.2004.10504540.

External links

Weisstein, Eric W. "Natural logarithm of 2". MathWorld.
"table of natural logarithms". PlanetMath.
Gourdon, Xavier; Sebah, Pascal. "The logarithm constant:log 2".

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Borwein, J.; Crandall, R.; Free, G. (2004). "On the Ramanujan AGM Fraction , I: The Real-Parameter Case" (PDF). Exper. Math. 13 (3): 278–280. doi:10.1080/10586458.2004.10504540.

Irrational numbers
Prime ( $ρ$ ) Logarithm of 2 Twelfth root of two (¹²√2) Apéry's ( $ζ (3)$ ) Plastic ( $ρ$ ) Square root of 2 (√2) Erdős–Borwein ( $E$ ) Golden ratio ( $φ$ ) Square root of 3 (√3) Square root of 5 (√5) Silver ratio ( $δ S$ ) Euler's ( $e$ ) Pi ( $π$ )
Schizophrenic Transcendental Trigonometric