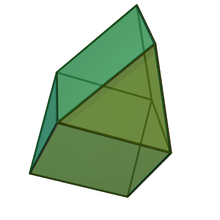
Gyrobifastigium

Gyrobifastigium
Type Johnson
J25 - J26 - J27
Faces 4 triangles
4 squares
Edges 14
Vertices 8
Vertex configuration 4(3.42)
4(3.4.3.4)
Symmetry group D2d
Dual polyhedron Elongated tetragonal disphenoid
Properties convex, honeycomb
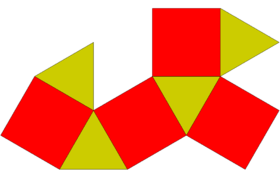
Net

In geometry, the gyrobifastigium is the 26th Johnson solid (J26). It can be constructed by joining two face-regular triangular prisms along corresponding square faces, giving a quarter-turn to one prism.[1] It is the only Johnson solid that can tile three-dimensional space.[2][3]

History and name

A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[4]

The name of the gyrobifastigium comes from the Latin fastigium, meaning a sloping roof.[5] In the standard naming convention of the Johnson solids, bi- means two solids connected at their bases, and gyro- means the two halves are twisted with respect to each other.

The gyrobifastigium's place in the list of Johnson solids, immediately before the bicupolas, is explained by viewing it as a digonal gyrobicupola. Just as the other regular cupolas have an alternating sequence of squares and triangles surrounding a single polygon at the top (triangle, square or pentagon), each half of the gyrobifastigium consists of just alternating squares and triangles, connected at the top only by a ridge.

Honeycomb

The gyrated triangular prismatic honeycomb can be constructed by packing together large numbers of identical gyrobifastigiums. The gyrobifastigium is one of five convex polyhedra with regular faces capable of space-filling (the others being the cube, truncated octahedron, triangular prism, and hexagonal prism) and it is the only Johnson solid capable of doing so.[2][3]

Formulae

The following formulae for volume and surface area can be used if all faces are regular, with edge length a:

Topologically equivalent polyhedra

Schmitt–Conway–Danzer biprism

Schmitt–Conway–Danzer biprism

The Schmitt–Conway–Danzer biprism (also called a SCD prototile[6]) is a polyhedron topologically equivalent to the gyrobifastigium, but with parallelogram and irregular triangle faces instead of squares and equilateral triangles. Like the gyrobifastigium, it can fill space, but only aperiodically or with a screw symmetry, not with a full three-dimensional group of symmetries. Thus, it provides a partial solution to the three-dimensional einstein problem.[7][8]

Dual of gyrobifastigium

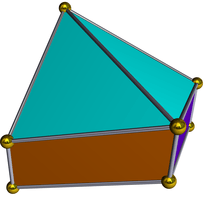
The dual polyhedron of the gyrobifastigium has 8 faces: 4 isosceles triangles, corresponding to the degree-three vertices of the gyrobifastigium, and 4 parallelograms corresponding to the degree-four equatorial vertices.

Elongated digonal gyrobicupola

The related elongated digonal gyrobicupola is formed by augmenting two triangular prisms to a central cube. The elongated digonal gyrobicupola can self-tessellate space. With regular faces, it has 4 sets of coplanar adjacent squares and triangles. The triangles and squares can be combined together as pentagons.


elongated digonal gyrobicupola

Bifastigium

Gyrobifastigium
Faces 4 triangles
4 trapezoids
Edges 14
Vertices 8
Symmetry group D2h
Dual polyhedron self-dual
Properties convex

The bifastigium (digonal orthobicupola), is formed by gluing together two triangular prisms on their square faces, but without twisting. It is topologically a self-dual polyhedron and can also be called an elongated octahedron and self-dual octahedron.[9]

These polyhedra resemble the dual gyrobifastigium in that both shapes have eight vertices and eight faces, with the faces forming a belt of four quadrilaterals separating two pairs of triangles from each other. However, in the dual gyrobifastigium the two pairs of triangles are twisted with respect to each other while in the bifastigium they are not.

It can be made with regular faces, squares and triangles, but the triangles will be coplanar.

References

  1. ↑ Darling, David (2004), The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, John Wiley & Sons, p. 169, ISBN 9780471667001 .
  2. 1 2 Alam, S. M. Nazrul; Haas, Zygmunt J. (2006), "Coverage and Connectivity in Three-dimensional Networks", Proceedings of the 12th Annual International Conference on Mobile Computing and Networking (MobiCom '06), New York, NY, USA: ACM, pp. 346–357, arXiv:cs/0609069, doi:10.1145/1161089.1161128, ISBN 1-59593-286-0 .
  3. 1 2 Kepler, Johannes (2010), The Six-Cornered Snowflake, Paul Dry Books, Footnote 18, p. 146, ISBN 9781589882850 .
  4. ↑ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603 .
  5. ↑ Rich, Anthony (1875), "Fastigium", in Smith, William, A Dictionary of Greek and Roman Antiquities, London: John Murray, pp. 523–524 .
  6. ↑ Forcing Nonperiodicity With a Single Tile Joshua E. S. Socolar and Joan M. Taylor, 2011
  7. ↑ Senechal, Marjorie (1996), "7.2 The SCD (Schmitt–Conway–Danzer) tile", Quasicrystals and Geometry, Cambridge University Press, pp. 209–213, ISBN 9780521575416 .
  8. ↑ Tiling Space with a Schmitt-Conway Biprism wolfram demonstrations
  9. ↑ http://dmccooey.com/polyhedra/SelfDualOctahedron2.html
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.