Flower snark
| Flower snark | |
|---|---|
 The flower snarks J3, J5 and J7. | |
| Vertices | 4n |
| Edges | 6n |
| Girth |
3 for n=3 5 for n=5 6 for n≥7 |
| Chromatic number | 3 |
| Chromatic index | 4 |
| Book thickness |
3 for n=5 3 for n=7 |
| Queue number |
2 for n=5 2 for n=7 |
| Properties | Snark for n≥5 |
| Notation | Jn with n odd |
| Table of graphs and parameters | |
| Flower snark J5 | |
|---|---|
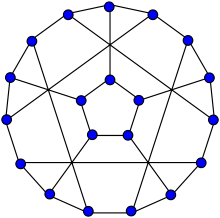 The flower snark J5. | |
| Vertices | 20 |
| Edges | 30 |
| Girth | 5 |
| Chromatic number | 3 |
| Chromatic index | 4 |
| Properties |
Snark Hypohamiltonian |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.[1]
As snarks, the flower snarks are connected, bridgeless cubic graphs with chromatic index equal to 4. The flower snarks are non-planar and non-hamiltonian. The flower snarks J5 and J7 have book thickness 3 and queue number 2.[2]
Construction
The flower snark Jn can be constructed with the following process :
- Build n copies of the star graph on 4 vertices. Denote the central vertex of each star Ai and the outer vertices Bi, Ci and Di. This results in a disconnected graph on 4n vertices with 3n edges (Ai – Bi, Ai – Ci and Ai – Di for 1 ≤ i ≤ n).
- Construct the n-cycle (B1... Bn). This adds n edges.
- Finally construct the 2n-cycle (C1... CnD1... Dn). This adds 2n edges.
By construction, the Flower snark Jn is a cubic graph with 4n vertices and 6n edges. For it to have the required properties, n should be odd.
Special cases
The name flower snark is sometimes used for J5, a flower snark with 20 vertices and 30 edges.[3] It is one of 6 snarks on 20 vertices (sequence A130315 in the OEIS). The flower snark J5 is hypohamiltonian.[4]
J3 is a trivial variation of the Petersen graph formed by replacing one of its vertices by a triangle. This graph is also known as the Tietze's graph.[5] In order to avoid trivial cases, snarks are generally restricted to have girth at least 5. With that restriction, J3 is not a snark.
Gallery
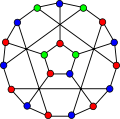 The chromatic number of the flower snark J5 is 3.
The chromatic number of the flower snark J5 is 3. The chromatic index of the flower snark J5 is 4.
The chromatic index of the flower snark J5 is 4. The original representation of the flower snark J5.
The original representation of the flower snark J5.
References
- ↑ Isaacs, R. "Infinite Families of Nontrivial Trivalent Graphs Which Are Not Tait Colorable." Amer. Math. Monthly 82, 221–239, 1975.
- ↑ Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- ↑ Weisstein, Eric W. "Flower Snark". MathWorld.
- ↑ Weisstein, Eric W. "Hypohamiltonian Graph". MathWorld.
- ↑ Clark, L.; Entringer, R. (1983), "Smallest maximally nonhamiltonian graphs", Periodica Mathematica Hungarica, 14 (1): 57–68, doi:10.1007/BF02023582 .