If you have programmed in any other language before, you likely wrote some functions that "kept state". For those new to the concept, a state is one or more variables that are required to perform some computation but are not among the arguments of the relevant function. Object-oriented languages like C++ make extensive use of state variables (in the form of member variables inside classes and objects). Procedural languages like C on the other hand typically use global variables declared outside the current scope or static variables in the functions to keep track of state.
In Haskell, however, such techniques are not as straightforward to apply. Doing so will require mutable variables which would mean that functions will have hidden dependencies, which is at odds with Haskell's functional purity. Fortunately, often it is possible to keep track of state in a functionally pure way. We do so by passing the state information from one function to the next, thus making the hidden dependencies explicit. The State type is designed to simplify this process of threading state through functions. In this chapter, we will see how it can assist us in a typical problem involving state: generating pseudo-random numbers.
Pseudo-Random Numbers
Generating actual random numbers is hard. Computer programs almost always use pseudo-random numbers instead. They are "pseudo" because they are not actually random, and that they are known in advance. Indeed, they are generated by algorithms (the pseudo-random number generators) which take an initial state (commonly called the seed) and produce from it a sequence of numbers that have the appearance of being random.[1] Every time a pseudo-random number is requested, state somewhere must be updated, so that the generator can be ready for producing a fresh, different random number the next time. Sequences of pseudo-random numbers can be replicated exactly if the initial seed and the generating algorithm are known.
Implementation in Haskell
Producing a pseudo-random number in most programming languages is very simple: there is a function somewhere in the libraries that provides a pseudo-random value (perhaps even a truly random one, depending on how it is implemented). Haskell has a similar one in the System.Random module from the random package:
GHCi> :m System.Random
GHCi> :t randomIO
randomIO :: Random a => IO a
GHCi> randomIO
-1557093684
GHCi> randomIO
1342278538
randomIO is an IO action. It couldn't be otherwise, as it makes use of mutable state, which is kept out of reach from our Haskell programs. Thanks to this hidden dependency, the pseudo-random values it gives back can be different every time.
Example: Rolling Dice

randomRIO (1,6)Suppose we are coding a game in which at some point we need an element of chance. In real-life games that is often obtained by means of dice. So, let's create a dice-throwing function. We'll use the IO function randomRIO, which allows us to specify a range from which the pseudo-random values will be taken. For a 6 die, the call will be randomRIO (1,6).
import Control.Applicative
import System.Random
rollDiceIO :: IO (Int, Int)
rollDiceIO = liftA2 (,) (randomRIO (1,6)) (randomRIO (1,6))
That function rolls two dice. Here, liftA2 is used to make the two-argument function (,) work within a monad or applicative functor, in this case IO.[2] It can be easily defined in terms of (<*>):
liftA2 f u v = f <$> u <*> v
As for (,), it is the non-infix version of the tuple constructor. That being so, the two die rolls will be returned as a tuple in IO.
| Exercises |
|---|
|
Getting Rid of IO
A disadvantage of randomIO is that it requires us to use IO and store our state outside the program, where we can't control what happens to it. We would rather only use I/O when there is an unavoidable reason to interact with the outside world.
To avoid bringing IO into play, we can build a local generator. The random and mkStdGen functions in System.Random allow us to generate tuples containing a pseudo-random number together with an updated generator to use the next time the function is called.
GHCi> :m System.Random
GHCi> let generator = mkStdGen 0 -- "0" is our seed
GHCi> :t generator
generator :: StdGen
GHCi> generator
1 1
GHCi> :t random
random :: (RandomGen g, Random a) => g -> (a, g)
GHCi> random generator :: (Int, StdGen)
(2092838931,1601120196 1655838864)
Note
In random generator :: (Int, StdGen), we use the :: to introduce a type annotation, which is essentially a type signature that we can put in the middle of an expression. Here, we are saying that the expression random generator has type (Int, StdGen). It makes sense to use a type annotation here because, as we will discuss later, random can produce values of different types, so if we want it to give us an Int we'd better specify it in some way.
While we managed to avoid IO, there are new problems. First and foremost, if we want to use generator to get random numbers, the obvious definition...
GHCi> let randInt = fst . random $ generator :: Int
GHCi> randInt
2092838931
... is useless. It will always give back the same value, 2092838931, as the same generator in the same state will be used every time. To solve that, we can take the second member of the tuple (that is, the new generator) and feed it to a new call to random:
GHCi> let (randInt, generator') = random generator :: (Int, StdGen)
GHCi> randInt -- Same value
2092838931
GHCi> random generator' :: (Int, StdGen) -- Using new generator' returned from “random generator”
(-2143208520,439883729 1872071452)
That, of course, is clumsy and rather tedious, as we now need to deal with the fuss of carefully passing the generator around.
Dice without IO
We can re-do our dice throw with our new approach using the randomR function (which is the generator version of our rollDiceIO function above):
GHCi> randomR (1,6) (mkStdGen 0)
(6, 40014 40692)
The resulting tuple combines the result of throwing a single die with a new generator. A simple implementation for throwing two dice is then:
clumsyRollDice :: (Int, Int)
clumsyRollDice = (n, m)
where
(n, g) = randomR (1,6) (mkStdGen 0)
(m, _) = randomR (1,6) g
| Exercises |
|---|
|
The implementation of clumsyRollDice works as a one-off, but we have to manually pass the generator g from one where clause to the other. This approach becomes increasingly cumbersome as our programs get more complex, which means we have more values to shift around. It is also error-prone: what if we pass one of the middle generators to the wrong line in the where clause?
What we really need is a way to automate the extraction of the second member of the tuple (i.e. the new generator) and feed it to a new call to random. This is where the State comes into the picture.
Introducing State
The Haskell type State describes functions that consume a state and produce both a result and an updated state, which are given back in a tuple.
The state function is wrapped by a data type definition which comes along with a runState accessor so that pattern matching becomes unnecessary. For our current purposes, the State type might be defined as:
newtype State s a = State { runState :: s -> (a, s) }
Here, s is the type of the state, and a the type of the produced result. Calling the type State is arguably a bit of a misnomer because the wrapped value is not the state itself but a state processor.
newtype
Note that we defined the data type with the newtype keyword, rather than the usual data. newtype can be used only for types with just one constructor and just one field. It ensures that the trivial wrapping and unwrapping of the single field is eliminated by the compiler. For that reason, simple wrapper types such as State are usually defined with newtype. Would defining a synonym with type be enough in such cases? Not really, because type does not allow us to define instances for the new data type, which is what we are about to do...
Where did the State constructor go?
In the wild, the State type is provided by Control.Monad.Trans.State in transformers (and is also reexported by Control.Monad.State in mtl). When you use it, you will quickly notice there is no State constructor available. The transformers package implements the State type in a different way. The differences do not affect how we use or understand State; except that, instead of a State constructor, Control.Monad.Trans.State exports a state function,
state :: (s -> (a, s)) -> State s a
which does the same job. As for why the actual implementation is not the obvious one we presented above, we will get back to that a few chapters down the road.
Instantiating the Monad
So far, all we have done was to wrap a function type and give it a name. There is another ingredient, however: for every type s, State s can be made a Monad instance, giving us very handy ways of using it.
To define a Monad instance, there must also be instances for Functor and Applicative. As we explained previously, these superclass instances can be derived as follows from the Monad instance that we are about to define in more detail.
instance Functor (State s) where
fmap = Control.Monad.liftM
instance Applicative (State s) where
pure = return
(<*>) = Control.Monad.ap
| Exercises |
|---|
|
So let's define this instance.
instance Monad (State s) where
Note the instance is State s, and not just State: on its own, State can't be made an instance of Monad, as it takes two type parameters, rather than one.
That means there are actually many different State monads, one for each possible type of state - State String, State Int, State SomeLargeDataStructure, and so forth. However, we only need to write one implementation of return and (>>=); the methods will be able to deal with all choices of s.
The return function is implemented as:
return :: a -> State s a
return x = state ( \ s -> (x, s) )
Giving a value (x) to return produces a function which takes a state (s) and returns it unchanged, together with the value we want to be returned. As a finishing step, the function is wrapped up with the state function.
As for binding, it can be defined like this:
(>>=) :: State s a -> (a -> State s b) -> State s b
p >>= k = q where
p' = runState p -- p' :: s -> (a, s)
k' = runState . k -- k' :: a -> s -> (b, s)
q' s0 = (y, s2) where -- q' :: s -> (b, s)
(x, s1) = p' s0 -- (x, s1) :: (a, s)
(y, s2) = k' x s1 -- (y, s2) :: (b, s)
q = state q'
We wrote the definition above in a quite verbose way, to make the steps involved easier to pinpoint. A more compact way of writing it would be:
p >>= k = state $ \ s0 ->
let (x, s1) = runState p s0 -- Running the first processor on s0.
in runState (k x) s1 -- Running the second processor on s1.
(>>=) is given a state processor (p) and a function (k) that is used to create another processor from the result of the first one. The two processors are combined into a function that takes the initial state (s) and returns the second result and the third state (i.e. the output of the second processor). Overall, (>>=) here allows us to run two state processors in sequence, while allowing the result of the first stage to influence what happens in the second one.
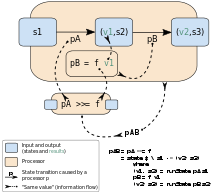
pAB) from a state processor (pA) and a processor-making function (f). s1, s2 and s3 are states. v1 and v2 are values. pA, pB and pAB are state processors. The wrapping and unwrapping by State/runState is implicit.One detail in the implementation is how runState is used to undo the State wrapping, so that we can reach the function that will be applied to the states. The type of runState p, for instance, is s -> (a, s).
Another way to understand this derivation of the bind operator >>= is to consider once more the explicit but cumbersome way to simulate a stateful function of type a -> b by using functions of type (a, s) -> (b, s) , or, said another way: a -> s -> (b,s) = a -> (s -> (b,s)). These classes of functions pass the state on from function to function. Note that this last signature already suggests the right-hand side type in a bind operation where the abstract type is S b = (s -> (b, s)).
Now that we have seen how the types seem to suggest the monadic signatures, lets consider a much more concrete question: Given two functions f :: s -> (a, s) and g :: a -> s -> (b, s), how do we chain them to produce a new function that passes on the intermediate state?
This question does not require thinking about monads: one option is to simply use function composition. It helps our exposition if we just write it down explicitly as a lambda expression:
compose :: (s -> (a,s)) -> {- first function -}
(a -> (s -> (b,s))) -> {- second function, note type is similar to (a,s) -> (b,s) -}
s -> (b,s) {- composed function -}
compose f g = \s0 -> let (a1, s1) = f s0 in (g a1) s1
{-This lambda expression threads both intermediate results produced by f into those required by g -}
Now, if in addition to chaining the input functions, we find that the functions of signature s -> (a,s) were all wrapped in an abstract datatype Wrapped a, and that therefore we need to call some other provided functionswrap :: (s -> (a,s)) -> Wrapped a, and unwrap :: Wrapped a -> (s -> (a,s)) in order to get to the inner function, then the code changes slightly:
{- what happens if the type s -> (a,s) is wrapped and this new type is called Wrapped a -}
composeWrapped :: Wrapped a -> (a -> Wrapped b) -> Wrapped b
composeWrapped wrappedf g = wrap (\s0 -> let (a1,s1) = (unwrap wrappedf) s0 in (unwrap (g a1)) s1)
This code is the implementation of (>>=) shown above, with wrap = state and unwrap = runState, so we can now see how the definition of bind given earlier is the standard function composition for this special kind of stateful function.
This explanation does not address yet where the original functions Wrapped a and a -> Wrapped b come from in the first place, but they do explain what you can do with them once you have them.
Setting and Accessing the State
The monad instance allows us to manipulate various state processors, but you may at this point wonder where exactly the original state comes from in the first place. That issue is handily dealt with by the function put:
put newState = state $ \_ -> ((), newState)
Given a state (the one we want to introduce), put generates a state processor which ignores whatever state it receives, and gives back the state we originally provided to put. Since we don't care about the result of this processor (all we want to do is to replace the state), the first element of the tuple will be (), the universal placeholder value.[3]
As a counterpart to put, there is get:
get = state $ \s -> (s, s)
The resulting state processor gives back the state s it is given in both as a result and as a state. That means the state will remain unchanged, and that a copy of it will be made available for us to manipulate.
Getting Values and State
As we have seen in the implementation of (>>=), runState is used to unwrap the State s a value to get the actual state processing function, which is then applied to some initial state. Other functions which are used in similar ways are evalState and execState.
Given a State a b and an initial state, the function evalState will give back only the result value of the state processing, whereas execState will give back just the new state.
evalState :: State s a -> s -> a
evalState p s = fst (runState p s)
execState :: State s a -> s -> s
execState p s = snd (runState p s)
Dice and state
Time to use the State monad for our dice throw examples.
import Control.Monad.Trans.State
import System.Random
We want to generate Int dice throw results from a pseudo-random generator of type StdGen. Therefore, the type of our state processors will be State StdGen Int, which is equivalent to StdGen -> (Int, StdGen) bar the wrapping.
We can now implement a processor that, given a StdGen generator, produces a number between 1 and 6. Now, the type of randomR is:
-- The StdGen type we are using is an instance of RandomGen.
randomR :: (Random a, RandomGen g) => (a, a) -> g -> (a, g)
Doesn't it look familiar? If we assume a is Int and g is StdGen it becomes:
randomR (1, 6) :: StdGen -> (Int, StdGen)
We already have a state processing function! All that is missing is to wrap it with state:
rollDie :: State StdGen Int
rollDie = state $ randomR (1, 6)
For illustrative purposes, we can use get, put and do-notation to write rollDie in a very verbose way which displays explicitly each step of the state processing:
rollDie :: State StdGen Int
rollDie = do generator <- get
let (value, newGenerator) = randomR (1,6) generator
put newGenerator
return value
Let's go through each of the steps:
- First, we take out the pseudo-random generator from the monadic context with
<-, so that we can manipulate it. - Then, we use the
randomRfunction to produce an integer between 1 and 6 using the generator we took. We also store the new generator graciously returned byrandomR. - We then set the state to be the
newGeneratorusingput, so that any furtherrandomRin the do-block, or further on in a(>>=)chain, will use a different pseudo-random generator. - Finally, we inject the result back into the
State StdGenmonad usingreturn.
We can finally use our monadic die. As before, the initial generator state itself is produced by the mkStdGen function.
GHCi> evalState rollDie (mkStdGen 0)
6
Why have we involved monads and built such an intricate framework only to do exactly what fst . randomR (1,6) already does? Well, consider the following function:
rollDice :: State StdGen (Int, Int)
rollDice = liftA2 (,) rollDie rollDie
We obtain a function producing two pseudo-random numbers in a tuple. Note that these are in general different:
GHCi> evalState rollDice (mkStdGen 666)
(6,1)
Under the hood, state is being passed through (>>=) from one rollDie computation to the other. Doing that was previously very clunky using randomR (1,6) alone because we had to pass state manually. Now, the monad instance is taking care of that for us. Assuming we know how to use the lifting functions, constructing intricate combinations of pseudo-random numbers (tuples, lists, whatever) has suddenly become much easier.
| Exercises |
|---|
|
Pseudo-random values of different types
Until now, we have used only Int as type of the value produced by the pseudo-random generator. However, looking at the type of randomR shows we are not restricted to Int. It can generate values of any type in the Random class from System.Random. There already are instances for Int, Char, Integer, Bool, Double and Float, so you can immediately generate any of those.
Because State StdGen is "agnostic" in regard to the type of the pseudo-random value it produces, we can write a similarly "agnostic" function that provides a pseudo-random value of unspecified type (as long as it is an instance of Random):
getRandom :: Random a => State StdGen a
getRandom = state random
Compared to rollDie, this function does not specify the Int type in its signature and uses random instead of randomR; otherwise, it is just the same. getRandom can be used for any instance of Random:
GHCi> evalState getRandom (mkStdGen 0) :: Bool
True
GHCi> evalState getRandom (mkStdGen 0) :: Char
'\64685'
GHCi> evalState getRandom (mkStdGen 0) :: Double
0.9872770354820595
GHCi> evalState getRandom (mkStdGen 0) :: Integer
2092838931
Indeed, it becomes quite easy to conjure all these at once:
someTypes :: State StdGen (Int, Float, Char)
someTypes = liftA3 (,,) getRandom getRandom getRandom
allTypes :: State StdGen (Int, Float, Char, Integer, Double, Bool, Int)
allTypes = (,,,,,,) <$> getRandom
<*> getRandom
<*> getRandom
<*> getRandom
<*> getRandom
<*> getRandom
<*> getRandom
For writing allTypes, there is no liftA7,[4] and so we resort to plain old (<*>) instead. Using it, we can apply the tuple constructor to each of the seven random values in the State StdGen monadic context.
allTypes provides pseudo-random values for all default instances of Random; an additional Int is inserted at the end to prove that the generator is not the same, as the two Ints will be different.
GHCi> evalState allTypes (mkStdGen 0)
GHCi>(2092838931,9.953678e-4,'\825586',-868192881,0.4188001483955421,False,316817438)
| Exercises |
|---|
|
Notes
- ↑ A common source of seeds is the current date and time as given by the internal clock of the computer. Assuming the clock is functioning correctly, it can provide unique seeds suitable for most day-to-day needs (as opposed to applications which demand high-quality randomness, as in cryptography or statistics).
- ↑ If you need a refresher on applicative functors, have a look at the first section of the Prologue.
- ↑ The technical term for both
()and its type is unit. - ↑ Beyond
liftA3, the standard libraries only provide the monad-onlyliftM4andliftM5inControl.Monad.