Dopplereffect
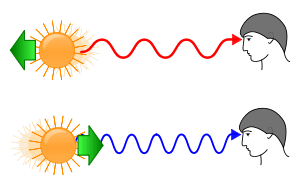
Het dopplereffect is de waargenomen verandering van frequentie van geluid, licht of andere golfverschijnselen, door een snelheidsverschil tussen de zender en de ontvanger.
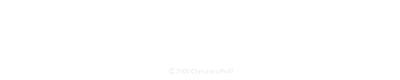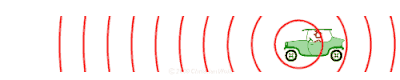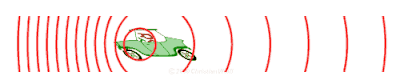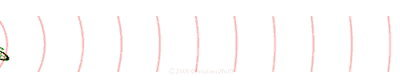
Ontdekking

Het effect werd genoemd naar de Oostenrijkse natuurkundige Christian Doppler, die in 1842 dit verschijnsel voor zowel licht- als geluidsgolven beschreef, in de verhandeling Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels. In 1845 werd het experimenteel getoetst door de Nederlandse meteoroloog Christophorus Buys Ballot. Hij deed dat door een groep hoornisten bij Utrecht in een open spoorwagon met hoge snelheid langs een groep waarnemers te laten rijden.
Na de opkomst van het wegverkeer is zo'n proefopstelling niet meer nodig om het dopplereffect bij geluid te constateren. Voor een (stilstaande) waarnemer daalt de toonhoogte van het geluid van een snel voorbijrijdend voertuig duidelijk tijdens het passeren. Het effect is vooral sterk bij uitrukkende voertuigen van de hulpdiensten, doordat deze met hoge snelheid rijden en de meertonige hoorns en sirenes een hard geluid op vaste toonhoogtes produceren.
Op een kort moment hoort de waarnemer de oorspronkelijke toonhoogte, namelijk op het moment dat de geluidsbron de waarnemer passeert.
Verklaring
Door een medium
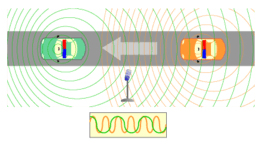

Het dopplereffect ontstaat doordat de bron (of de ontvanger) van de golven beweegt ten opzichte van het medium[1]. Voor golven die door een medium voortgeplant worden, zoals geluidsgolven, gelden de onderstaande formules[2]. Steeds wordt het medium in rust gedacht. Mocht het medium ook bewegen, zoals in een gasstroom, dan worden de snelheden relatief ten opzichte van het medium opgevat.
Het dopplereffect is te begrijpen door te bedenken dat de bron een reeks "golfjes" produceert met frequentie . De golven bewegen met een snelheid die bepaald wordt door het medium. Wanneer de bron een volgende golf produceert is hij zelf een stukje bewogen in de richting van de vorige golf. Hoe hoger de snelheid van de bron, hoe korter de afstand tussen de twee opeenvolgende golven (golflengte). Ook de tijd tussen twee golven in het medium (periode) wordt korter. Immers, als de bron de tweede golf produceert is hij niet meer op dezelfde plek als toen hij de eerste golf produceerde. De eerste golf had zelf ook enige tijd nodig om deze plek te bereiken. Aangezien de periode afneemt, neemt de frequentie toe met toenemende snelheid van de bron.
Door het dopplereffect veranderen golflengte en frequentie. Alleen de snelheid van de golf verandert niet. Immers, als de golf de bron verlaten heeft, heeft hij alleen nog met het medium te maken. Voor de waargenomen frequentie geldt:
met
- de frequentie van de golf die de bron uitzendt
- de voortplantingssnelheid van de golf in het medium, in lucht is dit de geluidssnelheid
- de snelheid waarmee de golfbron beweegt ten opzichte van het medium; positief als bron en waarnemer elkaar naderen; negatief als zij zich van elkaar verwijderen
- de snelheid waarmee de waarnemer beweegt ten opzichte van het medium; positief als bron en waarnemer elkaar naderen; negatief als zij zich van elkaar verwijderen.
Bovenstaande uitdrukking is geldig als de waarnemer en de bron bewegen over de directe lijn tussen bron en waarnemer. Dan is de frequentie bij nadering met een vaste waarde verhoogd en bij verwijdering met een vaste waarde verlaagd. In de praktijk zal de waarnemer zich meestal naast de baan van de bron bevinden. De relatieve snelheid van de bron zal dan van een aanvankelijk langzaam veranderende waarde, in de buurt van de waarnemer van een positieve waarde door 0 naar een negatieve waarde gaan. Bij een geluidsbron hoort de waarnemer een aanvankelijk verhoogde en langzaam dalende toon die bij passeren tot de werkelijke toonhoogte afneemt en vervolgens daalt naar een verlaagde waarde.
We merken nog op dat wanneer een geluidsbron op de waarnemer toekomt met een snelheid die de geluidssnelheid nadert, de noemer in bovenstaande formule naar 0 gaat. De golffronten hopen zich op: er ontstaat een geluidsbarrière.
Bovenstaande formule kan worden vereenvoudigd als bron of waarnemer stilstaan.
In het geval dat de waarnemer in rust is en de bron beweegt ten opzichte van het medium, geldt voor de waargenomen frequentie :
waarbij positief is genomen als bron en waarnemer elkaar naderen.
Als de golfbron in rust is ten opzichte van het medium en de waarnemer zich beweegt ten opzichte van de bron, geldt voor de waargenomen frequentie :
waarbij positief is als bron en waarnemer elkaar naderen.
Licht en andere elektromagnetische golven
Omdat elektromagnetische golven zoals licht zich weliswaar in een medium kunnen voortplanten (en ook in vacuüm), maar niet door het medium worden voortgeplant, is het dopplereffect voor deze golven anders[3][4]. Licht heeft ten opzichte van de waarnemer altijd dezelfde snelheid, wat ook de snelheid is van de waarnemer ten opzichte van de lichtbron. We beschouwen daarom hier alleen het geval waarin de waarnemer beweegt ten opzichte van de lichtbron of, wat hetzelfde is, de lichtbron beweegt ten opzichte van de waarnemer. Alleen de relatieve snelheid van de twee speelt een rol.
Een lichtbron zendt golven uit met een periode Tb (de tijd tussen twee maxima of tussen twee minima van de golf). Als de bron zich met een snelheid v naar de waarnemer toe beweegt, verandert voor de waarnemer de golflengte, want tijdens elke periode vermindert de afstand met een bedrag vTb . Indien λb de golflengte is bij stilstand, dan is de afstand tussen twee maxima van de golf bij nadering van de bron vTb korter en bij verwijdering vTb langer dan λb. Algemeen kunnen we dus schrijven dat de waarnemer een golflengte λ meet gegeven door
Hier geldt het min-teken voor een nadering, en het plus-teken voor een verwijdering van bron en waarnemer. Met Tb is 1/fb vinden we zo voor de waargenomen golflengte
De snelheid van het licht is onveranderlijk c en dus heeft de lichtgolf voor de waarnemer een frequentie
- zodat
Voor snelheden die klein zijn in vergelijking tot de lichtsnelheid verandert frequentie dus bijna niet. Bij hoge snelheden wordt de frequentie bij een nadering groter (de kleur van het licht verschuift naar blauw) en bij een verwijdering kleiner (verschuiving naar rood).
Indien de lichtgolf zich voortplant in een middenstof met een brekingsindex n dan vervangt men in de bovenstaande formules c door cm met cm=c/n en men bekomt dan zodat
Relativistisch dopplereffect
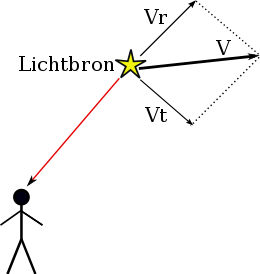
We beschouwen het algemene geval van een lichtbron die niet alleen een radiale snelheidscomponent heeft (beweging volgens de verbindingslijn tussen de waarnemer en de lichtbron) maar ook een transversale (loodrecht op de verbindingslijn). De snelheid v kan dus ontbonden worden in beide componenten, zo dat geldt:
waarin vr en vt de radiale en de transversale snelheidscomponenten voorstellen.
De lichtbron zendt een lichtgolf uit met een golflengte λb en een periode Tb. Tijdens de duur van één periode verplaatst de bron zich in de richting van de waarnemer over een afstand vrTb. Daardoor meet de waarnemer een golflengte
- zoals hierboven reeds vermeld.
Met λw=cTw en λb=cTb kunnen na deling door c schrijven:
Tot zover de klassieke behandeling. In het stelsel van de waarnemer die niet meebeweegt met de lichtbron moeten we rekening houden met de relativistische tijddilatatie. Tb is de duur van een periode in het stelsel van de lichtbron. Voor de waarnemer is Tb uitgerekt tot een waarde (de snelheid in de factor γ is de 'hele' snelheid v, en niet slechts de radiale snelheid Vr, omdat de tijddilatatie niet afhangt van de richting van de beweging t.o.v. de waarnemer. De waarnemer meet dus een tijd Tw:
- met Tw=1/fw en Tb=1/fb vinden we
Indien er alleen een radiale snelheid is (vt=0, vr=v) krijgen we voor een nadering
- en analoog voor een verwijdering
Als dan wordt zodat en krijgen we de formules terug voor het klassieke dopplereffect voor licht.
Voor een middenstof met brekingsindex n krijgen we
Hierin is:
- de lichtsnelheid
- de snelheid van het licht in het betrokken medium
- de brekingsindex, waarbij
- de snelheid waarmee bron en waarnemer elkaar naderen (negatief als zij zich van elkaar verwijderen).
Transversaal dopplereffect
Het relativistische dopplereffect treedt ook op wanneer de radiale snelheid nul is en de bron alleen een snelheid vt loodrecht op de gezichtslijn heeft. In de klassieke voorstelling is er in dat geval geen dopplereffect. Maar wegens de tijddilatatie treedt bij een louter transversale beweging toch een frequentie-verandering op, gegeven door de formule:
Het relativistisch dopplereffect kon in de jaren 1960 experimenteel worden geverifieerd met een absolute fout van 10-5 door de Mössbauer-rotor-experimenten.
Toepassingen
Het dopplereffect wordt algemeen toegepast om snelheden te meten. Hierbij kan alleen de snelheidscomponent van of naar de waarnemer bepaald worden (radiële snelheid). Voor deze component geldt
met de snelheid van de golfbron, en de hoek tussen de snelheidsrichting (vector) en de gezichtlijn van bron naar waarnemer.
Als bewegende gassen licht uitstralen of absorberen, wordt hun spectraallijn beïnvloed door het dopplereffect: de zogenaamde dopplerverbreding van de spectraallijn treedt op.
Sterrenkunde
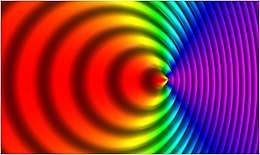
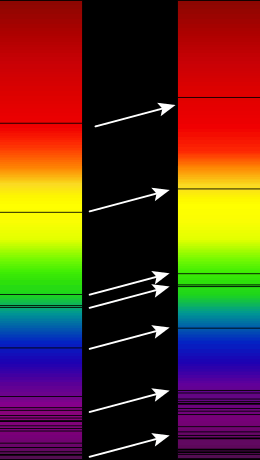
In de astronomie is het door het dopplereffect mogelijk nauwkeurig vast te stellen of een hemellichaam zich naar ons toe of van ons af beweegt. Hiervoor is natuurlijk nodig dat men weet wat de oorspronkelijke golflengte van het licht is, maar dat is eenvoudig, omdat het licht steeds spectraallijnen bevat waarvan de golflengte bekend is. Wanneer een ster zich van de waarnemer af beweegt wordt waargenomen dat de kleur naar het rood verschoven is (zogenoemde roodverschuiving); omgekeerd, wanneer de ster zich naar de waarnemer toe beweegt wordt een kleur- of spectraalverschuiving naar het blauw toe waargenomen.
Voorbeeld
Om de snelheid van een ster te bepalen vertrekt men van de klassieke uitdrukking van het dopplereffect voor licht
- zodat waaruit volgt dat
De ster Vega (α Lyrae), de helderste ster in het sterrenbeeld Lier bevindt zich op een afstand van 25,04 lichtjaar. In haar spectrum vindt men een sterke absortielijn van waterstof (de Hα-lijn) met een golflengte van λw=6562,5 Å (1 Å is gelijk aan 10-10 m). In het laboratorium meet men voor dezelfde absorptielijn een golflengte λb=6562,8 Å. Met behulp van de formule kunnen we nu de radiale snelheid berekenen
- km/s
Het minteken (blauwverschuiving) wijst erop dat deze ster zich naar ons toe beweegt. Aangezien Vr<<c is het wel geoorloofd om de benaderende formule te gebruiken. Noteer ook dat de opgegeven Hα-lijn van Vega een gemiddelde positie van deze absorptielijn is. Immers deze lijn gaat elke zes maanden op en neer tengevolge van de baanbeweging (29,8 km/s) van de aarde om de zon.
Kosmologie
Het is dankzij deze waarnemingen dat men weet dat het heelal uitdijt: de sterrenstelsels vluchten van elkaar weg.
Deze waarnemingen zijn zeer nauwkeurig, ongeacht de afstand tot het hemellichaam. Het is bij grotere afstanden daarentegen vrijwel onmogelijk te constateren of een hemellichaam een beweging uitvoert loodrecht op de kijkrichting, en de astronomische afstandsmeting is ook bijzonder onnauwkeurig.
Het Dopplereffect is niet alleen van toepassing op golven, maar op ieder waargenomen periodiek proces, bijvoorbeeld het om elkaar heen draaien van de componenten van een dubbelster: als de dubbelster met bijvoorbeeld 30 km/s in onze richting komt en een omlooptijd heeft van 100 jaar lijkt die omlooptijd 4 dagen korter.
Verkeer
Door het dopplereffect kan de politie de snelheid van voertuigen meten. Er wordt een radarstraal op het voertuig gericht. Uit de golflengteverschil tussen de uitgezonden en de teruggekaatste straal blijkt de snelheid.
Geneeskunde
In de geneeskunde vindt het akoestische dopplereffect een toepassing bij onderzoek naar de snelheid van het bloed in de aderen, dat met ultrasoon geluid kan worden gemeten.
Militair
Onderzeeboten gebruiken het dopplereffect in passieve en actieve Sonar-systemen. De nabijheidsbuis/nabijheidsontsteking (proximity fuse) die een projectiel bij zijn doel laat ontploffen, werkt ook met het dopplereffect.
Stromingsleer
Om de stroomsnelheid van gassen (wind) en vloeistoffen te meten, worden laserdopplersystemen gebruikt waarbij laserlicht verstrooid wordt aan deeltjes in de stroming. Een voorbeeld is de laserdoppleranemometer voor windmeting.
Radio en radar
In het radiospectrum wordt het dopplereffect gebruikt bij GPS-systemen en in radarsystemen. Dit laatste noemt men dopplerradar. Dit systeem wordt onder meer gebruikt voor het detecteren van neerslag, en in de radar- of lasersnelheidscontrole door de politie.
Externe links
- Dopplereffect op www.natuurkunde.nl
- Animatie Klik in het grijze vierkant, beweeg de muis, laat los. Het machgetal wordt weergegeven.
Bronnen, noten en/of referenties
|
| Zie de categorie Doppler effect van Wikimedia Commons voor mediabestanden over dit onderwerp. |