Perspectivity
In geometry and in its applications to drawing, a perspectivity is the formation of an image in a picture plane of a scene viewed from a fixed point.
Graphics
The science of graphical perspective uses perspectivities to make realistic images in proper proportion. According to Kirsti Andersen, the first author to describe perspectivity was Leon Alberti in his De Pictura (1435).[1] In English, Brook Taylor presented his Linear Perspective in 1715, where he explained "Perspective is the Art of drawing on a Plane the Appearances of any Figures, by the Rules of Geometry".[2] In a second book, New Principles of Linear Perspective (1719), Taylor wrote
- When Lines drawn according to a certain Law from the several Parts of any Figure, cut a Plane, and by that Cutting or Intersection describe a figure on that Plane, that Figure so described is called the Projection of the other Figure. The Lines producing that Projection, taken all together, are called the System of Rays. And when those Rays all pass thro’ one and same Point, they are called the Cone of Rays. And when that Point is consider’d as the Eye of a Spectator, that System of Rays is called the Optic Cone[3]
Projective geometry
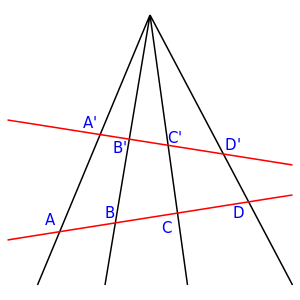
In projective geometry the points of a line are called a projective range, and the set of lines in a plane on a point is called a pencil.
Given two lines and in a plane and a point P of that plane on neither line, the bijective mapping between the points of the range of and the range of determined by the lines of the pencil on P is called a perspectivity (or more precisely, a central perspectivity with center P).[4] A special symbol has been used to show that points X and Y are related by a perspectivity; In this notation, to show that the center of perspectivity is P, write
The existence of a perspectivity means that corresponding points are in perspective. The dual concept, axial perspectivity, is the correspondence between the lines of two pencils determined by a projective range.
Projectivity
The composition of two perspectivities is, in general, not a perspectivity. A perspectivity or a composition of two or more perspectivities is called a projectivity (projective transformation, projective collineation and homography are synonyms).
There are several results concerning projectivities and perspectivities which hold in any pappian projective plane:[5]
Theorem: Any projectivity between two distinct projective ranges can be written as the composition of no more than two perspectivities.
Theorem: Any projectivity from a projective range to itself can be written as the composition of three perspectivities.
Theorem: A projectivity between two distinct projective ranges which fixes a point is a perspectivity.
Higher-dimensional perspectivities
The bijective correspondence between points on two lines in a plane determined by a point of that plane not on either line has higher-dimensional analogues which will also be called perspectivities.
Let Sm and Tm be two distinct m-dimensional projective spaces contained in an n-dimensional projective space Rn. Let Pn−m−1 be an (n − m − 1)-dimensional subspace of Rn with no points in common with either Sm or Tm. For each point X of Sm, the space L spanned by X and Pn-m-1 meets Tm in a point Y = fP(X). This correspondence fP is also called a perspectivity.[6] The central perspectivity described above is the case with n = 2 and m = 1.
Perspective collineations
Let S2 and T2 be two distinct projective planes in a projective 3-space R3. With O and O* being points of R3 in neither plane, use the construction of the last section to project S2 onto T2 by the perspectivity with center O followed by the projection of T2 back onto S2 with the perspectivity with center O*. This composition is a bijective map of the points of S2 onto itself which preserves collinear points and is called a perspective collineation (central collineation in more modern terminology).[7] Let φ be a perspective collineation of S2. Each point of the line of intersection of S2 and T2 will be fixed by φ and this line is called the axis of φ. Let point P be the intersection of line OO* with the plane S2. P is also fixed by φ and every line of S2 that passes through P is stabilized by φ (fixed, but not necessarily pointwise fixed). P is called the center of φ. The restriction of φ to any line of S2 not passing through P is the central perspectivity in S2 with center P between that line and the line which is its image under φ.
Notes

- Kirsti Andersen (2007) The Geometry of an Art, page 1,Springer ISBN 978-0-387-25961-1
- Andersen 1992, p. 75
- Andersen 1992, p. 163
- Coxeter 1969, p. 242
- Fishback 1969, pp. 65–66
- Pedoe 1988, pp. 282–3
- Young 1930, p. 116
References
- Andersen, Kirsti (1992), Brook Taylor's Work on Linear Perspective, Springer, ISBN 0-387-97486-5
- Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0, MR 0123930
- Fishback, W.T. (1969), Projective and Euclidean Geometry, John Wiley & Sons
- Pedoe, Dan (1988), Geometry/A Comprehensive Course, Dover, ISBN 0-486-65812-0
- Young, John Wesley (1930), Projective Geometry, The Carus Mathematical Monographs (#4), Mathematical Association of America
External links
- Christopher Cooper Perspectivities and Projectivities.
- James C. Morehead Jr. (1911) Perspective and Projective Geometries: A Comparison from Rice University.
- John Taylor Projective Geometry from University of Brighton.