Multiplicative cascade

In mathematics, a multiplicative cascade[1][2] is a fractal/multifractal distribution of points produced via an iterative and multiplicative random process.

Model I (left plot):

${\displaystyle \lbrace p_{1},p_{2},p_{3},p_{4}\rbrace =\lbrace 1,1,1,0\rbrace }$

Model II (middle plot):

${\displaystyle \lbrace p_{1},p_{2},p_{3},p_{4}\rbrace =\lbrace 1,0.75,0.75,0.5\rbrace }$

Model III (right plot):

${\displaystyle \lbrace p_{1},p_{2},p_{3},p_{4}\rbrace =\lbrace 1,0.5,0.5,0.25\rbrace }$

The plots above are examples of multiplicative cascade multifractals. To create these distributions there are a few steps to take. Firstly, we must create a lattice of cells which will be our underlying probability density field.

Secondly, an iterative process is followed to create multiple levels of the lattice: at each iteration the cells are split into four equal parts (cells). Each new cell is then assigned a probability randomly from the set ${\displaystyle \lbrace p_{1},p_{2},p_{3},p_{4}\rbrace }$ without replacement, where ${\displaystyle p_{i}\in [0,1]}$. This process is continued to the Nth level. For example, in constructing such a model down to level 8 we produce a 4⁸ array of cells.

Thirdly, the cells are filled as follows: We take the probability of a cell being occupied as the product of the cell's own p_i and those of all its parents (up to level 1). A Monte Carlo rejection scheme is used repeatedly until the desired cell population is obtained, as follows: x and y cell coordinates are chosen randomly, and a random number between 0 and 1 is assigned; the (x, y) cell is then populated depending on whether the assigned number is lesser than (outcome: not populated) or greater or equal to (outcome: populated) the cell's occupation probability.

To produce the plots above we filled the probability density field with 5,000 points in a space of 256 × 256.

An example of the probability density field:

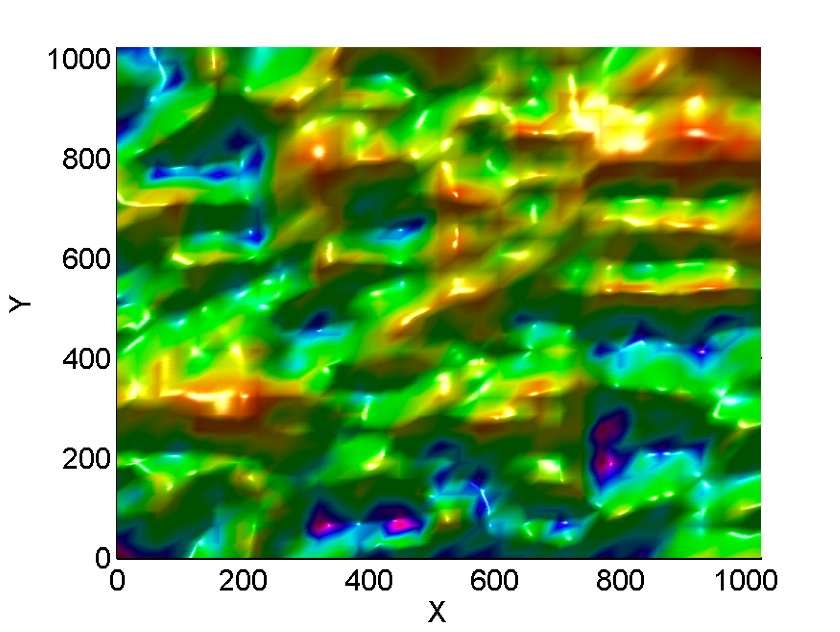
The fractals are generally not scale-invariant and therefore cannot be considered standard fractals. They can however be considered multifractals. The Rényi (generalized) dimensions can be theoretically predicted. It can be shown [3] that as ${\displaystyle N\rightarrow \infty }$,

${\displaystyle D_{q}={\frac {\log _{2}\left(f_{1}^{q}+f_{2}^{q}+f_{3}^{q}+f_{4}^{q}\right)}{1-q}},}$

where N is the level of the grid refinement and,

${\displaystyle f_{i}={\frac {p_{i}}{\sum _{i}p_{i}}}.}$