Maxwell construction
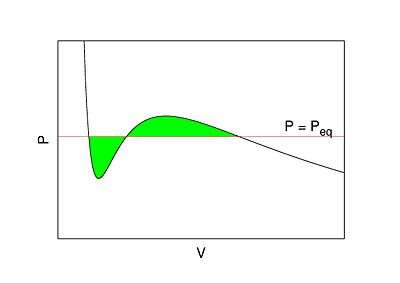
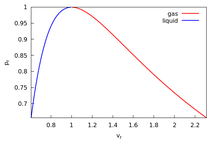
In thermodynamic equilibrium, a necessary condition for stability is that pressure does not increase with volume . This basic consistency requirement—and similar ones for other conjugate pairs of variables—are sometimes violated in analytic models for first order phase transitions. The most famous case is the Van der Waals equation for real gases, see Fig. 1 where a typical isotherm is drawn (black curve). The Maxwell construction is a way of correcting this deficiency. The decreasing right hand part of the curve in Fig. 1 describes a diluted gas, while its left part describes a liquid. The intermediate (rising) part of the curve in Fig. 1 would be correct, if these two parts were to be joined smoothly—meaning in particular that the system would remain also in this region spatially uniform with a well defined density. But this is not what happens. If the volume of a vessel containing a fixed amount of liquid is expanded at constant temperature, there comes a point where some of the liquid boils and the system consists of two well separated phases. While this two-phase coexistence holds as the volume continues to increase, the pressure remains constant. It decreases again, after all liquid is evaporated and the gas expands. Thus the sinusoidal part of the isotherm is replaced by a horizontal line (red line in Fig. 1). According to the Maxwell construction (or "equal area rule"), the height of the horizontal line is such that the two green areas in Fig. 1 are equal.
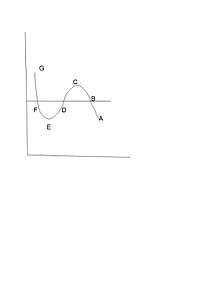
The direct quote from James Clerk Maxwell which became the Maxwell construction: “Now let us suppose the medium to pass from B to F along the hypothetical curve BCDEF in a state always homogeneous, and to return along the straight line path FB in the form of a mixture of liquid and vapour. Since the temperature has been constant throughout, no heat can have been transformed into work. Now the heat transformed into work is represented by the excess of the area FDE over BCD. hence the condition which determine the maximum pressure of the vapour at given temperature is that the line BF cuts off equal areas from the curve above and below.”
Solving the cubic to obtain vapor pressures
The van der Waals gas equation (using reduced variables) can be expanded [1] to
which is of the form
To solve this Cubic function one defines several precursor terms :
and
so that the following become defined
and
The first root’s precursor form is:
leading to
and
and finally
These last four equations depend on two variables, the temperature which is chosen when one determines which isotherm one is working on, and the pressure. One starts with an arbitrary (but reasonable) chosen value and adjusts its values as one solves the equation (below) ultimately obtaining or through the Maxwell construction (see below) at that temperature. With these two variables in hand, one can re-substitute the pressure value obtained into the root equations (above) to obtain the three roots.
The Maxwell construction requires solution of the equation (obtained by making the areas under the two loops equal and opposite in value from each other):
with a fixed reduced temperature and the solution depending then on the chosen variable reduced pressure, which becomes the reduced vapor pressure. Unfortunately, this equation can not be solved analytically, and requires numerical evaluation. The subscripts in this equation are and have been changed to make clear which two roots of the cubic are to be employed; these roots themselves depend on the equations which precede them (above), and contain the reduced pressure and temperature which are treated as above.
An alternative approach without obtaining roots
By equating the pressures corresponding to the two volumes where there is a discontinuity in the p-v isotherm, one obtains an expression for the temperature independent of pressure, i.e.,
which allows elimination of the temperature from the prior equation. Its solution is complicated, but finally becomes
and
where
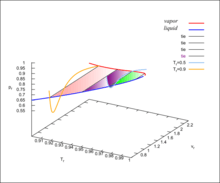
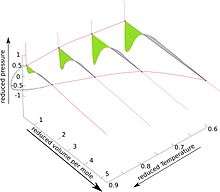
The pseudo-3D diagram for the van der Waals fluid is shown in the accompanying Figure. For details see lectures from University of Connecticut, articles 88, 93, 95 and especially 96.[2]
The Maxwell construction is rarely derived from the condition that the Gibbs free energies of the gas and the liquid must be equal when they coexist. However, it can be shown that this condition is fulfilled. Essentially the same applies to any other thermodynamic system, where and are replaced by a different pair of conjugate variables, e.g. magnetic field and magnetization or chemical potential and number of particles.
Common tangent construction and lever rule
The Maxwell construction is related to the common tangent construction[3][4] and the lever rule[5].
References
- David, Carl W., "The van der Waals Equation as a cubic" (2015). Chemistry Education Materials. Paper 88. http://digitalcommons.uconn.edu/chem_educ/88
- Avoiding the cubic equation in finding the van der Waals Fluid's vapor pressures from University of Connecticut.
- Wales, David; Wales (2003). Energy Landscapes: Applications to Clusters, Biomolecules and Glasses. Cambridge University Press. p. 444. ISBN 9780521814157.
- "First order phase transitions and the dynamics of spinodal decomposition". www.mhkoepf.de. Retrieved 2019-11-12.
- Kondepudi, Dilip; Prigogine, Ilya (2014-12-31). Modern Thermodynamics: From Heat Engines to Dissipative Structures. John Wiley & Sons. ISBN 9781118371817.
- Maxwell, J. C. (1875). "On the Dynamical Evidence of the Molecular Constitution of Bodies". Nature. 11: 357–359. Bibcode:1875Natur..11..357C. doi:10.1038/011357a0.
- Reichl, L. E. (2009). A Modern Course in Statistical Physics (3rd ed.). New York, NY USA: Wiley-VCH. ISBN 9783527407828.