Kobon triangle problem
The Kobon triangle problem is an unsolved problem in combinatorial geometry first stated by Kobon Fujimura. The problem asks for the largest number N(k) of nonoverlapping triangles whose sides lie on an arrangement of k lines. Variations of the problem consider the projective plane rather than the Euclidean plane, and require that the triangles not be crossed by any other lines of the arrangement.[1]
| Unsolved problem in mathematics: How many non-overlapping triangles can be formed in an arrangement of lines? (more unsolved problems in mathematics) |
Saburo Tamura proved that the largest integer not exceeding k(k − 2)/3 provides an upper bound on the maximal number of nonoverlapping triangles realizable by k lines.[2] In 2007, a tighter upper bound was found by Johannes Bader and Gilles Clément, by proving that Tamura's upper bound couldn't be reached for any k congruent to 0 or 2 (mod 6).[3] The maximum number of triangles is therefore at most one less than Tamura's bound in these cases. Perfect solutions (Kobon triangle solutions yielding the maximum number of triangles) are known for k = 3, 4, 5, 6, 7, 8, 9, 13, 15 and 17.[4] For k = 10, 11 and 12, the best solutions known reach a number of triangles one less than the upper bound.
As proved by G. Clément and J. Bader,[3] the solutions for k > 2 are bounded above by
- , when k=={3, 5} (mod 6);
- , when k=={0, 2} (mod 6);
- , when k=={1, 4} (mod 6).
(The floor function is handled by noting that the expression k(k − 2) is a multiple of 3 in the first case and 2 more than a multiple of 3 in the third case; Clément and Bader only improved the bound on the middle case.)
Given a perfect solution with k0>3 lines, other Kobon triangle solution numbers can be found for all ki-values where
by using the procedure by D. Forge and J. L. Ramirez Alfonsin.[1][5] For example, the solution for k0 = 5 leads to the maximal number of nonoverlapping triangles for k = 5,9,17,33,65,...
| k | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | OEIS |
| Tamura's upper bound on N(k) | 1 | 2 | 5 | 8 | 11 | 16 | 21 | 26 | 33 | 40 | 47 | 56 | 65 | 74 | 85 | 96 | 107 | 120 | 133 | A032765 |
| Clément and Bader's upper bound | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 26 | 33 | 39 | 47 | 55 | 65 | 74 | 85 | 95 | 107 | 119 | 133 | - |
| best known solution | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 25 | 32 | 38 | 47 | 53 | 65 | 72 | 85 | 93 | 104 | 115 | 130 | A006066 |
Examples
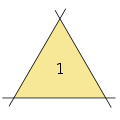 3 straight lines result in one triangle
3 straight lines result in one triangle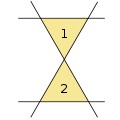 4 straight lines
4 straight lines 5 straight lines
5 straight lines 6 straight lines
6 straight lines 7 straight lines
7 straight lines
See also
- Roberts' triangle theorem
References
- Forge, D.; Ramírez Alfonsín, J. L. (1998), "Straight line arrangements in the real projective plane", Discrete and Computational Geometry, 20 (2): 155–161, doi:10.1007/PL00009373.
- Weisstein, Eric W. "Kobon Triangle". MathWorld.
- "G. Clément and J. Bader. Tighter Upper Bound for the Number of Kobon Triangles. Draft Version, 2007" (PDF). Archived from the original (PDF) on 2017-11-11. Retrieved 2008-03-03.
- Ed Pegg Jr. on Math Games
- "Matlab code illustrating the procedure of D. Forge and J. L. Ramirez Alfonsin", Retrieved on 9 May 2012.
External links
- Johannes Bader, "Kobon Triangles"