K-stability

Generic fibres of a test configuration are all isomorphic to the variety X, whereas the central fibre may be distinct, and even singular.

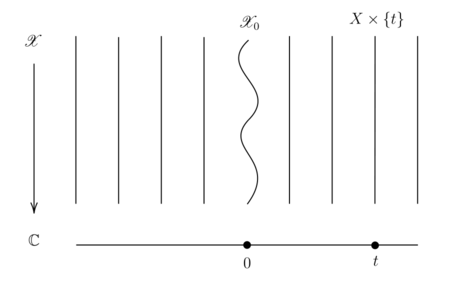
A test configuration for a polarised variety ${\displaystyle (X,L)}$ is a pair ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ where ${\displaystyle {\mathcal {X}}}$ is a scheme with a flat morphism ${\displaystyle \pi :{\mathcal {X}}\to \mathbb {C} }$ and ${\displaystyle {\mathcal {L}}}$ is a relatively ample line bundle for the morphism ${\displaystyle \pi }$, such that:

1. For every ${\displaystyle t\in \mathbb {C} }$, the Hilbert polynomial of the fibre ${\displaystyle ({\mathcal {X}}_{t},{\mathcal {L}}_{t})}$ is equal to the Hilbert polynomial ${\displaystyle {\mathcal {P}}(k)}$ of ${\displaystyle (X,L)}$. This is a consequence of the flatness of ${\displaystyle \pi }$.
2. There is an action of ${\displaystyle \mathbb {C} ^{*}}$ on the family ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ covering the standard action of ${\displaystyle \mathbb {C} ^{*}}$ on ${\displaystyle \mathbb {C} }$.
3. For any (and hence every) ${\displaystyle t\in \mathbb {C} ^{*}}$, ${\displaystyle ({\mathcal {X}}_{t},{\mathcal {L}}_{t})\cong (X,L)}$ as polarised varieties. In particular away from ${\displaystyle 0\in \mathbb {C} }$, the family is trivial: ${\displaystyle ({\mathcal {X}}_{t\neq 0},{\mathcal {L}}_{t\neq 0})\cong (X\times \mathbb {C} ^{*},\operatorname {pr} _{1}^{*}L)}$ where ${\displaystyle \operatorname {pr} _{1}:X\times \mathbb {C} ^{*}\to X}$ is projection onto the first factor.

We say that a test configuration ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ is a product configuration if ${\displaystyle {\mathcal {X}}\cong X\times \mathbb {C} }$, and a trivial configuration if the ${\displaystyle \mathbb {C} ^{*}}$ action on ${\displaystyle {\mathcal {X}}\cong X\times \mathbb {C} }$ is trivial on the first factor.

To define a notion of stability analogous to the Hilbert-Mumford criterion, one needs a concept of weight${\displaystyle \mu ({\mathcal {X}},{\mathcal {L}})}$ on the fibre over ${\displaystyle 0}$ of a test configuration ${\displaystyle ({\mathcal {X}},{\mathcal {L}})\to \mathbb {C} }$ for a polarised variety ${\displaystyle (X,L)}$. By definition this family comes equipped with an action of ${\displaystyle \mathbb {C} ^{*}}$ covering the action on the base, and so the fibre of the test configuration over ${\displaystyle 0\in \mathbb {C} }$ is fixed. That is, we have an action of ${\displaystyle \mathbb {C} ^{*}}$ on the central fibre ${\displaystyle ({\mathcal {X}}_{0},{\mathcal {L}}_{0})}$. In general this central fibre is not smooth, or even a variety. There are several ways to define the weight on the central fiber. The first definition was given by using Ding-Tian's version of generalized Futaki invariant.[18]This definition is differential geometric and is directly related to the existence problems in Kähler geometry. Algebraic definitions were given by using Donaldson-Futaki invariants and CM-weights defined by intersection formula.

By definition an action of ${\displaystyle \mathbb {C} ^{*}}$ on a polarised scheme comes with an action of ${\displaystyle \mathbb {C} ^{*}}$ on the ample line bundle ${\displaystyle {\mathcal {L}}_{0}}$, and therefore induces an action on the vector spaces ${\displaystyle H^{0}({\mathcal {X}}_{0},{\mathcal {L}}_{0}^{k})}$ for all integers ${\displaystyle k\geq 0}$. An action of ${\displaystyle \mathbb {C} ^{*}}$ on a complex vector space ${\displaystyle V}$ induces a direct sum decomposition ${\displaystyle V=V_{1}\oplus \cdots \oplus V_{n}}$ into weight spaces, where each ${\displaystyle V_{i}}$ is a one dimensional subspace of ${\displaystyle V}$, and the action of ${\displaystyle \mathbb {C} ^{*}}$ when restricted to ${\displaystyle V_{i}}$ has a weight ${\displaystyle w_{i}}$. Define the total weight of the action to be the integer ${\displaystyle w=w_{1}+\cdots +w_{n}}$. This is the same as the weight of the induced action of ${\displaystyle \mathbb {C} ^{*}}$ on the one dimensional vector space ${\displaystyle \bigwedge ^{n}V}$ where ${\displaystyle n=\dim V}$.

Define the weight function of the test configuration ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ to be the function ${\displaystyle w(k)}$ where ${\displaystyle w(k)}$ is the total weight of the ${\displaystyle \mathbb {C} ^{*}}$ action on the vector space ${\displaystyle H^{0}({\mathcal {X}}_{0},{\mathcal {L}}_{0}^{k})}$ for each non-negative integer ${\displaystyle k\geq 0}$. Whilst the function ${\displaystyle w(k)}$ is not a polynomial in general, it becomes a polynomial of degree ${\displaystyle n+1}$ for all ${\displaystyle k>k_{0}\gg 0}$ for some fixed integer ${\displaystyle k_{0}}$, where ${\displaystyle n=\dim X}$. This can be seen using an equivariant Riemann-Roch theorem. Recall that the Hilbert polynomial ${\displaystyle {\mathcal {P}}(k)}$ satisfies the equality ${\displaystyle {\mathcal {P}}(k)=\dim H^{0}(X,L^{k})=\dim H^{0}({\mathcal {X}}_{0},{\mathcal {L}}_{0}^{k})}$ for all ${\displaystyle k>k_{1}\gg 0}$ for some fixed integer ${\displaystyle k_{1}}$, and is a polynomial of degree ${\displaystyle n}$. For such ${\displaystyle k\gg 0}$, let us write

${\displaystyle {\mathcal {P}}(k)=a_{0}k^{n}+a_{1}k^{n-1}+O(k^{n-2}),\quad w(k)=b_{0}k^{n+1}+b_{1}k^{n}+O(k^{n-1})}$.

The Donaldson-Futaki invariant of the test configuration ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ is the rational number

${\displaystyle \operatorname {DF} ({\mathcal {X}},{\mathcal {L}})={\frac {b_{0}a_{1}-b_{1}a_{0}}{a_{0}^{2}}}}$.

In particular ${\displaystyle \operatorname {DF} ({\mathcal {X}},{\mathcal {L}})=-f_{1}}$ where ${\displaystyle f_{1}}$ is the first order term in the expansion

${\displaystyle {\frac {w(k)}{k{\mathcal {P}}(k)}}=f_{0}+f_{1}k^{-1}+O(k^{-2})}$.

The Donaldson-Futaki invariant does not change if ${\displaystyle L}$ is replaced by a positive power ${\displaystyle L^{r}}$, and so in the literature K-stability is often discussed using ${\displaystyle \mathbb {Q} }$-line bundles.

It is possible to describe the Donaldson-Futaki invariant in terms of intersection theory, and this was the approach taken by Tian in defining the CM-weight[19]. Any test configuration ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ admits a natural compactification ${\displaystyle ({\bar {\mathcal {X}}},{\bar {\mathcal {L}}})}$ over ${\displaystyle \mathbb {P} ^{1}}$ (e.g.,see [20][21]), then the CM-weight is defined by

${\displaystyle CM({\mathcal {X}},{\mathcal {L}})={\frac {1}{2(n+1)\cdot L^{n}}}\left(\mu \cdot n{({\bar {\mathcal {L}}})}^{n+1}+(n+1){K}_{{\bar {\mathcal {X}}}/{\mathbb {P} }^{1}}\cdot {({\bar {\mathcal {L}}})}^{n}\right)}$

where ${\displaystyle \mu ={\frac {L^{n-1}\cdot K_{X}}{L^{n}}}}$. This definition by intersection formula is now often used in algebraic geometry.

It is known that ${\displaystyle \operatorname {DF} ({\mathcal {X}},{\mathcal {L}})}$ coincides with ${\displaystyle \operatorname {CM} ({\mathcal {X}},{\mathcal {L}})}$, so we can take the weight ${\displaystyle \mu ({\mathcal {X}},{\mathcal {L}})}$ to be either ${\displaystyle \operatorname {DF} ({\mathcal {X}},{\mathcal {L}})}$ or ${\displaystyle \operatorname {CM} ({\mathcal {X}},{\mathcal {L}})}$. The weight ${\displaystyle \mu ({\mathcal {X}},{\mathcal {L}})}$ can be also expressed in terms of theChow form and hyperdiscriminant.[22] In the case of Fano manifolds, there is an interpretation of the weight in terms of new ${\displaystyle \beta }$-invariant on valuations found by Chi Li[23] and Kento Fujita[24].

In order to define K-stability, we need to first exclude certain test configurations. Initially it was presumed one should just ignore trivial test configurations as defined above, whose Donaldson-Futaki invariant always vanishes, but it was observed by Li and Xu that more care is needed in the definition.[25][26] One elegant way of defining K-stability is given by Székelyhidi using the norm of a test configuration, which we first describe.[27]

For a test configuration ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$, define the norm as follows. Let ${\displaystyle A_{k}}$ be the infinitesimal generator of the ${\displaystyle \mathbb {C} ^{*}}$ action on the vector space ${\displaystyle H^{0}(X,L^{k})}$. Then ${\displaystyle \operatorname {Tr} (A_{k})=w(k)}$. Similarly to the polynomials ${\displaystyle w(k)}$ and ${\displaystyle {\mathcal {P}}(k)}$, the function ${\displaystyle \operatorname {Tr} (A_{k}^{2})}$ is a polynomial for large enough integers ${\displaystyle k}$, in this case of degree ${\displaystyle n+2}$. Let us write its expansion as

${\displaystyle \operatorname {Tr} (A_{k}^{2})=c_{0}k^{n+2}+O(k^{n+1}).}$

The norm of a test configuration is defined by the expression

${\displaystyle \|({\mathcal {X}},{\mathcal {L}})\|^{2}=c_{0}-{\frac {b_{0}^{2}}{a_{0}}}.}$

According to the analogy with the Hilbert-Mumford criterion, once one has a notion of deformation (test configuration) and weight on the central fibre (Donaldson-Futaki invariant), one can define a stability condition, called K-stability.

Let ${\displaystyle (X,L)}$ be a polarised algebraic variety. We say that ${\displaystyle (X,L)}$ is:

• K-semistable if ${\displaystyle \operatorname {\mu } ({\mathcal {X}},{\mathcal {L}})\geq 0}$ for all test configurations ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ for ${\displaystyle (X,L)}$.
• K-stable if ${\displaystyle \operatorname {\mu } ({\mathcal {X}},{\mathcal {L}})\geq 0}$ for all test configurations ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ for ${\displaystyle (X,L)}$, and additionally ${\displaystyle \operatorname {\mu } ({\mathcal {X}},{\mathcal {L}})>0}$ whenever ${\displaystyle \|({\mathcal {X}},{\mathcal {L}})\|>0}$.
• K-polystable if ${\displaystyle (X,L)}$ is K-semistable, and additionally whenever ${\displaystyle \operatorname {\mu } ({\mathcal {X}},{\mathcal {L}})=0}$, the test configuration ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ is a product configuration.
• K-unstable if it is not K-semistable.

It has been known since the original work of Deligne and Mumford that smooth algebraic curves are asymptotically stable in the sense of geometric invariant theory, and in particular that they are K-stable.[37] In this setting, the Yau-Tian-Donaldson conjecture is equivalent to the uniformization theorem. Namely, every smooth curve admits a Kähler-Einstein metric of constant scalar curvature either ${\displaystyle +1}$ in the case of the projective line ${\displaystyle \mathbb {CP} ^{1}}$, ${\displaystyle 0}$ in the case of elliptic curves, or ${\displaystyle -1}$ in the case of compact Riemann surfaces of genus ${\displaystyle g>1}$.

K-stability was originally introduced by Donaldson in the context of toric varieties.[38] In the toric setting many of the complicated definitions of K-stability simplify to be given by data on the moment polytope ${\displaystyle P}$ of the polarised toric variety ${\displaystyle (X_{P},L_{P})}$. First it is known that to test K-stability, it is enough to consider toric test configurations, where the total space of the test configuration is also a toric variety. Any such toric test configuration can be elegantly described by a convex function on the moment polytope, and Donaldson originally defined K-stability for such convex functions. If a toric test configuration ${\displaystyle ({\mathcal {X}},{\mathcal {L}})}$ for ${\displaystyle (X_{P},L_{P})}$ is given by a convex function ${\displaystyle f}$ on ${\displaystyle P}$, then the Donaldson-Futaki invariant can be written as

${\displaystyle \operatorname {DF} ({\mathcal {X}},{\mathcal {L}})={\frac {1}{2}}{\mathcal {L}}(f)={\frac {1}{2}}\left(\int _{\partial P}f\,d\sigma -a\int _{P}f\,d\mu \right)}$,

where ${\displaystyle d\mu }$ is the Lebesgue measure on ${\displaystyle P}$, ${\displaystyle d\sigma }$ is the canonical measure on the boundary of ${\displaystyle P}$ arising from its description as a moment polytope (if an edge of ${\displaystyle P}$ is given by a linear inequality ${\displaystyle h(x)\leq a}$ for some affine linear functional h on ${\displaystyle \mathbb {R} ^{n}}$ with integer coefficients, then ${\displaystyle d\mu =\pm dh\wedge d\sigma }$), and ${\displaystyle a=\operatorname {Vol} (\partial P,d\sigma )/\operatorname {Vol} (P,d\mu )}$. Additionally the norm of the test configuration can be given by

${\displaystyle \|({\mathcal {X}},{\mathcal {L}})\|=\|f-{\bar {f}}\|_{L^{2}}}$,

where ${\displaystyle {\bar {f}}}$ is the average of ${\displaystyle f}$ on ${\displaystyle P}$ with respect to ${\displaystyle d\mu }$.

It was shown by Donaldson that for toric surfaces, it suffices to test convex functions of a particularly simple form. We say a convex function on ${\displaystyle P}$ is piecewise-linear if it can be written as a maximum ${\displaystyle f=\max(h_{1},\dots ,h_{n})}$ for some affine linear functionals ${\displaystyle h_{1},\dots ,h_{n}}$. Notice that by the definition of the constant ${\displaystyle a}$, the Donaldson-Futaki invariant ${\displaystyle {\mathcal {L}}(f)}$ is invariant under the addition of an affine linear functional, so we may always take one of the ${\displaystyle h_{i}}$ to be the constant function ${\displaystyle 0}$. We say a convex function is simple piecewise-linear if it is a maximum of two functions, and so is given by ${\displaystyle f=\max(0,h)}$ for some affine linear function ${\displaystyle h}$, and simple rational piecewise-linear if ${\displaystyle h}$ has rational cofficients. Donaldson showed that for toric surfaces it is enough to test K-stability only on simple rational piecewise-linear functions. Such a result is powerful in so far as it is possible to readily compute the Donaldson-Futaki invariants of such simple test configurations, and therefore computationally determine when a given toric surface is K-stable.

An example of a K-unstable manifold is given by the toric surface ${\displaystyle \mathbb {F} _{1}=\operatorname {Bl} _{0}\mathbb {CP} ^{2}}$, the first Hirzebruch surface, which is the blow up of the complex projective plane at a point, with respect to the polarisation given by ${\displaystyle L={\frac {1}{2}}(\pi ^{*}{\mathcal {O}}(2)-E)}$, where ${\displaystyle \pi :\mathbb {F} _{1}\to \mathbb {CP} ^{2}}$ is the blow up and ${\displaystyle E}$ the exceptional divisor.

The moment polytope of the first Hirzebruch surface.

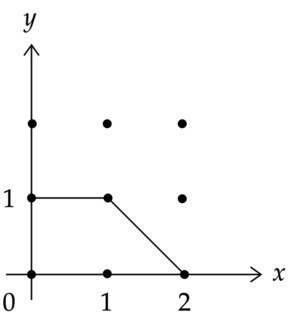
The measure ${\displaystyle d\sigma }$ on the horizontal and vertical boundary faces of the polytope are just ${\displaystyle dx}$ and ${\displaystyle dy}$. On the diagonal face ${\displaystyle x+y=2}$ the measure is given by ${\displaystyle (dx-dy)/2}$. Consider the convex function ${\displaystyle f(x,y)=x+y}$ on this polytope. Then

${\displaystyle \int _{P}f\,d\mu ={\frac {11}{6}},\qquad \int _{\partial P}f\,d\sigma =6}$,

and

${\displaystyle \operatorname {Vol} (P,d\mu )={\frac {3}{2}},\qquad \operatorname {Vol} (\partial P,d\sigma )=5}$.

Thus

${\displaystyle {\mathcal {L}}(f)=6-{\frac {55}{9}}=-{\frac {1}{9}}<0}$,

and so the first Hirzebruch surface ${\displaystyle \mathbb {F} _{1}}$ is K-unstable.

K-stability arises from an analogy with the Hilbert-Mumford criterion for finite-dimensional geometric invariant theory. It is possible to use geometric invariant theory directly to obtain other notions of stability for varieties that are closely related to K-stability.

Take a polarised variety ${\displaystyle (X,L)}$ with Hilbert polynomial ${\displaystyle {\mathcal {P}}}$, and fix an ${\displaystyle r>0}$ such that ${\displaystyle L^{r}}$ is very ample with vanishing higher cohomology. The pair ${\displaystyle (X,L^{r})}$ can then be identified with a point in the Hilbert scheme of subschemes of ${\displaystyle \mathbb {P} ^{{\mathcal {P}}(r)-1}}$ with Hilbert polynomial ${\displaystyle {\mathcal {P}}'(K)={\mathcal {P}}(Kr)}$.

This Hilbert scheme can be embedded into projective space as a subscheme of a Grassmannian (which is projective via the Plücker embedding). The general linear group ${\displaystyle \operatorname {GL} ({\mathcal {P}}(r),\mathbb {C} )}$ acts on this Hilbert scheme, and two points in the Hilbert scheme are equivalent if and only if the corresponding polarised varieties are isomorphic. Thus one can use geometric invariant theory for this group action to give a notion of stability. This construction depends on a choice of ${\displaystyle r>0}$, so one says a polarised variety is asymptotically Hilbert stable if it is stable with respect to this embedding for all ${\displaystyle r>r_{0}\gg 0}$ sufficiently large, for some fixed ${\displaystyle r_{0}}$.

There is another projective embedding of the Hilbert scheme called the Chow embedding, which provides a different linearisation of the Hilbert scheme and therefore a different stability condition. One can similarly therefore define asymptotic Chow stability. Explicitly the Chow weight for a fixed ${\displaystyle r>0}$ can be computed as

${\displaystyle \operatorname {Chow} _{r}({\mathcal {X}},{\mathcal {L}})={\frac {rb_{0}}{a_{0}}}-{\frac {w(r)}{{\mathcal {P}}(r)}}}$

for ${\displaystyle r}$ sufficiently large.[39] Unlike the Donaldson-Futaki invariant, the Chow weight changes if the line bundle ${\displaystyle L}$ is replaced by some power ${\displaystyle L^{k}}$. However, from the expression

${\displaystyle \operatorname {Chow} _{rk}({\mathcal {X}},{\mathcal {L^{k}}})={\frac {krb_{0}}{a_{0}}}-{\frac {w(kr)}{{\mathcal {P}}(kr)}}}$

one observes that

${\displaystyle \operatorname {DF} ({\mathcal {X}},{\mathcal {L}})=\lim _{k\to \infty }\operatorname {Chow} _{rk}({\mathcal {X}},{\mathcal {L^{k}}})}$,

and so K-stability is in some sense the limit of Chow stability as the dimension of the projective space ${\displaystyle X}$ is embedded in approaches infinity.

One may similarly define asymptotic Chow semistability and asymptotic Hilbert semistability, and the various notions of stability are related as follows:

Asymptotically Chow stable ${\displaystyle \implies }$ Asymptotically Hilbert stable ${\displaystyle \implies }$ Asymptotically Hilbert semistable ${\displaystyle \implies }$ Asymptotically Chow semistable ${\displaystyle \implies }$ K-semistable

It is however not know whether K-stability implies asymptotic Chow stability.[40]

It was originally predicted by Yau that the correct notion of stability for varieties should be analogous to slope stability for vector bundles. Julius Ross and Richard Thomas developed a theory of slope stability for varieties, known as slope K-stability. It was shown by Ross and Thomas that any test configuration is essentially obtained by blowing up the variety ${\displaystyle X\times \mathbb {C} }$ along a sequence of ${\displaystyle \mathbb {C} ^{*}}$ invariant ideals, supported on the central fibre.[41] This result is essentially due to David Mumford.[42] Explicitly, every test configuration is dominated by a blow up of ${\displaystyle X\times \mathbb {C} }$ along an ideal of the form

${\displaystyle I=I_{0}+tI_{1}+t^{2}I_{2}+\cdots +t^{r-1}I_{r-1}+(t^{r})\subset {\mathcal {O}}_{X}\otimes \mathbb {C} [t],}$

where ${\displaystyle t}$ is the coordinate on ${\displaystyle \mathbb {C} }$. By taking the support of the ideals this corresponds to blowing up along a flag of subschemes

${\displaystyle Z_{r-1}\subset \cdots \subset Z_{2}\subset Z_{1}\subset Z_{0}\subset X}$

inside the copy ${\displaystyle X\times \{0\}}$ of ${\displaystyle X}$. One obtains this decomposition essentially by taking the weight space decomposition of the invariant ideal ${\displaystyle I}$ under the ${\displaystyle \mathbb {C} ^{*}}$ action.

In the special case where this flag of subschemes is of length one, the Donaldson-Futaki invariant can be easily computed and one arrives at slope K-stability. Given a subscheme ${\displaystyle Z\subset X}$ defined by an ideal sheaf ${\displaystyle I_{Z}}$, the test configuration is given by

${\displaystyle {\mathcal {X}}=\operatorname {Bl} _{Z\times \{0\}}(X\times \mathbb {C} )}$,

which is the deformation to the normal cone of the embedding ${\displaystyle Z\hookrightarrow X}$.

If the variety ${\displaystyle X}$ has Hilbert polynomial ${\displaystyle {\mathcal {P}}(k)=a_{0}k^{n}+a_{1}k^{n-1}+O(k^{n-2})}$, define the slope of ${\displaystyle X}$ to be

${\displaystyle \mu (X)={\frac {a_{1}}{a_{0}}}}$.

To define the slope of the subscheme ${\displaystyle Z}$, consider the Hilbert-Samuel polynomial of the subscheme ${\displaystyle Z}$,

${\displaystyle \chi (L^{r}\otimes I_{Z}^{xr})=a_{0}(x)r^{n}+a_{1}(x)r^{n-1}+O(r^{n-2})}$,

for ${\displaystyle r\gg 0}$ and ${\displaystyle x}$ a rational number such that ${\displaystyle xr\in \mathbb {N} }$. The coefficients ${\displaystyle a_{i}(x)}$ are polynomials in ${\displaystyle x}$ of degree ${\displaystyle n-i}$, and the K-slope of ${\displaystyle I_{Z}}$ with respect to ${\displaystyle c}$ is defined by

${\displaystyle \mu _{c}(I_{Z})={\frac {\int _{0}^{c}(a_{1}(x)+{\frac {a_{0}'(x)}{2}})\,dx}{\int _{0}^{c}a_{0}(x)\,dx}}.}$

This definition makes sense for any choice of real number ${\displaystyle c\in (0,\epsilon (Z)]}$ where ${\displaystyle \epsilon (Z)}$ is the Seshadri constant of ${\displaystyle Z}$. Notice that taking ${\displaystyle Z=\emptyset }$ we recover the slope of ${\displaystyle X}$. The pair ${\displaystyle (X,L)}$ is slope K-semistable if for all proper subschemes ${\displaystyle Z\subset X}$, ${\displaystyle \mu _{c}(I_{Z})\leq \mu (X)}$ for all ${\displaystyle c\in (0,\epsilon (Z)]}$ (one can also define slope K-stability and slope K-polystability by requiring this inequality to be strict, with some extra technical conditions).

It was shown by Ross and Thomas that K-semistability implies slope K-semistability.[43] However, unlike in the case of vector bundles, it is not the case that slope K-stability implies K-stability. In the case of vector bundles it is enough to consider only single subsheaves, but for varieties it is necessary to consider flags of length greater than one also. Despite this, slope K-stability can still be used to identify K-unstable varieties, and therefore by the results of Stoppa, give obstructions to the existence of cscK metrics. For example, Ross and Thomas use slope K-stability to show that the projectivisation of an unstable vector bundle over a K-stable base is K-unstable, and so does not admit a cscK metric. This is a converse to results of Hong, which show that the projectivisation of a stable bundle over a base admitting a cscK metric, also admits a cscK metric, and is therefore K-stable.[44]

Work of Apostolov-Calderbank-Gauduchon-Tønnesen-Friedman shows the existence of a manifold which does not admit any extremal metric, but does not appear to be destabilised by any test configuration.[45] This suggests that the definition of K-stability as given here may not be precise enough to imply the Yau-Tian-Donaldson conjecture in general. However, this example is destabilised by a limit of test configurations. This was made precise by Székelyhidi, who introduced filtration K-stability.[46][47] A filtration here is a filtration of the coordinate ring

${\displaystyle R=\bigoplus _{k\geq 0}H^{0}(X,L^{k})}$

of the polarised variety ${\displaystyle (X,L)}$. The filtrations considered must be compatible with the grading on the coordinate ring in the following sense: A filtation ${\displaystyle \chi }$ of ${\displaystyle R}$ is a chain of finite-dimensional subspaces

${\displaystyle \mathbb {C} =F_{0}R\subset F_{1}R\subset F_{2}R\subset \dots \subset R}$

such that the following conditions hold:

1. The filtration is multiplicative. That is, ${\displaystyle (F_{i}R)(F_{j}R)\subset F_{i+j}R}$ for all ${\displaystyle i,j\geq 0}$.
2. The filtration is compatible with the grading on ${\displaystyle R}$ coming from the graded pieces ${\displaystyle R_{k}=H^{0}(X,L^{k})}$. That is, if ${\displaystyle f\in F_{i}R}$, then each homogenous piece of ${\displaystyle f}$ is in ${\displaystyle F_{i}R}$.
3. The filtration exhausts ${\displaystyle R}$. That is, we have ${\displaystyle \bigcup _{i\geq 0}F_{i}R=R}$.

Given a filtration ${\displaystyle \chi }$, its Rees algebra is defined by

${\displaystyle \operatorname {Rees} (\chi )=\bigoplus _{i\geq 0}(F_{i}R)t^{i}\subset R[t].}$

We say that a filtration is finitely generated if its Rees algebra is finitely generated. It was proven by David Witt Nyström that a filtration is finitely generated if and only if it arises from a test configuration, and by Székelyhidi that any filtration is a limit of finitely generated filtrations.[48] Combining these results Székelyhidi observed that the example of Apostolov-Calderbank-Gauduchon-Tønnesen-Friedman would not violate the Yau-Tian-Donaldson conjecture if K-stability was replaced by filtration K-stability. This suggests that the definition of K-stability may need to be edited to account for these limiting examples.