Image (category theory)

In category theory, a branch of mathematics, the image of a morphism is a generalization of the image of a function.

General Definition

Given a category $C$ and a morphism $f\colon X\to Y$ in $C$ , the image [1] of $f$ is a monomorphism $m\colon I\to Y$ satisfying the following universal property:

There exists a morphism $e\colon X\to I$ such that $f=m\,e$ .
For any object $I'$ with a morphism $e'\colon X\to I'$ and a monomorphism $m'\colon I'\to Y$ such that $f=m'\,e'$ , there exists a unique morphism $v\colon I\to I'$ such that $m=m'\,v$ .

Remarks:

such a factorization does not necessarily exist.
$e$ is unique by definition of $m$ monic.
$m'e'=f=me=m've\implies e'=ve$ by $m$ monic.
$v$ is monic.
$m=m'\,v$ already implies that $v$ is unique.

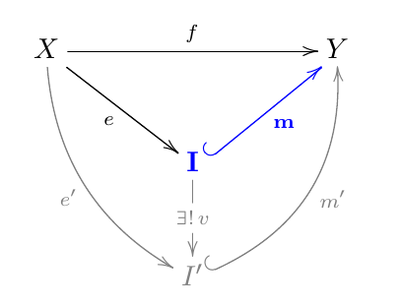
The image of $f$ is often denoted by ${\text{Im}}f$ or ${\text{Im}}(f)$ .

Proposition: If $C$ has all equalizers then the $e$ in the factorization $f=m\,e$ of (1) is an epimorphism. [2]

Proof

Let $\alpha ,\,\beta$ be such that $\alpha \,e=\beta \,e$ , one needs to show that $\alpha =\beta$ . Since the equalizer of $(\alpha ,\beta )$ exists, $e$ factorizes as $e=q\,e'$ with $q$ monic. But then $f=(m\,q)\,e'$ is a factorization of $f$ with $(m\,q)$ monomorphism. Hence by the universal property of the image there exists a unique arrow $v:I\to Eq_{\alpha ,\beta }$ such that $m=m\,q\,v$ and since $m$ is monic ${\text{id}}_{I}=q\,v$ . Furthermore, one has $m\,q=(mqv)\,q$ and by the monomorphism property of $mq$ one obtains ${\text{id}}_{Eq_{\alpha ,\beta }}=v\,q$ .

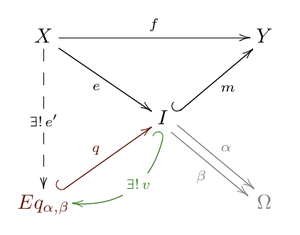
This means that $I\equiv Eq_{\alpha ,\beta }$ and thus that ${\text{id}}_{I}=q\,v$ equalizes $(\alpha ,\beta )$ , whence $\alpha =\beta$ .

Second definition

In a category $C$ with all finite limits and colimits, the image is defined as the equalizer $(Im,m)$ of the so-called cokernel pair $(Y\sqcup _{X}Y,i_{1},i_{2})$ .[3]

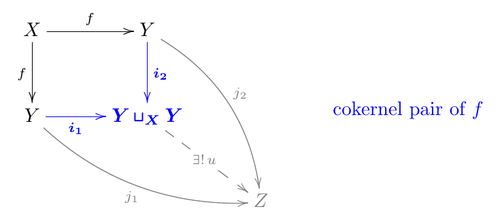
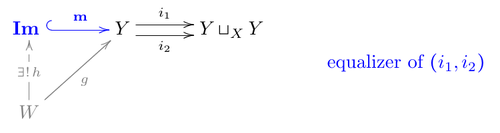
Remarks:

Finite bicompleteness of the category ensures that pushouts and equalizers exist.
$(Im,m)$ can be called regular image as $m$ is a regular monomorphism, i.e. the equalizer of a pair of morphism. (Recall also that an equalizer is automatically a monomorphism).
In an abelian category, the cokernel pair property can be written $i_{1}\,f=i_{2}\,f\ \Leftrightarrow \ (i_{1}-i_{2})\,f=0=0\,f$ and the equalizer condition $i_{1}\,m=i_{2}\,m\ \Leftrightarrow \ (i_{1}-i_{2})\,m=0\,m$ . Moreover, all monomorphisms are regular.

Theorem — If $f$ always factorizes through regular monomorphisms, then the two definitions coincide.

Proof

First definition implies the second: Assume that (1) holds with $m$ regular monomorphism.

Equalization: one needs to show that $i_{1}\,m=i_{2}\,m$ . As the cokernel pair of $f,\ i_{1}\,f=i_{2}\,f$ and by previous proposition, since $C$ has all equalizers, the arrow $e$ in the factorization $f=m\,e$ is an epimorphism, hence $i_{1}\,f=i_{2}\,f\ \Rightarrow \ i_{1}\,m=i_{2}\,m$ .
Universality: in a category with all colimits (or at least all pushouts) $m$ itself admits a cokernel pair $(Y\sqcup _{I}Y,c_{1},c_{2})$

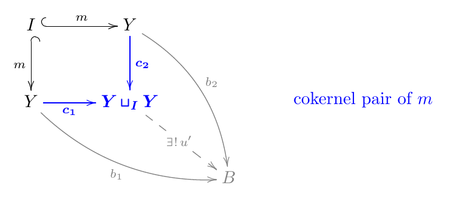
Moreover, as a regular monomorphism,

(I,m)

is the equalizer of a pair of morphisms

b_{1},b_{2}:Y\longrightarrow B

but we claim here that it is also the equalizer of

c_{1},c_{2}:Y\longrightarrow Y\sqcup _{I}Y

.

Indeed, by construction

b_{1}\,m=b_{2}\,m

thus the "cokernel pair" diagram for

m

yields a unique morphism

u':Y\sqcup _{I}Y\longrightarrow B

such that

b_{1}=u'\,c_{1},\ b_{2}=u'\,c_{2}

. Now, a map

m':I'\longrightarrow Y

which equalizes

(c_{1},c_{2})

also satisfies

b_{1}\,m'=u'\,c_{1}\,m'=u'\,c_{2}\,m'=b_{2}\,m'

, hence by the equalizer diagram for

(b_{1},b_{2})

, there exists a unique map

h':I'\to I

such that

m'=m\,h'

.

Finally, use the cokernel pair diagram (of

f

) with

j_{1}:=c_{1},\ j_{2}:=c_{2},\ Z:=Y\sqcup _{I}Y

: there exists a unique

u:Y\sqcup _{X}Y\longrightarrow Y\sqcup _{I}Y

such that

c_{1}=u\,i_{1},\ c_{2}=u\,i_{2}

. Therefore, any map

g

which equalizes

(i_{1},i_{2})

also equalizes

(c_{1},c_{2})

and thus uniquely factorizes as

g=m\,h'

. This exactly means that

(I,m)

is the equalizer of

(i_{1},i_{2})

.

Second definition implies the first:

Factorization: taking $m':=f$ in the equalizer diagram ( $m'$ corresponds to $g$ ), one obtains the factorization $f=m\,h$ .
Universality: let $f=m'\,e'$ be a factorization with $m'$ regular monomorphism, i.e. the equalizer of some pair $(d_{1},d_{2})$ .

Then

d_{1}\,m'=d_{2}\,m'\ \Rightarrow \ d_{1}\,f=d_{1}\,m'\,e=d_{2}\,m'\,e=d_{2}\,f

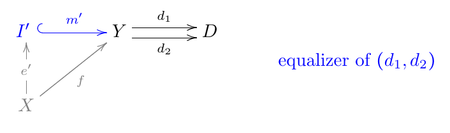
so that by the "cokernel pair" diagram (of

f

), with

j_{1}:=d_{1},\ j_{2}:=d_{2},\ Z:=D

, there exists a unique

u'':Y\sqcup _{X}Y\longrightarrow D

such that

d_{1}=u''\,i_{1},\ d_{2}=u''\,i_{2}

.

Now, from

i_{1}\,m=i_{2}\,m

(m from the equalizer of (i₁, i₂) diagram), one obtains

d_{1}\,m=u''\,i_{1}\,m=u''\,i_{2}\,m=d_{2}\,m

, hence by the universality in the (equalizer of (d₁, d₂) diagram, with f replaced by m), there exists a unique

v:Im\longrightarrow I'

such that

m=m'\,v

.

Examples

In the category of sets the image of a morphism $f\colon X\to Y$ is the inclusion from the ordinary image $\{f(x)~|~x\in X\}$ to $Y$ . In many concrete categories such as groups, abelian groups and (left- or right) modules, the image of a morphism is the image of the correspondent morphism in the category of sets.

In any normal category with a zero object and kernels and cokernels for every morphism, the image of a morphism $f$ can be expressed as follows:

im f = ker coker f

In an abelian category (which is in particular binormal), if f is a monomorphism then f = ker coker f, and so f = im f.

References

Mitchell, Barry (1965), Theory of categories, Pure and applied mathematics, 17, Academic Press, ISBN 978-0-124-99250-4, MR 0202787 Section I.10 p.12
Mitchell, Barry (1965), Theory of categories, Pure and applied mathematics, 17, Academic Press, ISBN 978-0-124-99250-4, MR 0202787 Proposition 10.1 p.12
Kashiwara, Masaki; Schapira, Pierre (2006), "Categories and Sheaves", Grundlehren der Mathematischen Wissenschaften, 332, Berlin Heidelberg: Springer, pp. 113–114 Definition 5.1.1

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Mitchell, Barry (1965), Theory of categories, Pure and applied mathematics, 17, Academic Press, ISBN 978-0-124-99250-4, MR 0202787 Section I.10 p.12

[2] Mitchell, Barry (1965), Theory of categories, Pure and applied mathematics, 17, Academic Press, ISBN 978-0-124-99250-4, MR 0202787 Proposition 10.1 p.12

[3] Kashiwara, Masaki; Schapira, Pierre (2006), "Categories and Sheaves", Grundlehren der Mathematischen Wissenschaften, 332, Berlin Heidelberg: Springer, pp. 113–114 Definition 5.1.1

Image (category theory)

General Definition

Second definition

Examples

See also

References