Euler's theorem in geometry

Proof of Euler's theorem in geometry

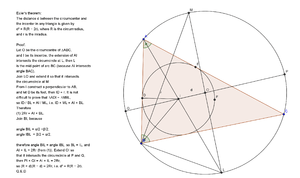
Letting O be the circumcentre of triangle ABC, and I be its incentre, the extension of AI intersects the circumcircle at L. Then L is the midpoint of arc BC. Join LO and extend it so that it intersects the circumcircle at M. From I construct a perpendicular to AB, and let D be its foot, so ID = r. It is not difficult to prove that triangle ADI is similar to triangle MBL, so ID / BL = AI / ML, i.e. ID × ML = AI × BL. Therefore 2Rr = AI × BL. Join BI. Because

∠ BIL = ∠ A / 2 + ∠ ABC / 2,

∠ IBL = ∠ ABC / 2 + ∠ CBL = ∠ ABC / 2 + ∠ A / 2,

we have ∠ BIL = ∠ IBL, so BL = IL, and AI × IL = 2Rr. Extend OI so that it intersects the circumcircle at P and Q; then PI × QI = AI × IL = 2Rr, so (R + d)(R − d) = 2Rr, i.e. d² = R(R − 2r).

A stronger version[7]^{:p. 198} is

${\displaystyle {\frac {R}{r}}\geq {\frac {abc+a^{3}+b^{3}+c^{3}}{2abc}}\geq {\frac {a}{b}}+{\frac {b}{c}}+{\frac {c}{a}}-1\geq {\frac {2}{3}}\left({\frac {a}{b}}+{\frac {b}{c}}+{\frac {c}{a}}\right)\geq 2,}$

where a, b, c are the sidelengths of the triangle.

If ${\displaystyle r_{a}}$ and ${\displaystyle d_{a}}$ denote respectively the radius of the escribed circle opposite to the vertex ${\displaystyle A}$ and the distance between its centre and the centre of the circumscribed circle, then ${\displaystyle d_{a}^{2}=R(R+2r_{a})}$.

Euler's inequality, in the form stating that, for all triangles inscribed in a given circle, the maximum of the radius of the inscribed circle is reached for the equilateral triangle and only for it, is valid in absolute geometry.[8]

• Fuss' theorem for the relation among the same three variables in bicentric quadrilaterals
• Poncelet's closure theorem, showing that there is an infinity of triangles with the same two circles (and therefore the same R, r, and d)
• List of triangle inequalities

Wikimedia Commons has media related to Euler's theorem in geometry.

• Weisstein, Eric W. "Euler Triangle Formula". MathWorld.